Irudi (matematika)

Baldin eta ${\displaystyle x}$ ${\displaystyle X}$-ren elementua bada, orduan ${\displaystyle x}$-ren irudia ${\displaystyle f}$-n, ${\displaystyle f(x)}$ deitua, ${\displaystyle x}$ ordezkatzean ${\displaystyle f}$-k hartzen duen balioa da. ${\displaystyle f(x)}$ ${\displaystyle x}$-rako ${\displaystyle f}$-ren irteera gisa ezagutzen da.

${\displaystyle y}$ emanda, ${\displaystyle f}$ funtzioak "${\displaystyle y}$-ren balioa hartzen duela" esaten da baldin eta existiten bada ${\displaystyle x}$ bat funtzioaren eremuan non ${\displaystyle f(x)=y}$ den. Era berean, ${\displaystyle S}$ multzo bat emanda, ${\displaystyle f}$-k "${\displaystyle S}$-ren balioa hartzen duela" esaten da baldin eta existiten bada ${\displaystyle x}$ bat funtzioaren eremuan non ${\displaystyle f(x)\in S}$. Aldiz, "${\displaystyle f}$-k ${\displaystyle S}$-ren balio guztiak hartzen dituela" esaten da edozein ${\displaystyle x}$ ${\displaystyle f}$-ren eremuan ${\displaystyle f(x)\in S}$ bada.

${\displaystyle A\subseteq X}$ azpimultzoaren irudia ${\displaystyle f}$-n, ${\displaystyle f(A)}$ deitua, ${\displaystyle Y}$-ren azpimultzoa da multzoak osatzeko notazioa erabiliz definitu daitekeena: [1][2]

${\displaystyle f(A)=\{f(x):x\in A\}}$

Nahasteko arriskurik ez dagoenean, ${\displaystyle f[A]}$ honela idazten da: ${\displaystyle f(A)}$. Konbentzio hori komuna da; aurreikusitako esanahia testuingurutik ondorioztatu behar da. Horren ondorioz, ${\displaystyle f[\cdot ]}$ funtzio bat da zeinen eremua ${\displaystyle X}$-ren potentzia-multzoa den eta koeremua ${\displaystyle Y}$-ren potentzia-multzoa.

Funtzio baten irudia bere domeinu osoaren irudia da, funtzioaren heina ere deitua.[3] Erabilera hori saihestu egin behar da, "hein" hitza ere ${\displaystyle f}$-ren koeremua adierazteko erabiltzen baita.

${\displaystyle R}$ erlazio bitar arbitrarioa bada ${\displaystyle X\times Y}$-n, orduan ${\displaystyle \{y\in Y:xRy\ non\ x\in X\}}$ multzoari ${\displaystyle R}$-ren irudia (edo heina) deitzen zaio. Era berean, ${\displaystyle \{x\in X:xRy\ non\ y\in Y\}}$ multzoari ${\displaystyle R}$-ren eremua deritzo.

• ${\displaystyle f^{\rightarrow }:P(X)\rightarrow P(Y)}$, ${\displaystyle f^{\rightarrow }=\{f(a)\mid a\in A\}}$
• ${\displaystyle f^{\leftarrow }:P(Y)\rightarrow P(X)}$, ${\displaystyle f^{\leftarrow }=\{a\in X\mid f(a)\in B\}}$

• ${\displaystyle f_{\star }:P(X)\rightarrow P(Y)}$, ${\displaystyle f^{\rightarrow }}$-ren ordez
• ${\displaystyle f^{\star }:P(Y)\rightarrow P(X)}$, ${\displaystyle f^{\leftarrow }}$-ren ordez

• ${\displaystyle f[A]}$-ren ordez ${\displaystyle f''A}$ ere erabiltzen da. [6][7]
• Zenbait testuk ${\displaystyle f}$-ren irudia ${\displaystyle f}$-ren heina deitzen dute, baina erabilera hori saihestu egin behar da, “hein” hitza ere erabili ohi baita ${\displaystyle f}$-ren koeremua adierazteko.

${\displaystyle f:X\longrightarrow Y}$ edozein funtziorako eta ${\displaystyle A\subseteq X}$ eta ${\displaystyle B\subseteq Y}$ azpimultzo guztietarako, propietate hauek betetzen dira:

Irudia	Aurreirudia
${\displaystyle f(X)\in Y}$	${\displaystyle f^{-1}(Y)=X}$
${\displaystyle f(f^{-1}(Y))=f(X)}$	${\displaystyle f(f^{-1}(X))=X}$
${\displaystyle f(f^{-1}(B))\subseteq B}$ (berdin ${\displaystyle f}$ supraiektiboa bada)[8][9]	${\displaystyle f(f^{-1}(A))\supseteq A}$(berdin ${\displaystyle f}$ injektiboa bada)[8][9]
${\displaystyle f(f^{-1}(B))=B\cap f(X)}$	${\displaystyle (f\mid _{A})^{-1}(B)=A\cap f^{-1}(B)}$
${\displaystyle f(f^{-1}(f(A)))=f(A)}$	${\displaystyle f^{-1}(f(f^{-1}(B)))=f^{-1}(B)}$
${\displaystyle f(A)=\emptyset }$ baldin eta soilik baldin ${\displaystyle A=\emptyset }$	${\displaystyle f^{-1}(B)=\emptyset }$ baldin eta soilik baldin ${\displaystyle B\subseteq Y\ \setminus f(X)}$
${\displaystyle f(A)\supseteq B}$ baldin eta soilik baldin existitzen bada ${\displaystyle C\subseteq A}$ non ${\displaystyle f(C)=B}$ den	${\displaystyle f^{-1}(B)\supseteq A}$ baldin eta soilik baldin ${\displaystyle f(A)\supseteq B}$
${\displaystyle f(A)\supseteq f(X\backslash A)}$ baldin eta soilik baldin ${\displaystyle f(A)=f(X)}$	${\displaystyle f^{-1}(B)\supseteq f^{-1}(Y\backslash B)}$ baldin eta soilik baldin ${\displaystyle f^{-1}(B)=X}$
${\displaystyle f(X\backslash A)\supseteq f(X)\setminus f(A)}$	${\displaystyle f^{-1}(Y\backslash B)=X\setminus f^{-1}(B)}$[8]
${\displaystyle f(A\ \cup f^{-1}(B))\subseteq f(A)\cup B}$	${\displaystyle f^{-1}(f(A)\cup B)\supseteq A\cup f^{-1}(B)}$
${\displaystyle f(A\ \cap f^{-1}(B))=f(A)\cap B}$	${\displaystyle f^{-1}(f(A)\cap B)\supseteq A\cap f^{-1}(B)}$

Horrez gain:

• ${\displaystyle f(A)\cap B=\emptyset }$ baldin eta soilik baldin ${\displaystyle A\cap f^{-1}(B)=\emptyset }$

${\displaystyle f:X\longrightarrow Y}$ eta ${\displaystyle g:Y\longrightarrow Z}$ funtzioetarako ${\displaystyle A\subseteq X}$ eta ${\displaystyle C\subseteq Z}$ azpimultzoekin, ondorengo propietateak betetzen dira:

• ${\displaystyle (g\circ f)(A)=g(f(A))}$
• ${\displaystyle (g\circ f)^{-1}(C)=f^{-1}(g^{-1}(C))}$

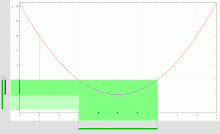
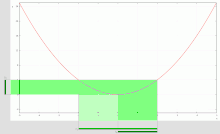
Zenbaki errealetan oinarritutako kontraadibideak ${\displaystyle \mathbb {R} }$, ${\displaystyle f:\mathbb {R} \rightarrow \mathbb {R} }$ honek definituta: ${\displaystyle f(x)=x^{2}}$, berdintasuna lege batzuetan betetzen ez dela erakusten dutenak:
Berdinak ez diren multzoak erakusten dituen irudia: ${\displaystyle f(A\cap B)\subsetneq f(A)\cap f(B)}$. ${\displaystyle A=[-4,2]}$ eta ${\displaystyle B=[-2,4]}$ multzoa urdinez agertzen dira ${\displaystyle x}$ ardatzaren azpian, haien ebakidura ${\displaystyle A_{3}=[-2,2]}$ berdez agertzen da.	${\displaystyle f(f^{-1}(B_{3}))\subsetneq B_{3}}$	${\displaystyle f^{-1}(f(A_{4}))\supsetneq A_{4}}$