Hookeren elastikotasun legea

Lege horrek Robert Hooke fisikari ingelesaren izena du, Isaac Newtonen garaikidea eta arkitekturaran ekarpen oparoak egin zituena. Norbaitek bere aurkikuntza ebatsiko ote zion beldur, Hookek anagrama famatu baten moduan argitaratu zuen, ceiiinosssttuv, eta bi urte geroago azaldu zuen bere edukia. Anagrama latinezko Ut tensio sic vis esaldiarena zen ("nolako luzapena, halako indarra").

Hookeren legeak malgukiari indar bat aplikatzean luzapena zenbatekoa izango den zehazten du.

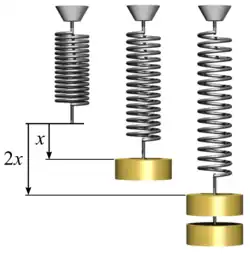
Hookeren legea matematikoki irudikatzeko modurik ohikoena malgukiaren ekuazioaren bidezkoa da. Ekuazio horretan, malgukiak jasandako ${\displaystyle \delta }$ elongazioa eta honek egindako ${\displaystyle F}$ indarra zuzenki proportzionalak dira. Bestalde, akzio-erreakzioaren legearen arabera, malgukiak jasandako indarra eta egindakoa kontrako zentzua duten bi indar berdin dira.

${\displaystyle F=-k\ \delta }$

non ${\displaystyle F}$ malgukiak egiten duen indarra baita, ${\displaystyle \delta }$ elongazioa eta ${\displaystyle k}$ berriz malgukiaren konstante elastikoa edo zurruntasuna.

Malgukiaren luzapenari lotutako deformazio-energia edo energia potentzial elastikoa (${\displaystyle U_{k}}$) ekuazio honek ematen du:

${\displaystyle U_{k}={\frac {1}{2}}\ k\ {\delta }^{2}}$

Garrantzitsua da nabarmentzea lehen zehaztutako ${\displaystyle k}$ zurruntasuna malgukiaren luzeraren eta haren eraketaren araberakoa dela. Malgukiaren konstante intrintsekoa ere defini daiteke, malguki horren luzerarekiko independentea, eta, hala, malguki bat osatzen duen lege diferentziala ezarriko dugu. ${\displaystyle k}$ malgukiaren zurruntasuna jatorrizko luzera osoarekin biderkatuz, eta biderkadurari ${\displaystyle k_{i}}$ (${\displaystyle k}$ intrintsekoa) deituz, honakoa lortzen da:

${\displaystyle k={\frac {k_{i}}{L}}}$

Mutur batetik x distantziara dagoen malgukiaren sekzio bateko tentsioa ${\displaystyle F(x)}$ izenda daiteke (x koordenatuen jatorritzat hartuko dugu, deformaziorik gabeko egoeran), eta ${\displaystyle k_{\Delta x}}$ malguki zati baten zurruntasuna, ${\displaystyle \Delta x}$ malguki zati horren luzera eta ${\displaystyle \delta _{\Delta x}}$ zati horrek jasan duen elongazioa. Horrela, zehatz daiteke:

${\displaystyle F(x)=-k_{\Delta x}\ \delta _{\Delta x}=-k_{i}{\frac {\delta _{\Delta x}}{\Delta x}}}$

Limiteak hartuz:

${\displaystyle F(x)=-k_{i}{\frac {{\delta }_{dx}}{dx}}}$

Hots:

${\displaystyle F(x)=-k_{i}{\frac {d{\delta }}{dx}}=-(A\ E){\frac {d\delta }{dx}}}$