Hiperbola
Hiperbola fokuak deritzen bi puntu finkoetarainoko distantzien kendura konstantea duten planoko puntu guztien leku geometrikoa da. Kono bati konoaren oinarriarekiko ebakidura elkartzut bat egitean agertzen den irudi geometrikoa da.
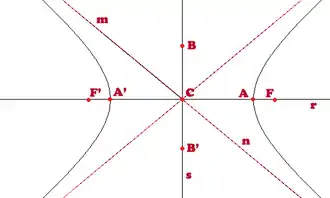

Hiperbola baten elementuak
- Fokuak: eta puntuak.
- Simetria-ardatzak: Bi fokuetatik puntuetatik igarotzen den zuzena eta horren zuzen erdibitzailea.
- Zentroa: puntua, hau da, simetria-ardatzen ebaki-puntua.
- Erpin errealak: eta puntuak, hau da, hiperbolaren era zuzenaren arteko ebaki-puntuak.
- Erpin irudikariak: eta puntuak, hau da, zentroa puntuan izanik, erradioko zirkunferentziaren eta zuzenaren arteko ebaki-puntuak.
- Ardatz erreala: segmentua.
- Ardatz irudikaria: segmentua.
- Foku-distantzia: segmentuaren luzera.
- Asintotak: eta zuzenak.
non,
Exzentrikotasuna
Hiperbolaren exzentrikotasuna, foku-distantzia erdiaren eta ardatz nagusiaren erdiaren arteko zatidura da. Hiperbola baten exzentrikotasuna beti 1 da, c = a delako.
Ekuazioak
- Hiperbola X ardatzean orientatuta badago eta zentrua (0,0) puntuan ez badago:
- Hiperbola X ardatzean orientatuta badago eta zentrua (0,0) bada:
- Hiperbola Y ardatzean orientatuta badago eta zentrua (0,0) puntuan ez badago:
- Hiperbola Y ardatzean orientatuta badago eta zentrua (0,0) bada:
Kanpo estekak
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.