Gas

Boyle-Mariotteren legea gas idealen legeetako bat da, prozesu isotermoa aztertzen duena hain zuzen ere. Robert Boylek Oxforden (1664) eta Edme Mariottek Parisen (1676), bakoitzak bere aldetik, aurkituriko legea da.

Legeak dioenez, gas baten sartu-irtenik gabe gasaren tenperatura konstante mantentzen bada gas honen gaineko presioa eta gasaren bolumena alderantziz proportzionalak dira. Hau da:

${\displaystyle P_{1}V_{1}=P_{2}V_{2}\,}$

Ikurrak:

${\displaystyle P_{1}\,}$= Hasierako presioa (atm)

${\displaystyle V_{1}\,}$= Hasierako bolumena (litro)

${\displaystyle P_{2}\,}$= Amaierako presioa (atm)

${\displaystyle V_{2}\,}$= Amaierako bolumena (litro)

Tenperatura konstante mantenduz bolumena eta presioaren arteko erlazioa azaltzen duen saiakuntzaren animazioa

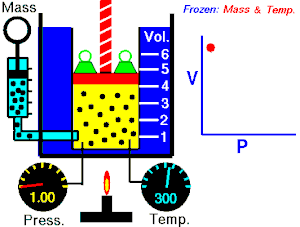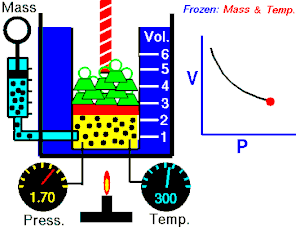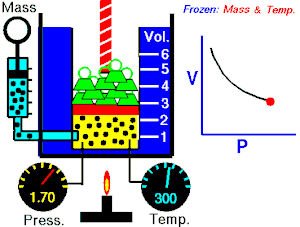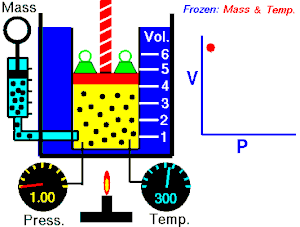
Hau da Boylek egin zuen esperimentua. Tenperatura konstante mantenduz, presioa handitu ahala bolumena jeisten zela ikusi zuen, baina, beti ere, bien arteko biderkaketa konstante mantentzen zen. Horretarako, ontzi batean, gasa sartu zuten, eta, goiko aldean, enbolo batekin hermetikoki itxi. Enboloan pisua jarriz, hura jeitsi eta bolumena txikitzen zenean, ontzi barruko gasaren presioa igo egiten zen; aldiz, enboloa jasoz, presioa txikitu egiten zen bolumena handitzean.

Bolumena txikitzerakoan, gas molekulek toki gutxiago dute mugitzeko, eta maizago jotzen dituzte ontziaren hormak. Aldiz, bolumena handitzerakoan, molekulek toki gehiago dute, eta hormen kontrako talkak gutxiagotu egiten dira.

Charlesen legea Jacques Charles fisikari frantziarrak 1787an azaldutako legea da, baina ez zen ezagutarazi 1802 arte, Gay-Lussacek beronen berri eman zuen arte. John Dalton kimikari ingelesak, bere aldetik, lege bera lortu zuen 1801ean (oraindik, Charlesen legea publikatu gabe zegoen), baina Charlesek, lehenago aurkitzeaz gain, askoz hobeto dokumentatua zuenez beronen izena darama legeak.[8].

Legeak dioenez, gas baten sartu-irtenik gabe gasaren presioa konstante mantentzen bada, gas horren bolumena eta gasaren tenperatura zuzenki proportzionalak dira. Hau da:

${\displaystyle {\frac {V_{1}}{T_{1}}}={\frac {V_{2}}{T_{2}}}}$

Ikurrak:

${\displaystyle V_{1}\,}$= Hasierako bolumena (litro)

${\displaystyle T_{1}\,}$= Hasierako tenperatura (ºK)

${\displaystyle V_{2}\,}$= Amaierako bolumena (litro)

${\displaystyle T_{2}\,}$= Amaierako tenperatura (ºK)

Presioa konstante mantenduz bolumena eta tenperaturaren erlazioa azaltzen duen saiakuntzaren animazioa

Charlesek, ontzi batean, gas bat sartu zuen goian enbolo batek hermetikoki ontzia ixten zuelarik. Orduan, ontzia berotzerakoan enboloa igo egiten zela (bolumena handitzearen ondorioz) ikusi zuen, eta berriz hozten uzterakoan enboloa jeisti egiten zela.

Gasa berotzerakoan, gasaren molekulek abiadura handiagotzen dute, eta hormen kontrako talkak ugaritzen dira ontziaren berneko presioa handituz. Enboloak gora jotzen du presio atmosferikoarekin berdintzen den arte.

Gas idealen legea ulertzeko bideoa.

---

Bideo hau Jakindun elkarteak egin du. Gehiago dituzu eskuragarri euren gunean. Bideoak dituzten artikulu guztiak ikus ditzakezu hemen.

Gay-Lussacen legea Louis Joseph Gay-Lussac kimikari frantziarrak 1805ean azaldutako legea da. Gas idealen legeetako bat da.[9]:

Legeak dioenez, gas baten sartu-irtenik gabe gasaren bolumena konstante mantentzen bada, gas horren presioa eta gasaren tenperatura zuzenki proportzionalak dira. Hau da:

${\displaystyle {\frac {P_{1}}{T_{1}}}={\frac {P_{2}}{T_{2}}}}$

Ikurrak:

${\displaystyle P_{1}\,}$= Hasierako presioa (atm)

${\displaystyle T_{1}\,}$= Hasierako tenperatura (ºK)

${\displaystyle P_{2}\,}$= Amaierako presioa (atm)

${\displaystyle T_{2}\,}$= Amaierako tenperatura (ºK)

Gay-Lussacek gas bat sartu zuen ontzi itxi batean. Ontziaren azpian, pizgailua jarriz gasa berotu, eta ontziaren hormen kontrako presioa handitu zela ikusi zuen. Bero iturria itzaltzerakoan, presioa jeisten joan zen hasierako egoerara iritsi arte.

Gasaren molekulak berotzerakoan azkarrago mugitzen dira, eta, beraz, hormen aurka egiten dituzten talkak ugaritu egiten dira. Aldiz, tenperatura jeistean, molekulak moteldu egiten dira, eta hormen aurkako talkak, gutxitu.

Gasen lege orokorrak presio, tenperatura eta bolumen aldagaiekiko hauen portamoldea argitzen du. Honela, gas masa konstante batean, aldagai hauen arteko erlazioa hurrengo berdinketak ezartzen du:

${\displaystyle {\frac {P_{1}V_{1}}{T_{1}}}={\frac {P_{2}V_{2}}{T_{2}}}}$

Txantiloi:Sakontzeki Gas idealen legeak gas idealek presio, bolumen eta tenperaturaren artean dituzten erlazioak azaltzen dituzten legeak dira.

Legeak argitzen duenez, aldagai osagarrien doitze bat eragingo du hasierako egoera betako (1) gas batean aldagai baten magnitude bat aldatzean berdintasuna mantentzeko amaiera egoeran (2).

Tenperatura konstante mantentzen bada (T₁=T₂), posible da berau ekuaziotik kentzea. Beraz berdintasuna presio eta bolumen arteko aldaketen bidez mantentzen da.

Boyleren lan-tresna

Émile Clapeyronek azaldu zuen lehenengo aldiz, 1834ean. Aurretik Boyle, Mariotte, Charles eta Gay-Lussacek eginiko lanak bateratu ostean lortu zuen ekuazioa sortzea. Ekuazioa honako hau da:

${\displaystyle P\cdot V=n\cdot R\cdot T\,\!}$

Ikurrak:

• ${\displaystyle P\!}$ = Presio absolutua (atmosferatan neurtua)
• ${\displaystyle V\!}$ = Bolumena (litrotan)
• ${\displaystyle n\!}$ = Gas molak
• ${\displaystyle R\!}$ = gas idealen konstante unibertsala (0'082)
• ${\displaystyle T\!}$ = Tenperatura absolutua (Kelvinetan)

Legeak argitzen duenez, aldagai osagarrien doitze bat eragingo du hasierako egoera betako (1) gas batean aldagai baten magnitude bat aldatzean berdintasuna mantentzeko amaiera egoeran (2).

Tenperatura konstante mantentzen bada (T₁=T₂), posible da berau ekuaziotik kentzea. Beraz berdintasuna presio eta bolumen arteko aldaketen bidez mantentzen da.

Daltonen legeak gas nahasketa baten guztirako presioa gas bakoitzak bolumen osoa okupatuko balitz eragiten dituzten presioen batzea dela argitzen du.

${\displaystyle P_{total}=\sum _{i=1}^{n}{p_{i}}}$       or      ${\displaystyle P_{total}=p_{1}+p_{2}+\cdots +p_{n}}$

Lege hau presio partzialen legea bezala ere ezagutzen da, gas batek X presioan batean duen presio partziala nahasketan dagoen gasen proportzioarekin zuzenki proportzionala baita.

Hau da, gas nahasketa batean osagai batek P presioan nahasketaren bolumenaren %20 betetzen badu, osagai horrek 0,2 Pko presio partzial bat du.

Henry-ren legea: Disoluzio diluitu ideal batean, solutu baten lurrunaren presioa ematen digu. Disolbatzailearentzat Roult-en legea erabiltzen jarraitzen da: PA=xAP∗A

Gas bat likido batekin harremanetan ipintzean, gasaren molekulak (bere energia termodinamikoa -presio eta tenperatura- dela eta) gas-likido interfasean sartu, eta haren barnean banatzen dira. Egoera horri gasen disoluzioa esaten zaio, hau da, gas-likido disoluzio baten eraketa. Gas bat fase likidoan disolbaturik dagoenean, gasaren kontzentrazioari, (c) esaten zaio fase gaseosoan dagoenean eta presio partzialarentzako (p) erabiltzen den bitartean. Bada, Henry-ren legeak, bi adierazpen erlazionatzeko, Henryren konstantea erabiltzen du, horrela desio den presioa kalkulatzea ahalbidetuz.

p = soluzioaren presio partziala c = soluzioaren kontzentrazioa k_H = Henry legearen konstantea.

Horretarako, disolbatzaile bat eta solutuak dituen disoluzio diluitu ideal bat dagoenean, solutuek gas fasean eragiten duen presioa kalkulatzen da.

• Behin oreka lortuta:

μi,l(T,P)=μi,v(T,P) (1)

• Potentzial kimikoak, bere baloreengatik ordezkatuz:

μ0i,l(T,P)+RTlnxi=μ0i,v(T)+RTlnPiP0 (2)

• Terminoak elkartuz eta propietate logaritmiko nepertarrak erabiliz:

μ0i,l(T,P)−μ0i,v(T)RT=lnPixiP0 (3)

• Bakanduz

P0eμ0i,l(T,P)−μ0i,v(T)RTKH=Pixi (4)

• KH Henry-ren konstantea

Pi=KHxi (5)

Henry legeak argitzen duenez, tenperatura jakin batean eta saturazioa egoeran, likido batean disolbatzen den gas kopurua gasak likidoaren azalean eragiten duen presioarekiko zuzenki proportzionala da.

Henry legean izendatzen duen saturazio kontzeptuak gasaren presioren (gas egoeran) eta bere tentsioaren (likido egoeran) dagoen orekaz ari da. Presioa tentsioa baino handiago denean, azpisaturazio egoera esaten zaio; berdinak direnean, saturazio esaten zaio, eta presioa disolbaturiko gasaren tentsioa baino txikiagoa denean, supersaturazioa esaten zaio. Azpisaturazioan dagoen likido batek gas egoerako gasa disolbatuko du oreka (saturazio) iritsi arte. Supersaturazio egoeran, disolbaturiko gasa botako du oreka (saturazio) egoerara iritsi arte.

Bi gasen arteko zabalkunde fenomenoa. Lege horrek gasak nahasteko abiadura argitzen du. Oinarrian, tenperatura eta presio egoera beretan, bi gasen arteko zabalkundea gasen masa molarren erro karratuarekiko alderantziz proportzionala dela dio.

${\displaystyle {{\mbox{v}}_{1} \over {\mbox{v}}_{2}}={\sqrt {d_{2} \over d_{1}}}}$

non:

v₁ = 1 gasaren zabalkunde abiadura

v₂ = 2 gasaren zabalkunde abiadura

d₁ = 1 gasaren dentsitatea

d₂ = 2 gasaren dentsitatea

Beste era batera esanda, tenperatura eta presio berean, molekula arinak dituen gas baten zabalkunde abiadura molekula astunak dituena baino handiago da.

Gas batek zuntz bat (edo ehun kapa bat) zeharkatzeko duen transferentzia tasa azaltzen du. Hura, ageriko superfiziearekiko eta bere bi egoeren arteko ezberdintasunarekiko, proportzionala da, eta, zuntz/ehunaren lodierarekiko, alderantziz proportzionala da. Zabalkunde abiadura, gainera, zabalkunde konstantearekiko (parte hartzen duten ehun eta gas bakoitzerako bakarra), proportzionala da.

Gas-partikulen ausazko higidurak gas baten hedapena eragiten du.

Higidura browniarra fluido batean esekitako partikulen ausazko mugimendua deskribatzeko erabiltzen den eredu matematikoa da. Gas-partikulen animazioak (partikula arrosak eta berdeak erabiliz) erakusten du portaera horrek gasen hedapena (entropia) eragiten duela. Gertakari horiek partikulen teoriaren bidez ere deskribatzen dira.

Banakako gas-partikulak (atomoak edo molekulak) behatzea egungo teknologiaren mugan (edo harantzago) dagoenez, kalkulu teorikoek bakarrik ematen dute horiek mugitzeko moduari buruzko iradokizuna, baina higidura browniarra ez bezalakoa da, higidura browniarrak arrastatze-indar leuna baitakar gas-molekula askoren marruskadura-indarraren ondorioz, gas-molekula batek (edo batzuek) partikularekin izandako talka bortitzen ondorioz puntuatua. Partikulak (normalean, milioika edo milaka milioi atomo ditu), horrela, ibilbide irregular batean mugitzen dira, baina ez gas molekula indibidual bat aztertuz gero espero litzatekeen bezain irregularra.

Gas bat konprimatzean, molekulen arteko indarrek, hala nola irudiaren ur-molekulen arteko hidrogeno-loturek, paper aktiboagoa izaten hasten dira.

Partikulen arteko une bateko atrakzioek edo aldaratzeek eragina dute gasaren dinamikan. Kimika fisikoan, molekulen arteko indarren izena Van der Waalsen indarra da. Indar horiek zeregin bat dute gas baten propietate fisikoak zehazteko, hala nola likatasun edo fluxu bolumetrikoa. Indar horiek, baldintza jakin batzuetan, alde batera uzten baditugu, gas erreal bat gas ideal bat balitz bezala tratatu ahal izango dugu, eta, horrela, gas idealen legea erabili ahal izango dugu. Gasekiko erlazio horiek behar bezala erabiltzeko, teoria zinetikora itzuli behar da. Gasaren partikulek karga magnetikoa edo molekulen arteko indarra dutenean, beste molekuletan duten eragina areagotu egiten da haien arteko espazioa murriztu ahala. Kargarik ez dagoenean, partikulen arteko espazioa puntu jakin batera behar adina murriztu denean, partikulen arteko talkak ezin dira saihestu tenperatura normal batean.

Gas baten partikulen arteko talka-kopurua handitzeko, beste bide bat litzateke gas-bolumen finko jakin bat berotzea, gainera, partikulen tenperatura handiagoa, beraz, talkak izateko probabilitate handiagoa. Horrek guztiak esan nahi du ekuazio ideal horiek arrazoizko emaitzak ematen dituztela presio edo tenperatura handiko kasuetan izan ezik (ionizazioa). Salbuespenezko baldintza horiek aukera ematen dute gasaren barruan energia transferitzeko, eta, hain zuzen ere, energiaren barne-transferentziarik ez egoteak ahalbidetzen du baldintza idealei buruz hitz egitea, energia-trukea sistemaren mugetan bakarrik gertatzen baita.

Gas errealek talka eta indar intermolekular horietako batzuk izaten dituzte, baina, estatistikoki gutxiesgarriak diren bitartean, ekuazio idealen emaitzak baliozkoak izaten jarraituko dute. Bestalde, gas baten partikulak elkarrengandik oso hurbil daudenez konprimatzen direnean, gasak likido baten antzekoago jokatzen du, eta energiaren barne-transferentziarik ezak baldintza idealei buruz hitz egitea ahalbidetzen digu, energia trukea sistemaren mugetan bakarrik gertatzen baita. Gas errealek talka eta molekula arteko indar horietako batzuk izaten dituzte, baina, estatistikoki gutxiesgarriak diren bitartean, ekuazio idealen emaitzak baliozkoak izaten jarraituko dute.

Tenperaturak eta presioak solidoengan eta likidoengan duten eragina oso txikia denez, likido edo solido baten konprimagarritasuna da: 10^-6 bar^-1 (1 bar=0,1 MPa), eta dilatazio-koefiziente termikoa da: 10^-5 K^-1.

Bestalde, presioak eta tenperaturak eragin handia dute gasen dentsitatean. Gas idealen legeak matematikoki deskribatzen du hiru magnitude hauen arteko erlazioa:

${\displaystyle \rho ={\frac {p\,M}{R\,T}}}$

non ${\displaystyle R\,}$ gas idealen konstantea, ${\displaystyle p\,}$ gasaren presioa, ${\displaystyle M\,}$ masa molarra eta ${\displaystyle T\,}$ tenperatura absolutua den.

Horrek dakar 300 K (27 °C) eta 1 atm-ko gas ideal batek bere dentsitatea bikoiztuko duela presioa 2 atm-ra igotzen bada tenperatura konstantea mantenduz edo, txandaka, tenperatura 150 K-ra jaisten bada presio konstantea mantenduz.

Teoria zinetikoaren esparruan, gas baten presioa gasaren molekulek edukiontziaren paretekin talka egiten duten indarren emaitza makroskopiko gisa azaltzen da. Presioa, beraz, gasaren propietate mikroskopikoei erreferentzia eginez defini daiteke.

Izan ere, N molekuladun gas ideal batentzat (bakoitza m masaduna eta v_rms batez besteko ausazko abiadura V bolumen kubiko bateko edukian), gasaren partikulek ontziaren paretekin talka egiten dute, modu estatistikoan kalkula daitekeen moduan talka bakoitzean paretekin trukatuz momentu lineal eta area unitateko indar garbi bat eginez; bada, hura da, gainazal solidoan, gasak eragindako presioa.

Presioa honela kalkula daiteke:

${\displaystyle P={Nmv_{rms}^{2} \over 3V}}$ (gas ideala)

Emaitza hori interesgarria eta esanguratsua da, ez bakarrik gas baten presioa kalkulatzeko modu bat eskaintzen duelako, baizik eta aldagai makroskopiko behagarri bat, presioa, molekula bidezko batez besteko energia zinetikoa, 1/2 mv _rms², zuzenean ikus ezin daitekeen magnitude mikroskopikoa delako. Kontuan izan ontziaren bolumenak eragindako presioaren emaitza jasotako gas-molekulen guztizko energia zinetikoaren bi heren dela.

Airearen konprimatasunaren faktoreak.

Termodinamikan ("Z") faktorea gas idealaren ekuazioa aldatzeko erabiltzen da gas errealen konprimagarritasun-efektuak kontuan hartzeko. Faktore horrek bolumen espezifiko errealen eta idealen arteko erlazioa adierazten du. Batzuetan, aldaketa-faktorea edo diseinu-helburuetarako gas idealen legearen tarte erabilgarria zabaltzeko zuzenketa esaten zaio. Normalean Z-ren balio hori unitatetik oso gertu dago. Konprimagarritasun-faktorearen irudiak, tenperatura oso hotzetan, Z nola aldatzen den erakusten du.

Fluidoen mekanikan, Reynolds zenbakia inertzia-indarren (v_sρ) eta indar likatsuen (μ/L) arteko erlazioa da. Zenbaki adimentsional garrantzitsuenetako bat da fluidoen dinamikan, eta, eskuarki, beste zenbaki adimentsional batzuekin batera, antzekotasun dinamikoa zehazteko irizpidea emateko erabiltzen da. Horrela, Reynolds zenbakiak modelaketaren emaitzen (diseinua) eta eskala handiko benetako baldintzen arteko lotura ematen du. Fluxua karakterizatzeko ere erabil daiteke[9].

1999ko irailaren 15ean, Juan Fernandez uharteditik gertu zegoen klima-patroi baten ikuspegi satelitala; hodei zurrunbilotsuen eredu bat ikusten da, Von Karmanen zurrunbiloen kalea izenekoa.

Likatasun edo biskositatea fluido guztiak duten propietate fisiko bat da, eta hori fluido batean aurkitzen diren eta abiadura ezberdinetan mugitzen diren partikulen arteko kolisioetatik sortzen da, mugimenduari erresistentzia indar bat sortuz teoria zinematikoaren arabera. Fluido bat tubo baten barnealdetik pasarazten denean, fluido horren partikulak azkarrago mugitzen dira tuboaren ardatzetik gertu eta geldoago tuboaren paretetatik gertu direnak. Horregatik, ezinbestekoa da indar ebakitzaileak existitzea marruskadura indarrak ezarritako erresistentzia indarrak gainditu eta fluidoa mugitu ahal izateko. Hori gertatuko ez balitz, ez litzateke mugimendurik existituko.

Fluidoen dinamikan, turbulentzia edo fluxu zurrunbilotsua fluxu-erregimen bat da, ezaugarri hauek dituena: une jakin bateko difusio txikia, konbekzio handia eta presio- eta abiadura-aldaketa espazial azkarrak. Zurrunbilotsuak ez diren fluxuei, fluxu laminar deitzen zaie. Fluxu bat laminarra edo zurrunbilotsua izan daiteke Reynolds zenbakiaren magnitude-ordena begiratuz.

Partikulak bere baitan mugitzen den objektu baten gainazalean itsasten dira. Partikula-geruza horri muga-geruza deitzen zaio. Objektuaren gainazalean, funtsean, estatikoa da gainazalaren marruskaduraren ondorioz. Objektua, bere muga-geruzarekin, objektuaren forma berria da, objektua hurbildu ahala gainerako molekulek ikusten dutena. Muga-geruza hori azaleratik bereiz daiteke funtsean azalera berri bat sortuz eta fluxuaren ibilbidea erabat aldatuz. Horren adibide klasikoa galeran sartzen den profil hegoarra da. Delta hegalaren irudiak argi eta garbi erakusten du muga-geruzaren lodiera, gasak eraso-ertzean zehar eskuinetik ezkerrera egiten duen heinean[9].

Askatasun graduen kopuru osoa infinitura hurbiltzen den heinean, sistema aniztasun handienari dagokion makroegoeran aurkituko da. Printzipio hori irudikatzeko, begiratu metalezko barra izoztu baten gainazaleko tenperatura. Gainazaleko tenperaturaren irudi termikoa erabiliz, behatu gainazaleko tenperaturaren banaketa. Tenperaturaren hasierako behaketa horrek mikroegoera adierazten du. Etorkizuneko uneren batean, gainazaleko tenperaturaren bigarren behaketa batek bigarren mikroegoera sortzen du. Behaketa-prozesu horrekin jarraitzean, litekeena da barraren gainazalaren historia termikoa ilustratzen duten mikroegoera batzuk sortzea. Mikroegoeren serie historiko horren karakterizazioa posible da guztiak multzo bakar batean arrakastaz sailkatzen dituen makroegoera aukeratuz.

Sistema baten energia-transferentzia amaitzen denean, egoera horri, oreka termodinamikoa esaten zaio. Oro har, baldintza horrek esan nahi du sistema eta inguruak tenperatura berean daudela, eta, beraz, beroa ez da jada haien artean transferitzen. Era berean, kanpoko indarrak orekatuta daudela (bolumena ez da aldatzen) eta sistemaren barruko erreakzio kimiko guztiak osatuta daudela esan nahi du. Sistemaren arabera, kronograma aldatu egiten da gertaera horietarako. Giro-tenperaturan urtzen den izotz edukiontzi batek orduak eramango ditu; erdieroaleetan, berriz, gailua piztuta egotetik itzalita egotera doan trantsizioan gertatzen den bero-transferentzia nanosegundo gutxi batzuen ordenakoa izan liteke.