Gamma funtzio
Matematikan, gamma funtzioa faktorial kontzeptua zenbaki erreal eta konplexuetara zabaltzen duen aplikazioa da.[1] Greziako gamma letra maiuskularen sinboloarekin adierazten da: .
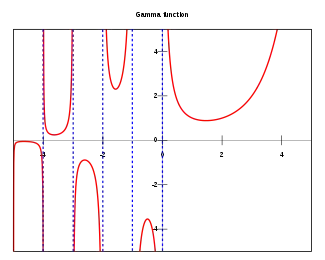
Notazioa Adrien-Marie Legendre-k proposatu zuen. Zenbaki konplexuaren zati erreala positiboa bada, integralak
guztiz bat egiten du; integral hori plano konplexu osora zabal daiteke, negatibo eta zero diren osoetan izan ezik. Orduan
funtzio horrek faktorearekin duen erlazioa erakusten digu. Hain zuzen, gamma funtzioak faktorialaren kontzeptu -ren edozein balio konplexutara hedatzen du. Gamma funtzioa probabilitate-banaketaren zenbait funtziotan agertzen da, eta, beraz, nahiko erabilia da bai probabilitatean, bai estatistikan, bai konbinatorian.
Hurbilketak
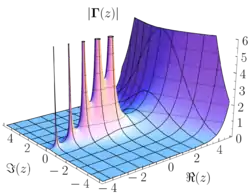
Gamma funtzioa zenbakiz kalkula daiteke zehaztasun arbitrarioarekin Stirling-en formula, Lanczos hurbilketa edo Spouge hurbilketa erabilita.[2]
1/24ren multiplo osoak diren argumentuetarako, gamma funtzioa azkar ebalua daiteke batezbesteko aritmetiko geometrikoen iterazioak erabiliz.
Gamma funtzioa eta faktoriala oso azkar hazten direnez, argumentu handietarako, konputazio-programa askok gamma funtzioaren logaritmoa itzultzen duten funtzioak dituzte[3]. Polikiago hazten da, eta konbinazio-kalkuluetan oso erabilgarria da, balio handiak biderkatu eta zatitzetik logaritmoak batu edo kentzera pasatzen baita.
Ikus, gainera
Erreferentziak
- «Zer da Gamma Funtzioa?» eu.eferrit.com (Noiz kontsultatua: 2022-11-28).
- «La función gamma» www.sc.ehu.es (Noiz kontsultatua: 2022-11-28).
- (Gaztelaniaz) ^DiAmOnD^. (2007-11-05). «La función Gamma: una generalización del factorial» Gaussianos (Noiz kontsultatua: 2022-11-28).