Funtzio baten irudikapen grafiko
Matematikan, funtzio baten portaera ikustea ahalbidetzen duen adierazpideari funtzio baten irudikapen grafikoa (funtzio baten grafikoa edo grafoa) deritzo. Edo, era formalagoan adierazita, izan bedi honako f funtzio hau:

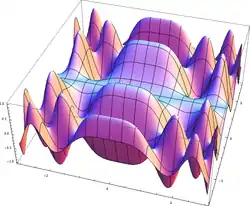
f funtzioaren irudikapen grafikoa (x,f(x)) bikote ordenatu guztien multzoaren irudikapen grafikoa da. Definizio-eremuaren eta irudiaren elementuen arteko korrespondentziaren bitartez irudikatzen da funtzioa (funtzioa injektiboa bada korrespondentzia hori bakarra izango da; hau da, x-ren balio bakoitzerako f(x) bakarra existituko da).
Era ez-anbiguoan irudika daitezkeen funtzio bakarrak aldagai bakarreko funtzioak dira, koordenatu kartesiarren sistema bat erabiliz, non abzisa bakoitzak definizio-eremuaren balio bat adierazten baitu eta ordenatuak abzisari dagokion balioa. Funtzioa jarraitua bada, orduan haren irudikapen grafikoa zuzen bat edo kurba bat izango da. Posible da bi aldagaiko funtzioak era bakar batean irudikatzea proiekzio geometriko baten bidez. Baina hiru aldagaitik gorako funtzioetan plano batekin egindako mozketak bakarrik bistara daitezke. Planoarekin mozketa egitean aldagai guztiak konstante mantentzen dira, bi izan ezik.
Definizio-eremua
Izan bedi f funtzio erreala, , f definituta dagoen balioei definizio-eremua deritze, , hots, baldin eta , zeinetarako .
tartearen araberako kasuak:
Funtzio baten analisia puntu batean
Izan bedi f non:
Funtzio hori puntuan aztertzean, honako kasu hauek agertzen dira:
Jarraitutasun-azterketa bat egiteko arau mnemotekniko on bat da ikustea ea arkatza altxatu behar den grafikoa irudikatzeko. Arkatza altxatu behar bada, funtzio ez-jarraitua dela edo etenune motaren bat dagoela esango dugu.
Jarraitutasun-puntuak
f funtzio erreala zehaztuta, non x erreal bakoitzari y erreal bat dagokion, y=f(x); honela adierazita:
x aldagaia a baliora hurbiltzen den heinean, y aldagaia L balio batera hurbiltzen da. L f-ren limitea dela esango dugu x a-ra hurbiltzen denean.
Funtzio batek puntu batean limitea badauka, limite horrek bakarra izan behar du (limitearen bakartasuna), eta limitearen balioak, existitzen bada, ez du zertan puntu horretako funtzioaren balioarekin kointziditu. Funtzio batek puntu batean limitea badauka eta limitearen balioa puntu horretako funtzioaren balioaren berdina bada, funtzioa jarraitua da puntu horretan:
Etenune-puntuak
Funtzio bat ez-jarraitua bada, ez-jarraitutasun hori definitzen duten puntuak etenune-puntuak dira, eta honela sailka daitezke:
Etenuneen adibideak

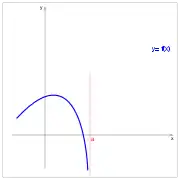


Bigarren mailakoa. Bigarren mailakoa. Bigarren mailakoa. Bigarren mailakoa.




Bigarren mailakoa. Bigarren mailakoa. Bigarren mailakoa. Bigarren mailakoa.

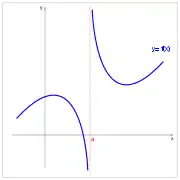


Asintotikoa. Asintotikoa. Asintotikoa. Asintotikoa.



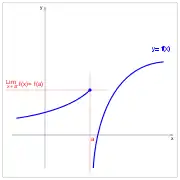
Jauzi infinitua. Jauzi infinitua. Jauzi infinitua. Jauzi infinitua.


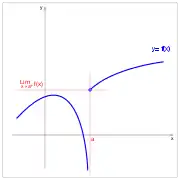

Jauzi infinitua. Jauzi infinitua. Jauzi infinitua. Jauzi infinitua.

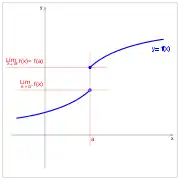

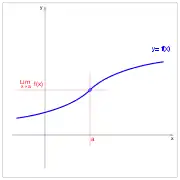
Jauzi finitua. Jauzi finitua. Jauzi finitua. Saihesgarria
Adibideak
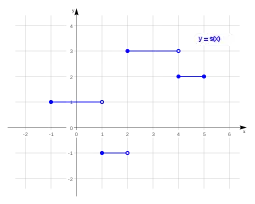
|
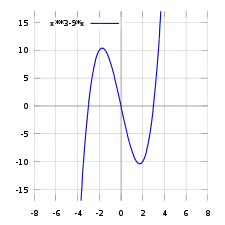 x3-9x funtzioaren grafikoa.
|
Aldagai bakarreko funtzioa irudikatzeko metodoa
Mendeko aldagai bat eta aldagai independente bat dituen funtzio bat irudika daiteke grafikoki, bi ardatz erabiliz: abzisa-ardatza eta ordenatu-ardatza. Normalean, mendeko aldagai gisa, erabiltzen da, abzisa-ardatzean, eta, aldagai independente gisa, , ordenatu-ardatzean.
f funtzio baten irudikapen grafikoa egiteko, honako urrats hauei jarrai diezaiekegu:
- Funtzioaren definizio eremua bilatu, Dom(f) edo Dom(f(x)).
- Aurkitu x-ren zein baliotarako f ez-jarraitua, hau da, zein puntutan ez dagoen definituta funtzioa. Puntu horietan, albo-limiteak kalkulatu. Modu honetan jakin dezakegu nola jokatzen duen f funtzioak x puntu horien inguruan.
- Bilatu funtzioaren limitea x infiniturantz eta minus infiniturantz jotzen duenean.
- Monotonia aztertu. f'(x) funtzioa f-ren lehenengo deribatua kalkulatu, eta zerora berdindu; horrela, funtzioaren mutur izan daitezkeen puntuak lortuko ditugu. Ondoren, f(x) funtzioa bi punturen artean gorakorra edo beherakorra den zehazten da, bi puntu horien artean dagoen balio bat, , hartuz eta f'() positiboa edo negatiboa den ikusiz (gorakorra edo beherakorra hurrenez hurren).
- f-ren kurbadura aztertu. f"(x) funtzioa f-ren bigarren deribatua kalkulatu, eta zerora berdindu; horrela, funtzioaren inflexio-puntuak izan daitezkeen puntuak lortuko ditugu. Lehen bezala, bi punturen artean balio bat, , hartu eta f"()-ren zeinua aztertu; arau honen arabera:
- Negatiboa bada f ganbila da.
- Positiboa bada f ahurra da.
 Ariketak
Ariketak
- Funtzioak
- Funtzio linealak ezagutzen.
- Funtzio linealaren ekuazioa irudikatzeko modua.
- Irudikatzea: balio taula.
- Grafikotik ekuaziora.
- Grafikotik ekuaziora II.
Ikus, gainera
- Malda
- Osziloskopio
- Neurgailu
- Marrazketarako tresnak
Kanpo estekak
| Gai honi buruzko informazio gehiago lor dezakezu Scholian |