Eremu (fisika)

Magnitude fisiko eskalarrei dagozkienak dira. Horrelakoa da, adibidez, eguraldiari buruzko albisteetan batean telebistan erakusten den tenperaturen mapa, zeinean toki bakoitzeko tenperatura (balio eskalar bat) adierazten den. Eremu eskalarra da, halaber, likido baten barneko puntuen presioa, non likidoko puntu bakoitzari presio jakin bat (magnitude eskalarra) dagokion.

Magnitude fisiko bektorialei dagozkienak dira. Esate baterako fluido bat espazioan higitzen ari denean, puntu bakoitzaren abiadura (magnitude bektoriala) kontuan hartuz, abiaduren eremua dugu. Edo Lurraren inguruko grabitate-indarra aztertzean, puntu bakoitzeko indarra (magnitude bektoriala) kontuan hartuz, indar-eremu bektoriala izango dugu aztergai.

Kasu honetan, espazio-denborako puntu bakoitzean aztertzen ari garen magnitudea tentsore bat izango da. Adibidez, horrela gertatzen da erlatibitate orokorraren teorian Ricci-ren tentsorea aztertzean.

Eremu eskalarretan, magnitude fisikoak balio berbera duten puntuen leku geometrikoa kontsidera dezakegu, eta horrela balio bakoitzari espazioan gainazal ekipotentzial (edo isopotentzial) bat esleitu ahal diogu. Eremuaren plano batean kokatzen bagara, balio bakoitzari dagokion lerro ekipotentzial bat esleituko diogu.

Eremu bektorialetan, kontuan izan behar dugu, puntu bakoitzean magnitude fisikoak norabide geometriko bat duela. Hortaz, beste modu batera definitzen da leku geometrikoa. Puntu bakoitzean magnitudearen norabidearen ukitzailea den kurbak definitzen dira, eta  kurba bakoitzari eremu-lerroa (edo indar-lerroa) deritzo. Gauzak horrela, eremu bektorial dagoen eskualdean, bi ezaugarri hauek dituzten indar-lerroak daude: batetik, eremuko puntu bakoitza lerro bakarrean dago, eta bestetik, lerroaren bektore tangentea eta puntuko eremuari dagokion bektoreak norabide berbera dute puntu guztietan. Horrez gain, lerro horietan bektorearen noranzkoa adierazten duten geziak ere marrazten dira.

Mekanika newtondarrean, masa orok grabitazio unibertsalaren ondoriozko eremua sortzen du bere inguruko espazio osoan. Hortaz, masak dira eremu grabitatorioaren iturriak. Eremu grabitatorioa bektoriala da, zeinean indar-lerroek eremua sortzen duen masaranzko noranzkoa duten, grabitate-indarra erakarlea baita.

Lurrak eta Ilargiak osatutako sistemari dagozkion grabitatearen eremu-lerroak (kolore urdinez). Kolore gorriz lerro ekipotentzialak adierazi dira.

Masa bakarraren inguruko eremu grabitatorioko eremu-lerroek norabide erradiala dute masa-zentroan egonik.

Distantzia batera dauden bi masak osaturiko grabitate-eramuari dagozkion lerroek alboko irudiko forma dute, beti ere lerroen noranzkoa masetarako noranzkoa dutela, grabitate-indarra beti baita erakarlea.

Elkarrekintza elektromagnetikoa adierazten duen eremua da, eta izenak berak dioenez, batera doazen bi eremutan bana daiteke: eremu elektrikoa eta eremu magnetikoa, biak ala biak bektorialak izanik.

Bi karga elektrikoren inguruko eremu-lerroak. Ezkerreko irudian zeinu desberdineko bi karga; eskuinekoan, zeinu berekoak.

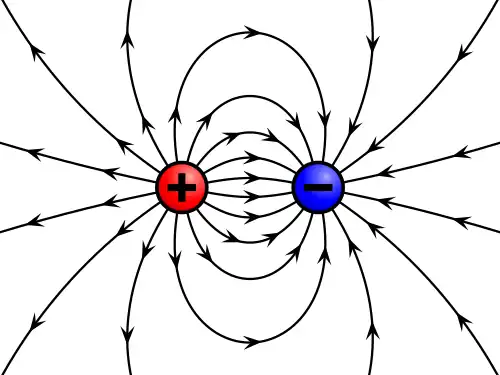
• Eremu elektrikoa. Elkarrekintza elektrostatikoa adierazten duen eremua da. Eremu elektrikoaren iturria (kausa sortzailea) karga elektrikoak dira. Horretan, kontuan izan behar da bi eratako karga elektrikoak daudela: karga positiboak eta karga negatiboak. Hori dela eta, eremu elektrikoa erakarlea zein aldarazlea izan daiteke, eremu-lerroen noranzkoa zeinuaren araberakoa baita. Karga positiboen inguruko eremu-lerroen noranzkoa kargatik kanporanzkoa da; karga negatiboen ingurukoena, kargaranzkoa. Ondorioz, bi kargak batera sorturiko eremuan, oso egitura desberdinak agertuko dira, bi kargak zeinu berekoak edo desberdinekoak izatearen arabera, alboko irukikapen grafikoan ikus daitekeenez.

Korronte elektrikoaren inguruko eremu magnetikoa.

• Eremu magnetikoa. Eremu magnetikoa korronte elektrikoek edo material magnetikoek euren inguruan sortzen duten eragina adierazten duen eremu bektoriala da. Puntu bakoitzeko eremuaren balioa bektore batez ematen da, eta ${\displaystyle {\boldsymbol {B}}}$ edo ${\displaystyle {\boldsymbol {H}}}$ sinboloaz adierazten dena. Eremu elektrikoaren lerroak ez bezala, eremu magnetikoaren lerroak itxiak dira, ez hasierarik ez amaierarik gabeak, ez baitago karga magnetiko isolaturik. Hots, ez dago monopolo magnetikorik; soilik dipolo magnetikoak.

Korronte elektrikoaren kasuan, eremu magnetikoaren lerroak korrontearen norabidearen plano perpendikular batean daude, eta zirkunferentziak dira. Imanen kasuan beti kontsideratu behar ditugu bi polo ipar poloa, ${\displaystyle {\text{N}}}$ sinboloaz adierazia, eta hego poloa, ${\displaystyle {\text{S}}}$ sinboloaz. Zeinu bereko poloek elkar aldaratzen dute eta aurkako zeinuko poloek elkar erakartzen dute. Imanen kasuko eremu-lerroak ere itxiak dira eta ibilbidea materialaren barnetik osatzen dute

Zeinu bereko poloek elkar aldaratzen dute

Aurkako zeinuko poloek elkar erakartzen dute.

Gradiente izeneko eragile bektorialak esan nahi du ${\displaystyle V}$ eremu eskalarreko puntu guztietan eragiketa hauek egin behar direla:

$${\displaystyle {\textbf {grad}}\equiv {\boldsymbol {u}}_{x}{\frac {\partial }{\partial x}}+{\boldsymbol {u}}_{y}{\frac {\partial }{\partial y}}+{\boldsymbol {u}}_{z}{\frac {\partial }{\partial z}},}$$

non ${\displaystyle {\boldsymbol {u}}_{x},{\boldsymbol {u}}_{y},{\boldsymbol {u}}_{z}}$ horiek koordenatu-sistema kartesiarreko bektore unitarioak diren. Gradiente eragilea beste sinbolo berezi batez ere adierazten da: nabla deritzo eta ${\displaystyle \nabla }$ eran adierazten da. Beraz, eragile hau baliatuz, edozein eremu eskalarretatik eremu bektorial bat erator daiteke modu honetan:

$${\displaystyle {\textbf {grad}}V\equiv \nabla V\equiv {\frac {\partial V}{\partial x}}{\boldsymbol {u}}_{x}+{\frac {\partial V}{\partial y}}{\boldsymbol {u}}_{y}+{\frac {\partial V}{\partial z}}{\boldsymbol {u}}_{z}.}$$

Horrela, ${\displaystyle V}$ eremu eskalarretik ${\displaystyle \nabla V}$ eremu bektoriala definitu da, zeinari gradiente eremua deritzon.

Dibergentzia izeneko eragile bektorialak esan nahi du eragiketa hauek egin behar direla ${\displaystyle {\boldsymbol {F}}}$ eremu bektorial bateko puntu bakoitzean:

$${\displaystyle {\text{div}}{\boldsymbol {F}}={\frac {\partial F_{x}}{\partial x}}+{\frac {\partial F_{y}}{\partial y}}+{\frac {\partial F_{z}}{\partial z}}.}$$

Hortaz, ${\displaystyle {\boldsymbol {F}}}$ eremu bektorialeko puntuetan eraginez, dibergentzia eragileak ${\displaystyle {\text{div}}{\boldsymbol {F}}}$ eremu bektoriala definitu du, zeinari dibergentzia eremua deritzon. Ohitura dago eremu bektorialaren dibergentzia ${\displaystyle \nabla }$ eragile diferentzial bektorialaren bidez adierazteko. Horrela eginik, eremuaren dibergentzia nabla bektorearen eta eremu-bektorearen arteko biderkadura eskalar gisa idatz daiteke:

$${\displaystyle {\text{div}}{\boldsymbol {F}}=\nabla \cdot {\boldsymbol {F}}.}$$

Errotazional izeneko eragile bektorialak ${\displaystyle ({\textbf {rot}}{\text{ sinboloa}})}$ esan nahi du eremu bektorial bateko puntuetan ${\displaystyle \nabla }$ eragilea aplikatzen zaiola ${\displaystyle {\boldsymbol {F}}}$ eremu-bektoreari, bien arteko biderketa bektoriala eginez:

$${\displaystyle {\textbf {rot}}{\boldsymbol {F}}\equiv \nabla \times {\boldsymbol {F}}.}$$

Osagai kartesiarretan idatziz, honelaxe adierazten dira sorturiko eremu berriaren osagaiak.

$${\displaystyle \nabla \times {\boldsymbol {F}}={\begin{vmatrix}{\boldsymbol {u}}_{x}&{\boldsymbol {u}}_{y}&{\boldsymbol {u}}_{z}\\{\frac {\partial }{\partial x}}&{\frac {\partial }{\partial y}}&{\frac {\partial }{\partial z}}\\F_{x}&F_{y}&F_{z}\end{vmatrix}}={\Bigl (}{\frac {\partial F_{z}}{\partial y}}-{\frac {\partial F_{y}}{\partial z}}{\Bigr )}{\boldsymbol {u}}_{x}+{\Bigl (}{\frac {\partial F_{x}}{\partial z}}-{\frac {\partial F_{z}}{\partial x}}{\Bigr )}{\boldsymbol {u}}_{y}+{\Bigl (}{\frac {\partial F_{y}}{\partial x}}-{\frac {\partial F_{x}}{\partial y}}{\Bigr )}{\boldsymbol {u}}_{z}.}$$

Beraz, eragile hau baliatuz, edozein ${\displaystyle {\boldsymbol {F}}}$eremu eskalarretatik ${\displaystyle {\textbf {rot}}{\boldsymbol {F}}}$ eremu bektorial bat erator daiteke, zeinari errotazional eremua deritzon. Testu anglosaxoietan ${\displaystyle {\textbf {rot}}}$sinboloa erabili ordez, ${\displaystyle {\textbf {curl}}}$ sinboloa erabiltzen da, alegia, ${\displaystyle {\textbf {curl}}{\boldsymbol {F}}}$ idazten da.

Eremuko puntu bakoitzean, eremuak balio bat du, intentsitatea deritzona. Eremu eskalarretan eremuaren beraren balioa adierazten du. Eremu bektorialetan, puntu bakoitzeko eremu bektorearen osagaien bidez definitzen den balio eskalar bat da, ${\displaystyle {\boldsymbol {E}}}$ eremuko bektorearen ${\displaystyle E}$ modulua hain zuzen. Esate baterako, eremu elektrikoaren kasuan honelaxe erlazionatzen dira eremu-bektorea eta eremuaren intentsitatea:

$${\displaystyle {\boldsymbol {E}}=E_{x}{\boldsymbol {u}}_{x}+E_{y}{\boldsymbol {u}}_{y}+E_{z}{\boldsymbol {u}}_{z}\rightarrow E={\sqrt {E_{x}^{2}+E_{y}^{2}+E_{z}^{2}}}.}$$

Intentsitatea zenbat eta handiagoa izan, hainbat handiagoa da eremuak bere inguruan sorrarazten duen efektua.

Eremu bektorialetan gaudela, bi punturen arteko ibilbide kurbatuetan, bi puntu horien artean eremuaren lerro-integralak ( integral kurbilineoak ere deituak) defini ditzakegu ibilbidean horretan zehar, era honetako integralak eginez:

$${\displaystyle I\equiv \int _{A}^{B}{\boldsymbol {E}}\cdot {\text{d}}{\boldsymbol {r}}.}$$

Adibidez, partikula bat indar-eremu batean badago, eta eremuaren eraginez partikula ${\displaystyle A}$ puntutik ${\displaystyle B}$ puntura pasatzeko ibilbide jakin bat egiten badu, integral horrek eremuak partikularen gainean egiten duen lana definituko du:

$${\displaystyle W=\int _{A}^{B}{\boldsymbol {F}}\cdot {\text{d}}{\boldsymbol {r}}.}$$

Fisikan, interesgarria da ibilbidea (integrazio-bidea) itxia den kasua aztertzea. Orduan lerro-integral horri eremuaren zirkulazioa deritzo. Magnitude horrek garrantzia du eremu bektorial batzuen kasuan. Hain zuzen, eremu kontserbakorrak deritzegu, ibilbide itxietan zehar eremuaren lerro-integral nulua duten eremu bektorialei, hots, ${\displaystyle \oint {\boldsymbol {E}}\cdot {\text{d}}{\boldsymbol {r}}=0}$ egiten duten eremuei. Eremu horiek garrantzi handia dute fisikan, eta froga daitekeenez, balditza hori betetzean, beti existitzen da eremu eskalar bat, ${\displaystyle V}$, zeinaren gradientea erremu bektorial kontserbakorra den:

$${\displaystyle {\boldsymbol {E}}=-\nabla V.}$$

Eremu eskalar horri eremu potentziala deritzo. Alegia, ${\displaystyle V}$ eremu eskalarra da ${\displaystyle {\boldsymbol {E}}}$ eremu bektorialaren eremu potentziala

Eremuko espazioaldeko gainazal bat kontsideraturik, honelaxe definitzen da eremuaren fluxua gainazal horretan zehar:

$${\displaystyle \iint \limits _{S}{\boldsymbol {E}}\cdot {\text{d}}{\boldsymbol {S}},}$$

hau da, ${\displaystyle {\boldsymbol {E}}}$ eremu bektorialaren eta ${\displaystyle {\text{d}}{\boldsymbol {S}}}$ gainazal-elementu diferentzialaren biderkadura eskalarraren gainazal-integral modura, integrala ${\displaystyle S}$ gainazal osora hedaturik. Beraz, gainazala nolakoa den, halakoa izango da fluxuaren balioa.  Fluidoen mekanikan, adibidez, fluxu hori erlazionaturik dago gainazala zeharkatzen duen fluidoaren jarioarekin.