Energia zinetiko

Erreferentzia-sistema inertzial batetik kontsideratzen den puntu material ―edo “partikula puntual”­― baten kasuan, partikulak une jakin batean duen energia zinetikoaren balioa da, zehazki, puntu hori pausaguneko egoeratik une horretako abiadurara iristeko partikulan eragiten aritu diren indarrek eginiko lanaren berdina. Zer esanik ez, aukeratutako erreferentzia-sistema inertziala ez bada, kontuan izan behar da, halaber, sistema horretan kontsideratu beharreko inertzia-indarren eragina ere. Bestela esanda, indarrek partikulan sorturiko azelerazioaren kausaz, handiagotu da beraren energia zinetikoa. Eta alderantziz, gorputzak lan-kantitate berbera emango du uneko abiaduratik geldi egoteraino dezeleratzean.

Mekanika klasikoan, gorputz puntual baten energia zinetikoa

$${\displaystyle E_{\text{k}}={\frac {1}{2}}m{v^{2}}}$$

formulaz kalkulatzen da, non ${\textstyle m}$ gorputzaren masa den, eta ${\textstyle v}$, abiadura. Masa ${\displaystyle {\text{kg}}}$-tan eta abiadura ${\displaystyle {\text{m s}}^{-1}}$-tan neurtuz gero, energia zinetikoa ${\displaystyle {\text{J}}}$-tan adierazita egongo da.

Mekanika erlatibistan, abiadura oso handien kasuan ―argiaren abiaduratik hurbil― pausagunean ${\textstyle m}$ masa duen eta ${\textstyle v}$ abiaduraz higitzen ari den partikularen energia zinetikoa honelaxe kalkulatzen da:

$${\displaystyle E_{\text{k}}={\frac {{\gamma }^{2}}{\gamma +1}}mv^{2},}$$

non ${\displaystyle \gamma ={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}}$ den (Lorentzen faktorea deritzo) eta ${\displaystyle c}$, argiaren abiadura.

Dena den, gorputzaren abiadura argiarena baino,askoz txikiagoa denean ―hau da, ${\displaystyle v\ll c}$ denean—, energia zinetikoa balio honetara hurbiltzen da:

$${\displaystyle E_{\text{k}}\thickapprox {\frac {1}{2}}m{v^{2}},}$$

eta horrela mekanika klasikoaren definiziora hurbiltzen da.

Energia zinetikoak zerikusia dauka mekanikaren beste beste magnitude batzuekin, hala nola, indarrarekin, lanarekin eta bestelako energia-motekin.

Energia zinetikoa eta lana

Indarraren eraginaren ondorioz masaren energia zinetikoa aldatzean, sistema horretan lana egin dela ondorioztatuko dugu. Lana magnitude eskalarra da —energia zinetikoaren dimentsio berbera du— eta positiboa zein negatiboa izan daiteke. Bestela esanda, edozein indar-eremutan, bi punturen artean indarrak partikulan eragindako lanak bere energia zinetikoaren aldaketa adierazten du:

Errusiar mendi bateko gurdiek energia zinetiko handiena lortzen dute beren ibilbidearen behealdean daudenean. Aldapan gorantz joatean, abiadura motelduz doa, energia zinetikoa energia potentzial grabitazional bihurtuz baitoa; ostera, aldapan beherantz joatean, alderantziz gertatzen da.

$${\displaystyle W=\Delta {E_{\text{k}}}.}$$

Indar-eremu kontserbakorrak eta energia mekanikoa

Eremu kontserbakorretan, energia potentziala (${\textstyle E_{\text{p}}}$) defini daiteke, eta eremuari dagokion indarrak eginiko lana honelaxe adierazten da bi puntu horien arteko energia potentzialen arteko inkrementuaren bidez:

$${\displaystyle W=-\Delta {E_{\text{p}}}.}$$

Hortaz,

$${\displaystyle W=\Delta {E_{\text{k}}}=-\Delta {E_{\text{p}}}.}$$

.

Hau da, eremu kontserbakorretan partikulak irabazten duen energia zinetikoa energia potentzialaren galeraren ondorioz dator. Aldiz, energia zinetikoa galtzeak energia potentzialaren irabazia dakar, hein berean. Bestela idatzita:

$${\displaystyle \Delta {E_{\text{k}}}+\Delta {E_{\text{p}}}=0\rightarrow {E_{\text{k}}}+{E_{\text{p}}}={\text{kte}}.}$$

Energia mekanikoa

Energia mekanikoa energia zinetikoaren eta energia potentzial grabitatorioaren batura da:

$${\displaystyle E_{\text{mek}}=E_{\text{k}}+E_{\text{p}}}$$

Energia potentzial hori gorputzak indar-eremu batean duen posizioagatik daukana da; adibidez, energia potentzial grabitatorioa lurrazaletik altuera batera egoteagatik daukana. Energia zinetikoa, ostera,  gorputzaren masarekin eta abiadurarekin dago erlazionatuta. Eremu grabitatorioa , eta kontserbakorra da. Ondorioz, bestelako indarrik ez dagoen kasu idealean, energia mekanikoa kontserbatu egiten da, objektuen energia mekanikoa kontante izango da higidura osoan zehar.

Denboran atzera joanda, oraindik XVII. mendearen lehen erdian, Descartes-ek (1596-1650) uste zuen higidura-kantitatea (edo gauza bera dena, momentu lineala, alegia ${\displaystyle mv}$ magnitudea) kontserbatu egiten zela. Mendearen bigarren erdian, ordea, Leibniz-ek (1646-1716) «indar bizia» (vis viva) kontzeptu berria erabili zuen, eta magnitude berri horri ${\displaystyle mv^{2}}$ balioa esleitu zion; hau da, geroko energia zinetikoaren balio bikoitza.

Willem Jacob's Gravesande-ek (1688-1742) erlazio hori garatzen zuen esperimentua egin zuen. Hain zuzen, 1721ean, Johann Bessler asmatzaile alemaniarrak asmatutako behin-betiko higidura iraunkorreko makina sortu ote zuen eztabaidatu zuen Gravesande-k (1688-1742). Gravesande, hasiera batean, ${\displaystyle mv}$ kantitate eskalarraren kontserbazioan (masa hori abiaduraz biderkatuta) oinarritutako betiko higiduraren bideragarritasunaren alde agertu zen, mekanika newtondarrak parte hartzen zuela uste baitzuen. Hala ere, 1722an, esperimentu batzuen emaitzak argitaratu zituen, non letoizko bolak altuera desberdinetatik buztin leuneko gainazal batera erortzean utzitako zuloen tamainak aztertzen baitziren. Abiadura jakin bateko bolak eginiko zuloa eta abiadura bikoitzarekin bolak eginiko zuloa elkarrekin konparatuz konturatu zenez, bigarrenak eginikoa lehenak eginikoa baino lau aldiz sakonagoa zen. Hortik ondorioztatu zuen ezen higitzen ari den gorputz baten "indar bizi"aren adierazpen zuzena ${\displaystyle m}$-rekiko proportzionala zela baina baita abiaduraren karratuaren proportzionala ere, hots, «${\displaystyle {\text{indar bizia}}\propto mv^{2}}$» zela. Beraz, Leibnizen ideiekin bat zetorrela, baina baina ez teorian soilik, esperimentuan oinarriturik ere baizik.

Geroagokoa da "energia zinetikoa" kontzeptuaren jatorria, 1829. urtean Gaspard-Gustave Coriolis-ek (1792-1843) argitaraturiko Du Calcul de l'Effet des Machines lanean abiatu zena. Ostera, “energia zinetiko” terminoa 1850. urte inguruan sortu zen, eta William Thomson (1824-1907) (Lord Kelvin izenez ere ezaguna dena) izan zen termino horren sortzailea.

Mekanika klasikoan, gorputz puntual baten edo biratzen ez duen solido zurrun baten energia zinetikoa ${\textstyle E_{\text{k}}={\frac {1}{2}}m{v^{2}}}$ formulaz kalkulatzen da, non ${\textstyle m}$ gorputzaren masa den eta ${\textstyle v}$, abiadura. Agerikoa denez, energia zinetikoa erreferentzia-sistema inertzialaren menpekoa da.

Koordenatu kartesiarrak ${\displaystyle (x,y,z)}$:

$${\displaystyle E_{\text{k}}={\frac {1}{2}}m({\dot {x}}^{2}+{\dot {y}}^{2}+{\dot {z}}^{2}).}$$

Adierazpen horretan, koordenatuen sinboloaren gainean jarritako puntuak koordenatuaren denborarekiko deribatua adierazten du, hots:

$${\displaystyle {\dot {x}}\equiv {\frac {{\text{d}}x}{{\text{d}}t}}.}$$

Koordenatu zilindrikoak ${\displaystyle (\rho ,\varphi ,z)}$

$${\displaystyle E_{\text{k}}={\frac {1}{2}}m({\dot {r}}^{2}+r^{2}{\dot {\varphi }}^{2}+{\dot {z}}^{2}).}$$

Koordenatu esferikoak ${\displaystyle (r,\theta ,\varphi )}$

$${\displaystyle E_{\text{k}}={\frac {1}{2}}m(r^{2}{\dot {\theta }}^{2}+r^{2}{\dot {\varphi }}^{2}\sin ^{2}\theta +{\dot {r}}^{2}).}$$

Higidura independenteak dituzten partikula puntualez osaturiko sistemen energia zinetikoa

Horrelako sistemen energia zinetikoa sistema osatzen duten partikula puntual guztien energia zinetikoen batura gisa defini daiteke:

$${\displaystyle E_{\text{k}}=\sum _{i=1}^{N}E_{{\text{k}}i}=\sum _{i=1}^{N}{\frac {1}{2}}m_{i}v_{i}^{2},}$$

non ${\displaystyle N}$ partikulen kopurua den, ${\displaystyle m_{i}}$ partikula bakoitzaren masa eta ${\displaystyle v_{i}}$ partikula bakoitzaren abiadura. Adierazpen hori orokorra da eta ez du aurrez kontsideratzen zein den sistemaren izaeran, alegia, sistemak egitura geometriko finkoa ote daukan edota deformagarria den ala ez.

Solido zurrunaren energia zinetikoa

Solido zurruneko bi punturen arteko distantzia konstantea da.

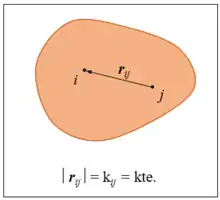
Mekanika klasikoan, solido zuzena deritzo ${\displaystyle n}$ partikulaz (kontaezinak, gehienetan) osaturiko sistema ideal bati, zeinean baldintza hau betetzen den: «edozein bi partikularen arteko distantziak konstante irauten du denboran zehar, baita solidoa higitzen ari den bitartean ere», alegia:

$${\displaystyle \mid {\boldsymbol {r}}_{i}-{\boldsymbol {r}}_{j}\mid =\mid {\boldsymbol {r}}_{ij}\mid ={\text{k}}_{ij}={\text{kte.}}}$$

Alboko irudian modu eskematikoan adierazi da solido zurrunaren definizio hori,

Bestalde, solido zurrunaren eredu idealean, partikula puntual bakoitzaren masa  mi izanik, solidoaren masa totala partikulen masa guztien batura da eta honelaxe adierazten da:

$${\displaystyle M=\sum _{i=1}^{N}m_{i}.}$$

Berdin gertatzen da gainerako magnitude estentsiboen kasuan, non solido zurrun osoari dagozkion balioak partikula guztiei dagozkien balioen batura batura eginez lortzen diren, hala nola momentu linealaren edo energia zinetikoaren kasuan:

$${\displaystyle {\boldsymbol {P}}=\sum _{i=1}^{N}m_{i}{\boldsymbol {v}}_{i},}$$

$${\displaystyle E_{\text{k}}={\frac {1}{2}}\sum _{i=1}^{N}{m_{i}}v_{i}^{2}.}$$

Zer esanik ez  beti kontuan izan behar da magnitudearen izaera, hots eskalarra ala bektoriala den.

Solido zurrunaren masa-zentroa

Solido zurruaren energia zinetikoa kalkulatzeko, egokia da solidoaren masa-zentroa deritzon kontzeptua erabiltzea. Solido zurrun bati erreferentzia-sistema batean dagokion masa-zentroa honelaxe definituriko puntua da:

$${\displaystyle {\boldsymbol {r}}_{\text{MZ}}\equiv {\frac {\sum _{i=1}^{N}m_{i}{\boldsymbol {r}}_{i}}{\sum _{i=1}^{N}m_{i}}}.}$$

Biraka ari den solido zurrunaren energia zinetikoaren kalkulurako magnitudeen eskema.

Biraka ari den solido zurrunaren energia zinetikoa

Biraka ari den solido zurrunaren kasuan, energia zinetiko osoa bi osagairen batura gisa deskonposa daiteke: translazioari dagokion energia zinetikoa ( masa-zentroa espazioan zehar abiadura berberaz higitzeari legokiokeena) eta biraketari dagokion energia zinetikoa (biraketan duen abiadura angeluarrari legokiokeena). Matematikoki idatzita, hauxe da solido zurrunari dagokion energia zinetiko osoa:

$${\displaystyle E_{\text{k}}={\frac {1}{2}}MV^{2}+{\frac {1}{2}}I\omega ^{2},}$$

non ${\displaystyle M}$ solidoaren masa osoa den, ${\displaystyle V}$ masa-zentroaren abiadura, ${\displaystyle I}$ biraketa-ardatzaren inguruko inertzia-momentua eta ${\displaystyle \omega }$ biraketako abiadura angeluarra.

Formula horretan agerikoa denez, energia zinetikoa bi osagairen batura da: lehen osagaia —${\textstyle {\frac {1}{2}}MV^{2}}$— solidoaren masa-zentroaren translazioari dagokio, eta bigarrena —${\textstyle {\frac {1}{2}}I\omega ^{2}}$—, solidoaren biraketari. Agerikoa denez, solidoa biratzen ari ez bada, hauxe izango da honakoa izango da energia zinetikoaren balioa:

$${\displaystyle E_{\text{k}}={\frac {1}{2}}MV^{2},}$$

hau da, translazioari dagokiona; edo bestela esanda, solidoaren masa guztia masa-zentroan kontzentraturik balego edukiko lukeena.

Energia termikoa energia-mota bat da, materia osatzen duten molekula eta atomoen energia zinetikoari dagokiona.

Beroaren, tenperaturaren eta atomoen eta molekulen energia zinetikoaren arteko erlazioa mekanika estatistikoaren eta termodinamikaren helburua da.

Mekanika erlatibistan, aldatu egin behar energia zinetiko klasikoaren adierazpena abiadura oso handien kasuan, alegia, argiaren abiadurara hurbiltzen ari diren partikulen kasuan. Zehazki, honelaxe adierazi behar da  energia zinetiko erlatibista:

$${\displaystyle E_{\text{k}}=m\gamma {c^{2}}-mc^{2}={\frac {mc^{2}}{\sqrt {1-v^{2}/c^{2}}}}-mc^{2}.}$$

Adierazpen horretan, ${\textstyle m}$ masa, ${\textstyle v}$ partikularen abiadura, ${\textstyle c}$ argiaren abiadura eta ${\textstyle \gamma }$ faktorea —Lorentzen faktorea edo gamma faktorea ere baderitzo— ageri dira. Energiaren adierazpen erlatibistak erakusten duenez, partikularen abiadura argiaren abiadurara hurbildu ahala, ${\textstyle \gamma ={\frac {1}{\sqrt {1-v^{2}/c^{2}}}}}$ gero eta handiagoa egiten da eta energia zinetikoak infiniturako joera hartzen du. Beraz, argiaren abiadura muga bat da, masadun partikulek lortu ezin dutena.

Beste ondorio bat ere atera daiteke formula horretatik, zeren ${\textstyle mc^{2}}$ terminoak partikularen pausaguneko energia adierazten baitu, eta horixe da hain zuzen, Einsteinek azaldutako masaren eta energiaren baliokidetza adierazten duen formula ospetsua: ${\textstyle E=mc^{2}}$.

• energia
• energia potentziala
• energia mekanikoa
• masa inertziala

• Fishbane, Paul (2008) Fisika zientzialari eta ingeniarientzat. 1. bolumena, (1.etik-21.era Gaiak) Universidad del País Vasco/Euskal Herriko Unibertsitatea ISBN 9788490820308 PMC932800438.
• Etxebarria Bilbao, Jose Ramon (arg.) Fisika orokorra (2. argitalpena) UEU, Bilbo (2003) ISBN 9788484380450.
• J.R. Etxebarria & F. Plazaola, Mekanika eta Uhinak, UEU, Bilbo (1992) ISBN 84-86967-42-2

• Marcelo Alonso, Edward J. Finn (1976). Física. Fondo Educativo Interamericano. ISBN: 8403209908; 8403202334; 8403209908; 9686 BC37.