Determinante

Determinante batek ekuazio sistema linealen soluzioen bakartasuna biltzen du. Cardanok 2 ordenako kasu baterako erabili zuen 1545ean, Ars Magna obrarako, bi ezezagun eta bi ekuazio dituen sistema bate soluzioa bilatzeko lege bezala.

Ordena handiagoko determinanteak 100 urte baino beranduago heldu ziren. Seki Takakazu japoniarraren eta Leibniz alemaniarraren eskutik heldu ziren horiek.

Leibnizek ekuazio sistema lineal ezberdinak aztertu zituen. Idazkera matriziala falta zenez, ezezagunen koefizienteak indize pareekin errepresentatzen zituen, horregatik ij erabiltzen zuen a_ij adierazteko. 1678an 3 ezezagun eta 3 ekuaziotako sistemetan interesatu zen, eta ordena hortako formularen zutabe baten gainean egindako garapena lortu zuen. Urte berean 4 ordenako determinante bat idatzi zuen eta zeinua izan zen egindako akats bakarra. Lan hori ez zen argitaratua izan eta emaitzak 50 urte beranduago aurkitu zituzten, era independientean.

Denbora tarte berean Kowa Sekik determinanteei buruzko eskuizkribu bat argitaratu zuen. Bertan, interpretatzen zailak diren formula orokorrak ageri dira. Formula horiek zuzenak dira 3 eta 4 ordenako matrizeentzat, ordena handiagoko matrizeetan zeinuak txarto adierazten dira.

1748an, MacLaurinen aljebraren tratatu batean n ezezaguneko n ekuazio linealek osatzen duten sistemaren soluzioa aurkitzeko legea azaltzen da, n 2,3 edo 4 delarik. Soluzio hori determinanteen erabileraren bidez ematen da. 1750ean, Cramerrek edozein ordenako sistemaren soluzioaren legea adierazi zuen, baina ez zuen frogapenik adierazi.

Bezoutek 1764an argitaratutako artikuluaren ondorioz hainbat matematikari determianteen gaiarekin interesatu ziren. 1772an Laplacek Laplaceren legeak ezarri zituen. Urte bat beranduago, Lagrangek determinanteen eta bolumenen kalkuluen arteko erlazioaz jabetu zen.

Gaussek determinante hitza Disquisitiones arithmeticae liburuan (1801) erabili zuen lehenengoz. Gaur egun koadrika baten desberdintze bezala ezagutzen dugunaren sinonimotzat erabili zuen, eta determinante modernoaren kasu partikular bat da. Hala ere produktu baten determinantearen teorema lortzetik hurbil izan zen.

Cauchy izan zen determinantearen esanahi modernoa erabiltzen lehena. Aurretik zeuden ezagutzen laburpena egiteaz arduratu zen eta 1812an produktu baten determinantearen formula eta bere frogapena argitaratu zituen, Laplacen legearen enuntziatu eta frogapenarekin batera. Urte berean, Binetek produktu baten determinantea lortzeko beste formula bat (okerra) argitaratu zuen. Garai hartan, Cauchyk endomorfismoaren erredukzioaren inbestigaziorako oinarriak ezarri zituen.

1825ean Heinrich F. Scherkek determinantearen propietate berri batzuk argitaratu zituen. Horietako bat hurrengoa zen: Matrize bateko ilara bat beste ilara baten konbinazio lineala bada, matrize horren heina 0 izango da.

Jacobik famatu egin zuen determinanteen auzia, 1841ean Crelle aldizkarian determinanteei buruzko hiru tratatu argitaratu zituenean. Modu algoritmiko batean oinarritutako kalkulatzeko metodo sistematikoak aurkeztu zituen lehenengo aldiz. Modu berean, funtzioen determinanteen ebaluazioa posible egin zuen definizio jacobiarrari esker, eta horrek determinante kontzeptuaren abstrakzioan garapen handiak ekarri zituen.

Kuadro matriziala Cayley y James Joseph Sylvesterek ezarri zuten. Cayley bera izan zen matrizeen barra bertikalezko notazioaren sortzailea (1841) eta matrizeen alderantzizkoa lortzeko matrizeen bidezko formula ezarri zuen (1858).

Determinanteen teoria simetria partikularren propietateak dituzten determinanteei eta determinanteak matematikako beste arlo batzuetan erabiltzen hasi izateari esker indarberritu zen.

Beheko mailako matrizeen kasua (1., 2. edo 3. ordena) oso sinplea da, eta determinantea arau ezagun sinpleen bidez kalkulatzen da. Arau horiek Laplaceren teorematik ere ondoriozta daitezke.

Bat ordenako matrize bat, kasu tribiala da, baina kasu guztiak osatzeko tratatuko dugu. Bat ordenako matrize bat eskalar bat bezala trata daiteke, baina hemen bat ordenako matrize karratu bat kontsideratuko dugu:

${\displaystyle \mathrm {A} ={\begin{bmatrix}a_{11}\end{bmatrix}}}$

Determinantearen balioa matrizearen termino bakarraren berdina da:

${\displaystyle det\mathrm {A} =det{\begin{bmatrix}a_{11}\end{bmatrix}}=a_{11}}$

Bi ordenako matrize baten determinanteak:

${\displaystyle \mathrm {A={\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix}}} }$

formula honen bidez kalkulatzen dira:

${\displaystyle |\mathrm {A} |={\begin{vmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{vmatrix}}=a_{11}a_{22}-a_{12}a_{21}}$

Hiru ordenako matrizea izanik:

${\displaystyle \mathrm {A} ={\begin{bmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{bmatrix}}}$

Hiru ordenako matrize baten determinantea Sarrusen erregelaren bidez kalkulatzen da:

${\displaystyle |A|={\begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{vmatrix}}=(a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32})-(a_{31}a_{22}a_{13}+a_{32}a_{23}a_{11}+a_{33}a_{21}a_{12})}$

n ordenako determinatzailea Laplaceren teoremaren bidez kalkula daiteke ilara edo zutabe batetik abiatuta eta problema n-1 ordenako n determinatzaileen kalkulura murriztuz. Horretarako, edozein ilara edo zutabe hartzen da elementu bakoitza bere kofaktorearengatik biderkatuz. ${\displaystyle a_{ij}:}$ matrizearen elementu kofaktorea da, eta elementu horri dagokion errenkada eta zutabea ezabatzean eta (-1)^i+j, eta (-1) i+j-rekin biderkatuz, non i errenkada-zenbakia eta j zutabe-zenbakia diren, lortzen da matrizearen determinatzailea. Ilara (edo zutabe) bateko elementuen produktu guztien batura haien kofaktoreengatik biderkatuta, determinatzailearen berdina da.

4. ordenako determinatzaile baten kasuan, zuzenean, 3. ordenako determinatzaileak lortzen dira, eta horiek Sarrusen arauaren arabera kalkulatu ahal izango dira. Aldiz, goiko ordenako determinatzaileetan, n=5 kasu, 4. ordenako determinatzaileak lortuko ditugu lerro baten elementuak garatzean, eta horiek, aldi berean, metodo berean garatu beharko dira 3. ordenako determinatzaileak lortzeko. Adibidez, zehaztutako metodoarekin 4. ordenako determinatzaile bat lortzeko, 3. ordenako 4 determinatzaile kalkulatu behar dira. Hori arindu daiteke baldin eta aurretik errenkada edo zutabe batean hiru zero lortzen badira, eta, orduan, nahikoa izango da 3. ordenako determinatzaile bat kalkulatzea (izan ere, gainerako determinatzaileak 0z biderkatuta egongo dira, eta horrek baliogabetu egiten ditu).

Eragiketa kopurua oso azkar handitzen da. Adibidez, metodo horren bidez, 10 ordenako determinatzaile baterako, 3. ordenako 10 x 9 x 8 x 7 x 6 x 5 x 4 = 604.800 determinatzaile kalkulatu beharko dira.

Gaussiana ezabatzeko metodoa ere erabil daiteke matrizea matrize triangeluarra bihurtzeko.

Determinatzaileen kostu konputazionala murrizteko eta biribiltze-akatsen aurrean egonkortasuna hobetzeko, Chioren araua aplikatzen da. Horri esker, matrizearen triangularizazio-metodoak erabil daitezke, eta, horrela, determinatzailearen kalkulua matrizearen diagonaleko elementuen biderkadurara murrizten da. Triangularizaziorako, zenbakiz egonkorra den edozein metodo erabil daiteke. Horiek matrize ortonormalen erabileran oinarritzen dira, Gaussen metodoa, Householderren gogoetak edo Givensen errotazioak erabiltzean gertatzen den bezala.

Zenbait baldintzapean, dimentsio infinituko Banachen espazio bektorial baten aplikazio linealen determinatzailea defini daiteke. Zehazki, determinatzailean, definituta dago determinatzaile klaseko operadorerentzat, traza klaseko operadoreak oinarri hartuta. Adibide nabarmen bat Fredholmen determinatzailea izan zen; honek bere izena daraman ekuazio integrala azterketarekin lotuta definitu zuen:

${\displaystyle f(x)=\phi (x)+\int _{0}^{1}K(x,y)\phi (y)\ dy}$

non

${\displaystyle f(x)\,}$ ezagututako funtzioa den

${\displaystyle \phi (x)\,}$ funtzio ezezaguna den

${\displaystyle K(x,y)\,}$ nukleo izeneko funtzio ezaguna den eta, Hilbert-en espazioan, karratu integragarriaren funtzioa (0,1) bitarteko hurrengo operadore lineal trinko eta finitua sortzen duen.

${\displaystyle {\hat {K}}:L^{2}[0,1]\to L^{2}[0,1],\quad ({\hat {K}}\phi )(x)=\int _{0}^{1}K(x,y)\phi (y)\ dy}$

(*) ekuazioak soluzioa du Fredholm-en ${\displaystyle \det(I+{\hat {K}})}$ determinatzailea baliogabetzen ez bada. Fredholmen determinatzaileak, kasu honetan, determinatzailea dimentsio finituan orokortzen du, eta esplizituki kalkula daiteke honako hauen bidez:

${\displaystyle \det(I+{\hat {K}})=\sum _{k=0}^{\infty }{\frac {1}{k!}}\int _{0}^{1}\dots \int _{0}^{1}\det[K(x_{i},x_{j})]_{1\leq i,j\leq k}\ dx_{1}\dots dx_{k}}$

(*) ekuazioaren soluzio bera modu sinplean idatz daiteke determinatzailearen terminoetan, determinatzaile hori baliogabetzen ez denean.

1. irud. Determinatzailea orientatutako eremu urdina da.

Bada P plano euklideoa. X eta X' bektoreen determinatzailea adierazpen analitikoarekin lortzen da

${\displaystyle \det(X,X')={\begin{vmatrix}x&x'\\y&y'\end{vmatrix}}=xy'-yx'}$,

edo, modu baliokidean, adierazpen geometrikoaren arabera

${\displaystyle \det(X,X')=\|X\|\cdot \|X'\|\cdot \sin \theta }$,

non ${\displaystyle \theta }$ X eta X' bektoreek osatzen duten angelua orientatua den.

• Determinatzailearen balio absolutua paralelogramoaren azaleraren berdina da, eta X eta X'z definitzen da (${\displaystyle X'\sin \theta }$, eta paralelogramoaren altuera da, beraz, A = Oinarria × Altuera).
• Determinatzailea nulua da, baldin eta bi bektoreak kolinealak badira (paralelogramoa lerro bihurtzen da).
• * Haren zeinua erabat positiboa da baldin eta '(X, X') angeluaren neurria ]0, ${\displaystyle \pi }$[-(e)n badago.
• Determinatzailearen aplikazioa bilineala da: lehen bektorearekiko linealtasuna

${\displaystyle \det(aX+bY,X')=a\det(X,X')+b\det(Y,X')\;}$ idazten da,

eta bigarrenari dagokionez:

${\displaystyle \det(X,aX'+bY')=a\det(X,X')+b\det(X,Y')\;}$.

2. Irud. Alboko bi paralelogramoko eremuen batura.

2. irudiak, planoan, formula horren kasu berezi bat ilustratzen du. Alboko bi paralelogramo irudikatzen ditu; batak u eta v bektoreek definitzen dute (berdez), eta besteak u' eta v bektoreek (urdinez). Adibide horren gainean, u+u' eta v (grisez) bektoreek definitutako paralelogramoaren azalera ikustea erraza da: triangelu baten azalera kendu, eta beste triangelu baten azalera gehitzen zaion aurreko bi paralelogramoen baturaren berdina da. Bi triangeluak translazioaren araberakoak dira, eta hurrengo formula egiaztatzen da: Det (u+u', v)=Det (u, v)+Det (u', v).

Irudia aldebikotasun-formularen kasu berezi bati dagokio, orientabideak eremuek zeinu bera izateko moduan aukeratu baitira eta eduki geometrikoa ulertzen laguntzen.

B oinarri ortonormal zuzena duen plano euklidear batean defini daiteke determinatzailearen nozioa oinarri horretako bektoreen koordenatuak erabiliz. Determinatzailearen kalkuluak emaitza bera ematen du kalkulurako aukeratutako zuzeneko oinarri ortonormala edozein dela ere.

E 3 dimentsioko espazio euklideoa bada, E-ren hiru bektoreren determinatzailea honela ematen da:

${\displaystyle \det(X,X',X'')={\begin{vmatrix}x&x'&x''\\y&y'&y''\\z&z'&z''\end{vmatrix}}=x{\begin{vmatrix}y'&y''\\z'&z''\end{vmatrix}}-x'{\begin{vmatrix}y&y''\\z&z''\end{vmatrix}}+x''{\begin{vmatrix}y&y'\\z&z'\end{vmatrix}}=xy'z''+x'y''z+x''yz'-xy''z'-x'yz''-x''y'z.}$

3. irud. Trilinealitatearen ilustrazio grafikoa.

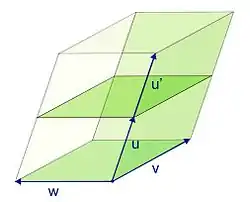
Determinatzaile horrek produktu misto izena hartzen du.

• Determinatzailearen balio absolutua hiru bektoreek definitutako paralelepipedo-bolumenaren berdina da.
• Determinatzailea nulua da, baldin eta hiru bektoreak plano berean badaude (paralelepipedo laua).
• Aplikazio erabakigarria trilineala da: batez ere

${\displaystyle \det(aX+bY,X',X'')=a\det(X,X',X'')+b\det(Y,X',X'')\,}$

Ezaugarri horren ilustrazio geometrikoa 3. irudian dago, alboko bi paralelepipedorekin, hau da, aurpegi komun batekin. Hurrengo berdintasuna begiesgarria da:

${\displaystyle \det(u+u',v,w)=\det(u,v,w)+\det(u',v,w)\,}$.