Denboraren zabalkuntza

Erlatibitate bereziaren bigarren postulatuaren arabera edozein erreferentzia sistematan argiaren hutseango abiadura konstantea da. Hau da, argiaren abiadura ez da behatzailearen eta iturriaren mendekoa eta bere balioa ${\displaystyle c}$ da. [10][11][12][13]Demagun bi ispilu bertikalez osatutako erlojua dugula. A puntua ukitzen duen bakoitzean erlojuaren tik bat izango da.

Erlojua geldirik dagoen erreferentzia sistema batean erraz kalkula dezakegu erlojuaren periodoa:

${\displaystyle \Delta t=2L/c}$

${\displaystyle v}$ abiaduraz higitzen ari den behatzaile baten erreferentzia sistema inertzialean ez da hain tribiala kalkulatzea. Hala ere, argiaren abiadura konstantea denez sistema inertzial guztietan trigonometria erabiliz ere arin lor dezakegu:

• 
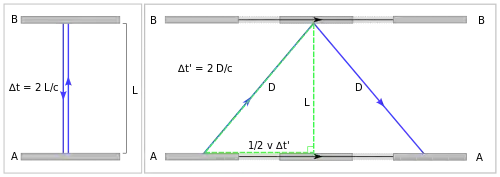  Ezkerraldean erlojua geldirik dagoen erreferentzia sistematik periodo bat irudikatuta. Eskuinaldean, v abiaduraz mugitzen den behatzaile baten erreferentziatik periodoa ere irudikatuta

Erreferentzia sistema higikorrean periodoa ${\displaystyle \Delta t'=2D/c}$ izango da non ${\displaystyle D}$ trigonometria erabiliz ezagut daiteke

${\displaystyle D={\sqrt {\left({\frac {1}{2}}v\Delta t'\right)^{2}+L^{2}}}}$

${\displaystyle L}$ aurreko erreferentziaren ekuaziotik askatuz, ${\displaystyle L=\Delta t\cdot c/2}$ eta ordezkatuz, bi erreferentzia sistemen denbora tarteen arteko erlazioa

${\displaystyle \Delta t'={\frac {\Delta t}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}}$

${\displaystyle \gamma ={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}}$ dela kontuan hartuz berridatz daiteke modu laburrago batean:

${\displaystyle \Delta t'=\gamma {\Delta t}}$

${\displaystyle v<c}$ denez, ${\displaystyle \gamma \geq 1}$ izango da, hau da, erlojuarekiko higitzen ari den behatzailearen denbora tartea erlojua gelditzat duen behatzailea baino handiagoa da. Halaber, geldiuneko sisteman erloju guztiek periodo berdina badute, denek zabalkuntza berdina jasan behar dute, erloju motaren gorabehera (mekanikoa, elektrikoa, optikoa...)[14]

Demagun argi iturri bat dugula haga bertikal batean kokatuta. Haga hari laborategiko ikuspuntutik ikusita ${\displaystyle v}$ abiaduraz higitzen da eskuinerantz. Argi iturritik fotoi bat ateratzen da eta hagaren ikuspuntutik ${\displaystyle t'}$ segundu behar ditu Lurra jotzeko, beraz egindako distantzia ${\displaystyle ct'}$ izango da. Laborategiko ikuspuntutik ${\displaystyle t}$ denbora behar izan du eta tarte horretan haga ${\displaystyle vt}$ distantzia desplazatu da eskuinera. Kontuan izan behar dugu higidura erlatiboa norabide horizontalean gertatzen ari dela eta ez bertikalean, beraz bertikalki kokatuta dagoen hagaren zatiak ez du uzkurdurarik edo efekturik jasango. Bientzat fotoiak egindako distantzia bertikala berdina da. Honek dakar, distantzia horren karratua hartzean:

${\displaystyle c^{2}t'^{2}=c^{2}t^{2}-v^{2}t^{2}}$

Edo berridatziz,

${\displaystyle t'=t(1-v^{2}/c^{2})^{1/2}}$

Hemen berriro ere, denboraren zabalkuntza ageri da.

Bi behatzaile baditugu eta haien arteko abiadura erlatiboa ez nulua bada, orduan bakoitzaren erreferentzia sisteman kokatuta bestea higitzen dagoela esango genuke eta hortaz, bere erlojua motelago doala. Logikak esango liguke, erlojua motelago doan erreferentzia sistema horretako behatzaile batek kanpoko munduaren denbora azkarrago doala hautemango lukeela, erlatibitate bereziak, haatik, intuizioaren aurkakoa aurresaten du: erreferentzia sistema bakoitzak bestearen erlojua motelago doala ikusiko du. Honek paradoxa bat ematen du, baina Lorentzen transformazioei erreparatzen badiegu ikusiko dugu xehetasun gehiago daudela.

Demagun bi erreferentzia sistema ditugula, ${\displaystyle S}$ eta ${\displaystyle S'}$, bakoitza erloju propio batekin eta ${\displaystyle S'}$ ${\displaystyle v}$ abiaduraz aldentzen ${\displaystyle X}$ ardatzean zehar (kontsideratuko dugu dimentsio bakarreko higidura). ${\displaystyle S}$-rentzat ${\displaystyle S'}$-ren posizioa ${\displaystyle x=-vt}$ da eta bere posizioa ${\displaystyle x=0}$ (konstantea)

Denborarako Lorentzen transformazioa

${\displaystyle t'=\gamma (t-{\frac {vx}{c^{2}}})}$

${\displaystyle x=0}$ ${\displaystyle denean}$ ${\displaystyle t'=\gamma t}$

${\displaystyle x=-vt}$ ${\displaystyle denean}$ ${\displaystyle t'=\gamma (t+{\frac {v^{2}t}{c^{2}}})={\frac {1}{\gamma }}t}$.

Horrek adierazten digu, posizioaren menpekotasuna dagoela. ${\displaystyle x=0}$ posizioan, ${\displaystyle S'}$-ak denbora tarte luzeagoa ikusten du ${\displaystyle S}$-k baino eta ${\displaystyle x=-vt}$ posizioan ${\displaystyle S'}$ denbora tarte laburragoa igaro dela ikusten du.

Elkarrekikotasunaren fenomenoa bikien paradoxara eramaten gaitu, non bikietako batek Lurrean gelditzen den eta eta bestea espazio-bidaia batean ontziratzen den, elkarrekikotasuna iradokitzen du biki bakoitzaren ikuspuntutik besteak zaharragoa izango dela, baina biak berriro elkartzean, bien erreferentzia sistema berbera izango da eta hortaz, adin berdina eduki beharko dute. Hori ez da benetan kasua, paradoxa biki bidaiariaren azelerazioarekin konpon daiteke; bidaztiak nonbaiten buelta eman behar duenez, azeleratu behar izan du nahitaez.[17][18] Azelerazio horrek eragin du denboraren zabalkuntza asimetrikoa eta honen ondorioz, elkartzean Lurrera bueltatuko bikia zaharragoa izango da. Hala ere, hori ez da eman daitekeen azalpen bakarra, gainera azeleraziorik gabe ere bidaiariak gazteagoa izango dela ondorioztatzen da.

Uhin batekiko higidura erlatiboa duen behatzaile batek ikusten duen uhinaren maiztasun aldaketari Doppler efektua deritzo. Ives eta Stilwell (1938) esperimentu batzuk gauzatu zituzten Doppler efektua erabiliz denboraren zabalkuntza frogatzeko. Esperimentu horietan izpi katodikoen bidez, izpiak aurrez aurretik edo atzealdetik zetozenean aztertu zituzten.

Demagun ${\displaystyle v}$ abiaduraz mugitzen den izpi-iturria dugula.

Denboraren zabalkuntza kontuan hartu gabe, Doppler formula honelakoa da:

${\displaystyle f'=f(1-{\frac {v}{c}}\cos {\theta })}$

Denboraren zabalkuntza kontuan hartuz, Doppler formula honelakoa da:

v abiaduraz mugitzen den izpi iturriak uhina f maiztasunarekin igortzen du

${\displaystyle f'=f\gamma (1-{\frac {v}{c}}\cos {\theta )}}$

non ${\displaystyle f'}$ behatzaileak detektaturiko maiztasuna den eta ${\displaystyle f}$ iturriak igorritakoa. Esperimentua ${\displaystyle \theta =0,\pi }$ balioetan egin zen:

Uhina behatzailera hurbiltzen ari bada ${\displaystyle f'}$ neurtuko du:

Denboraren zabalkuntza gabe

${\displaystyle f'=f(1-{\frac {v}{c}})}$

Denboraren zabalkuntzarekin

${\displaystyle f'=f\gamma (1-{\frac {v}{c}})}$

Uhina behatzailetik aldentzen ari bada ${\displaystyle f''}$ neurtuko du:

Denboraren zabalkuntza gabe

${\displaystyle f'=f(1+{\frac {v}{c}})}$

Denboraren zabalkuntzarekin

${\displaystyle f'=f\gamma (1+{\frac {v}{c}})}$

Denboraren zabalkuntza gabe, ${\displaystyle f}$ beste bi maiztasunen erdian egongo litzateke baina hori ez da neurtu zena, neurtutako balioak ez ziren klasikoki esperotakoak, ${\displaystyle \gamma }$ faktorea duten adierazpenak lortu zituzten.

Hasselkamp, Mondry eta Scharmanek[19] angelu zuzenetarako neurtu zuten efektua 1979an. Einsteinek ondorioztatu zuen moduan ${\displaystyle \theta =\pi /2}$ denean ${\displaystyle f'=f\gamma }$ betetzen da. Geldiunean dagoen erreferentziaren maiztasun txikitze hori denboraren zabalkuntzaren ondorioa da eta zeharkako Doppler efektutzat ezagutzen da.

Muoiak leptoi familiako oinarrizko partikulak dira. Oso masiboak dira (207 aldiz elektroiaren masa). Lurreko goi atmosferan eratzen dira oso energia altuko protoien talken ondorioz. Sortuak diren altuera 10 kilometroko magnitude ordenakoa izan ohi da. Muoiak ezegonkorrak dira eta ${\displaystyle 2\cdot 10^{-6}s}$ behar dituzte neutrino eta elektroi batean desintegratzeko. Lurreko gainazalera minuturo 10.000 muoi ailegatzen dira metro karratu bakar batean, baina nahiz eta abiadura erlatibista dutela onartu (${\displaystyle 0.9999c}$), fisika klasikoak 600 metro baino distantzia laburragoa egin dezaketela adierazten digu. Klasikoki ezinezkoa da guk Lurrean muoien presentzia nabaritzea, halarik ere, neurtzen ditugu.[20] Erlatibitate bereziak azalpen egokia eman dezake: Lurretik ikusita, denboraren zabalkuntzak bere bizi iraupena luzatzen du ${\displaystyle \Delta t'=\gamma \Delta t=1,4\cdot 10^{-4}s}$ . Guk genekien ${\displaystyle 2\cdot 10^{-6}s}$ behar zituela geldiuneko erreferentzia sisteman, hau da, muoiaren ikuspuntutik hori da behar duena, baina Lurreko behatzaile batek ez du hori ikusiko, denbora luzeagoan desintegratzen dela neurtuko du. Denbora tarte horretan ${\displaystyle 42km}$ egin ditzake, distantzia nahikoa gainazala ukitzeko. Hori horrela, zein da muoiaren ikuspuntutik gertatzen dena? Bere erreferentzia sisteman bera da geldirik dagoena eta Lurra argiaren ${\displaystyle \%99,99}$ abiaduraz hurbiltzen zaiona. Kasu honetan, muoiak atmosferaren kontrakzioa nabaritzen du (Lorentzen uzkurdura deitzen zaio fenomeno honi). Labur esanda, muoiarentzat atmosfera oso fina bilakatzen da (${\displaystyle 2\cdot 10^{-6}s}$-tan zeharkatzeko modukoa) eta berehala zeharkatzen du. Bi ikuspegiak zuzenak dira eta nahiz eta bi interpretazio oso desberdin izan, azkenean bietan muoiak gainazala ukitzen du.[21][22]

Partikula azeleragailuetan sortutako partikulen bizi iraupena ere luzeagoa da denboraren zabalkuntza dela eta. Muoiaren desintegrazioa eragiten duten prozesuak muoiaren ikuspuntutik laborategian ikusten den erritmo desberdinean gertatzen dira. Ohizko fenomenoa da eta zehaztasunez aztertuta izan da. Adibidez, CERN-eko muoi biltegirako eraztunean muoien (${\displaystyle \gamma =29,327}$) bizi iraupena ${\displaystyle 64,378\mu s}$-ko zabalkuntza zuela neurtu zen.[23]

C erlojua A eta B erloju sinkronizatuekiko abiadura erlatiboan.

Denboraren zabalkuntza grafikoki adierazteko Minkowskiren diagramak erabiliko ditugu. Demagun hiru erloju ditugula, A, B eta C. C S' erreferentzia sisteman geldiunean dago, A eta B S-n geldiunean daude. C-k A-rekin topo egiten du d-n eta B-rekin f-n. 3 Erlojuak aldi berean martxan jartzen dira ( tik egiten) S-n. Bakoitzaren mundu lerroak: A-rena ct, B-rena ct-rekiko paraleloa baina f ebakitzen duena eta C-rena ct'. d-rekiko aldi berekoak diren gertaerak S-n X ardatzean daude, S'-n, aldiz, X' ardatzean.

Bi gertakarien arteko denbora propioa bietan presente dagoen erlojuak adierazten du.[24] Aldaezina da; sistema inertzial guztiek ados daude denbora propioaren balioarekin. Gure adibidera bueltatuz, df da C erlojuaren denbora propioa eta ef=dg (S-n) baino laburragoa da. Modu berean, B-ren ef denbora propioa laburragoa da if denborarekiko S'-n.

Hiperbola inbarianteak

Hortik ondoriozta daiteke, bi gertakarien arteko denbora propioa beti da bi gertakizun horien arteko denbora minimoa, hau da, beste edozein erreferentzia sistema inertzialetan denbora luzeagoa neurtuko da.

Beste era bat denboraren zabalkuntza irudiztatzeko hiperbola aldaezinen erabilpenean datza. Horretarako ${\displaystyle \Delta s^{2}}$inbariantea erabiltzen da. Dimentsio bakarrean egingo dugu kalkulua erraztasunagatik, beraz,

${\displaystyle \Delta s^{2}=c^{2}t^{2}-x^{2}=c^{2}t'^{2}-x'^{2}}$

Kalibratzeko hauxe erabiliko dugu:

${\displaystyle \Delta s^{2}=c^{2}t^{2}-x^{2}=c^{2}t'^{2}-x'^{2}=\pm 1}$

Hiperbola hauen proiekzioak eginez ere erraz konproba daiteke denboraren zabalkuntza.

Ondorengo adibidearen bitartez ikusiko da zergatik garrantzia duen denbora propioak. Demagun c abiaduratik gertu higitzen doan gidari batek Bilbotik Gasteizerako bidean doala. Bidean zehar hainbat erloju ikusiko ditu errepidean eta badaki garaiz iritsi behar dela hirira. Hiriaren erlojua errepidekoa izango da, geldirik dagoena, eta aldiz, gidariaren erloju propioak bere metabolismoa edota bihotz taupaden erritmoa markatuko du. Beraz, garaiz iritsiko den konprobatzeko errepideko ordulariei erreparatu beharko die eta bazkaltzeko ordua den edo ez jakiteko denbora propioari. Kontuan izan, errepidekoa ${\displaystyle dt}$ tartea igaro dela esatean propioak tarte laburragoa adieraziko du, ${\displaystyle d\tau }$

${\displaystyle d\tau =dt/\gamma }$

Ohiko abiaduretan ${\displaystyle \gamma }$ baten inguruan egongo da, hortaz ez dugu ezer hautematen baina partikulen fisikan desberdintasuna oso garrantzitsua da.

Inferentzietan egiten dena gehiago orokortu daiteke Lorentzen transformazioak erabilita.[25] Demagun bi gertakizun (a eta b) eta bi erreferentzia sistema inertzial ${\displaystyle v}$ abiadura erlatiboa dutenak. Gertaerak leku berberean gertatzen diren behatzailearentzat bi jazoerak ${\displaystyle t_{a}}$ eta ${\displaystyle t_{b}}$ denboretan gertatzen dira. Beste erreferentzia inertzial batean dagoen behatzaile inertzialak honako denborak ikusiko ditu:

${\displaystyle t_{a}^{\prime }={\frac {t_{a}-{\frac {vx_{a}}{c^{2}}}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}},\ t_{b}^{\prime }={\frac {t_{b}-{\frac {vx_{b}}{c^{2}}}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}}$

Leku berberean gertatzen direnez prima gabeko erreferentziarentzat ${\displaystyle x_{a}=x_{b}}$ dugu eta,

${\displaystyle \Delta t'=\gamma \Delta t={\frac {\Delta t}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}}$

non ${\displaystyle \Delta t}$ denbora propioa den, hau da, erreferentzia sistema inertzial batean dagoen behatzaileak ikusten dituen bi gertakizun kolokalen ( posizio berdinean gertatzen direnak) denbora tartea den. ${\displaystyle \Delta t}$ ${\displaystyle v}$ abiaduraz higitzen den behatzaileak ikusten duen bi gertakizunen arteko denbora tartea da. Hemen lehen bezala, gertakizunen denbora tartea desberdina da.

Hala ere, guk ez dugu honelako eraginik hautematen, argiaren abiadurara gerturatzean efektuak gero eta nabariagoak izaten dira baina abiadura oso baxuagoetan arbuiagarriak.[26]

Erlatibitate berezian, denboraren zabalkuntza normalean v abiadura erlatibo konstantearekin deskribatzen da. Hala ere, atal honetan ikusiko dugu nola Lorentzen transformazioek ahalbidetzen duten g azelerazio konstantedunak eragindako masa unitateko indarrak sortutako denbora propioa kalkulatzea ahalbidetzen duten.

Izan bitez t "geldiuneko" deituko dugun erreferentzia sisteman neurtuko den denbora, x espazio koordenatua eta X ardatza abiadura eta azelerazioaren norabidea. Demagun hasieran ${\displaystyle x=0,t=0}$ direla eta ${\displaystyle v_{0}}$ abiadura duela espazio ontzi batek.

Hasierako abiadura horrekin ${\displaystyle \gamma _{0}}$ faktorea

${\displaystyle \gamma _{0}={\frac {1}{\sqrt {1-v_{0}^{2}/c^{2}}}}}$

Posizioa ${\displaystyle t}$ denboraren menpe:

${\displaystyle x(t)={\frac {c^{2}}{g}}\left({\sqrt {1+{\frac {\left(gt+v_{0}\gamma _{0}\right)^{2}}{c^{2}}}}}-\gamma _{0}\right)}$

Abiadura:

${\displaystyle v(t)={\frac {gt+v_{0}\gamma _{0}}{\sqrt {1+{\frac {\left(gt+v_{0}\gamma _{0}\right)^{2}}{c^{2}}}}}}}$

Denbora propioa ${\displaystyle t}$ denboraren menpe:

${\displaystyle \tau (t)=\tau _{0}+\int _{0}^{t}{\sqrt {1-\left({\frac {v(t')}{c}}\right)^{2}}}dt'}$

Baldintza hauekin; ${\displaystyle v(0)=v_{0}=0,\tau (0)=\tau _{0}=0}$ integrala funtzio logaritmiko bezala edo alderantzizko funtzio hiperboliko gisa adieraz daiteke.

${\displaystyle \tau (t)={\frac {c}{g}}\ln \left({\frac {gt}{c}}+{\sqrt {1+\left({\frac {gt}{c}}\right)^{2}}}\right)={\frac {c}{g}}\operatorname {arsinh} \left({\frac {gt}{c}}\right)}$

Ontziaren denbora propioaren menpe espresioak:[27]

Posizioa:

${\displaystyle x(\tau )={\frac {c^{2}}{g}}\left(\cosh {\frac {g\tau }{c}}-1\right)}$

Abiadura:

${\displaystyle v(\tau )=c\tanh {\frac {g\tau }{c}}}$

${\displaystyle t}$ denbora propioaren menpe:

${\displaystyle t(\tau )={\frac {c}{g}}\sinh {\frac {g\tau }{c}}}$

Hipotesi honetan asumitzen da erlojuaren tik taken erritmoaren zabalkuntzak ez duela azelerazioaren menpekotasunik, aldiuneko abiaduraren menpekotasuna dauka soilik. Horren baliokidea izango litzateke P ibilbidean zehar doan erlojuak neurtzen duen denbora propioa

${\displaystyle \tau =\int _{P}{\sqrt {dt^{2}-dx^{2}/c^{2}-dy^{2}/c^{2}-dz^{2}/c^{2}}}}$

izatea.

Erlojuaren hipotesia Einsteinen 1905-ko erlatibitate berezian modu inplizituan agertzen da. Harrezkero, erlatibitateko axiometan sartua izan da.

Gorriranzko lerrakuntza grabitatorioak azaltzen du uhin elektromagnetikoak edo fotoiak putzu grabitazional batetik ateratzen saiatzen direnean, energia galtzen dutela. Energia galera hori fotoiaren maiztasuna txikitzea dakar. [29]

${\displaystyle E=h\nu ={\frac {hc}{\lambda }}}$

Gorriranzko lerrakuntza deritzo uhin luzera handiagoetara jotzen dutelako, baina aldrebes ere gerta daiteke, hau da, putzu grabitazionalaren barnealdera joatean urdineranzko lerrakuntza dugu. Fenomeno hori denboraren zabalkuntzarekin lot daiteke. Hasteko, kontuan izan behar da lehen inplizituki adierazi dena; argiari grabitateak eragiten dio. Demagun argiaren maiztasunean oinarritutako erloju bat dugula eta dorre baten behealdean kokatzen dugula. Guk dorrearen goialdean gaudenean ailegatzen zaigun argiaren maiztasuna txikiagoa da, argiak energia galdu duelako, eta hortaz geldoago mugitzen dela esango dugu. Denbora erritmo mantsoago batean igarotzen da eremu grabitazional batean murgilduta.

Iturrian uhinaren maiztasun propioa, hau da, iturria geldi dagoeneko sistema inertzial lokalean neurtua ${\displaystyle \nu _{I}}$ bada eta goialdean jasotzen dena ${\displaystyle \nu _{D}}$ bada, gorriranzko lerrakuntza[30]

${\displaystyle z={\frac {{\nu _{I}}-\nu _{D}}{\nu _{D}}}}$

Eremu grabitatorioa ahultzat har badaiteke,

${\displaystyle z\approx {\frac {\Phi (x_{D})-\Phi (x_{I})}{c^{2}}}}$

Honi buelta emanda

${\displaystyle T_{I}=T_{D}(1-{\frac {\Delta \Phi }{c^{2}}})^{-1}\approx T_{D}(1+{\frac {\Delta \Phi }{c^{2}}})}$

Zehaztasun handiko kronometrajea, Lurraren orbita baxuko sateliteen jarraipena eta pultsarren kronometrajea denboraren zabalkuntza jasaten duten prozesuak dira. Zabalkuntza hori masaren eta mugimenduaren efektu konbinatuek eragiten dute. Eguzki-sistemarako eta Lurrerako denboraren zabalkuntza efektu erlatiboak oso zehatz modelatu daitezke Einsteinen eremu ekuazioen Schwarzschild-en soluzioarekin. Schwarzschild-en metrikan, ${\displaystyle dt_{\text{E}}}$ tartea honako formulak ematen du:[31][32]

${\displaystyle dt_{\text{E}}^{2}=\left(1-{\frac {2GM_{\text{i}}}{r_{\text{i}}c^{2}}}\right)dt_{\text{c}}^{2}-\left(1-{\frac {2GM_{\text{i}}}{r_{\text{i}}c^{2}}}\right)^{-1}{\frac {dx^{2}+dy^{2}+dz^{2}}{c^{2}}}}$

• ${\displaystyle dt_{\text{E}}}$ ${\displaystyle t_{\text{E}}}$ denbora propioaren gehikuntza txiki bat da (erloju atomiko batean neur daitekeen tartea),
• ${\displaystyle dt_{\text{c}}}$ ${\displaystyle t_{\text{c}}}$ koordenatuaren gehikuntza txiki bat da ( koordenatu denbora ),
• ${\displaystyle dx,dy,dz}$ erlojuaren posizioaren, ${\displaystyle x,y,z}$,hiru koordenatuetan gehikuntza txikiak dira ,
• ${\displaystyle {\frac {-GM_{i}}{r_{i}}}}$ Auzoko masen ondoriozko Newtonen potentzial grabitatorioen batura adierazten du, erlojutik dauden kokapenaren arteko distantzietan oinarrituta ( ${\displaystyle r_{i}}$ ). Batura honek marea-potentzial guztiak barne hartzen ditu. Erlojuaren koordenatu-abiadura honela ematen da:

${\displaystyle v^{2}={\frac {dx^{2}+dy^{2}+dz^{2}}{dt_{\text{c}}^{2}}}}$

Koordenatu denbora( ${\displaystyle t_{c}}$ )masa grabitatorio guztietatik infinituki urruti eta koordenatu sisteman geldirik dagoen "erloju koordenatu" hipotetiko batean irakurriko litzatekeen denbora da ( ${\displaystyle U=0}$ eta ${\displaystyle v=0}$ ). Abiaduraren osagai erradiala duen erloju baten denbora propioaren eta koordenatu-denboraren arteko erlazio zehatza hau da:

${\displaystyle {\frac {dt_{\text{E}}}{dt_{\text{c}}}}={\sqrt {1+{\frac {2U}{c^{2}}}-{\frac {v^{2}}{c^{2}}}+\left({\frac {c^{2}}{2U}}+1\right)^{-1}{\frac {{v_{\shortparallel }}^{2}}{c^{2}}}}}={\sqrt {1-\left(\beta ^{2}+\beta _{e}^{2}+{\frac {\beta _{\shortparallel }^{2}\beta _{e}^{2}}{1-\beta _{e}^{2}}}\right)}}}$

non:

• ${\displaystyle v_{\shortparallel }}$ abiadura erradiala da,
• ${\displaystyle v_{e}={\sqrt {\frac {2GM_{i}}{r_{i}}}}}$ ihes abiadura da,
• ${\displaystyle \beta =v/c}$, ${\displaystyle \beta _{e}=v_{e}/c}$ eta ${\displaystyle \beta _{\shortparallel }=v_{\shortparallel }/c}$ c argiaren abiaduraren ehuneko gisan emandako abiadurak dira,
• ${\displaystyle U={\frac {-GM_{i}}{r_{i}}}}$ potentzial newtoniarra da; horregatik ${\displaystyle -U}$ ihes abiaduraren karratuaren erdia da.

Goiko ekuazioa zehatza da Schwarzschild-en soluzioaren hipotesien arabera. Abiadurak eragindako denbora zabalkuntza ekuaziora murrizten da higiduraren presentzian eta grabitate ezean, alegia ${\displaystyle \beta _{e}=0}$ denean. Grabitazio-denbora zabalkuntza-ekuaziora murrizten da mugimendurik ezean eta grabitatearen presentzian, hau da. ${\displaystyle \beta =0=\beta _{\shortparallel }}$ .