Catalan-en solido
Geometrian, Catalanen solidoak Arkimedesen solidoen poliedro dualak dira. Poliedro horiei Eugène Catalan belgiar matematikariak jarri zien izena; berak deskribatu zituen lehenengoz, 1865ean.
Catalanen solido guztiak ganbilak dira. Haien aurpegiak ez dira poligono erregularrak, solido platonikoetan eta Arkimedesen solidoetan ez bezala.
Sailkapena
Catalanen solidoak 13 dira (edo 15, ikositetraedro pentagonalaren eta hexakontaedro pentagonalaren bi forma kiralak kontuan hartzen baditugu).
| Izena (Aurpegi-konfigurazioa) |
Gardena | Kolore solidotan |
Garapena | Aurpegiak | Ertzak | Erpinak | Simetria-taldea |
|---|---|---|---|---|---|---|---|
| triakistetraedroa (V3.6.6) |
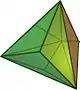 (Animazioa) |
 |
 |
12 triangelu isoszele | 18 | 8 | Td |
| dodekaedro erronbikoa (V3.4.3.4) |
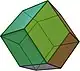 (Animazioa) |
 |
 |
12 erronbo | 24 | 14 | Oh |
| triakisoktaedroa (V3.8.8) |
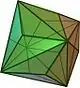 (Animazioa) |
 |
 |
24 triangelu isoszele | 36 | 14 | Oh |
| tetrakishexaedroa edo tetrahexaedroa edo hexakistetraedroa (V4.6.6) |
 (Animazioa) |
 |
 |
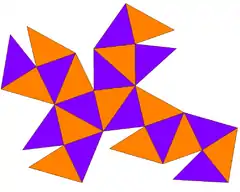24 triangelu isoszele | 36 | 14 | Oh |
| ikositetraedro trapezoidala edo ikositetraedro deltoidala (V3.4.4.4) |
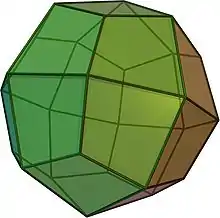 (Animazioa) |
 |
 |
24 kometa | 48 | 26 | Oh |
| hexakisoktaedroa edo disdiakisdodekaedroa (V4.6.8) |
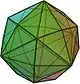 (Animazioa) |
 |
 |
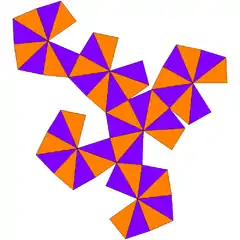48 triangelu eskaleno | 72 | 26 | Oh |
| ikositetraedro pentagonala (V3.3.3.3.4) |
  (Anim.)(Anim.) |
 |
 |
24 pentagono irregular | 60 | 38 | O |
| triakontaedro erronbikoa (V3.5.3.5) |
 (Animazioa) |
 |
 |
30 erronbo | 60 | 32 | Ih |
| triakisikosaedroa (V3.10.10) |
 (Animazioa) |
 |
 |
60 triangelu isoszele | 90 | 32 | Ih |
| pentakisdodekaedroa (V5.6.6) |
 (Animazioa) |
 |
 |
60 triangelu isoszele | 90 | 32 | Ih |
| hexakontaedro trapezoidala edo hexakontaedro deltoidala (V3.4.5.4) |
 (Animazioa) |
 |
 |
60 kometa | 120 | 62 | Ih |
| hexakisikosaedroa edo disdiakistriakontaedroa (V4.6.10) |
 (Animazioa) |
 |
 |
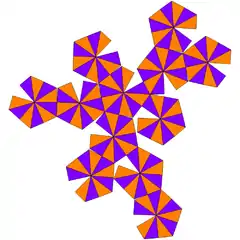120 triangelu eskaleno | 180 | 62 | Ih |
| hexakontaedro pentagonal (V3.3.3.3.5) |
  (Anim.)(Anim.) |
 |
 |
60 pentagono irregular | 150 | 92 | I |
Kanpo estekak
- (Ingelesez) Weisstein, Eric W.: "Catalan Solids" MathWorld-en.
| Autoritate kontrola |
|
|---|
Datuak: Q258921
Multimedia: Catalan solids / Q258921
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.