Brahmagupta

Brahmagupta, berak adierazi zuenez, K. o. 598. urtean jaio zen. Brahmagupta Indiako ipar-sartaldeko Bhillamalan bizi izan zen Harsharen jaurgoan. Horregatik, askotan, Bhillamalacarya (euskaraz: «Bhillamalako irakaslea») deitzen zaio. Gero Malwako Ujjaingo behatoki astronomikoko burua izan zen. Bertan matematikari eta astronomiari buruzko liburua idatzi zuen, Brāhmasphuṭasiddhānta («Egokiro Sortutako Brahmaren Jakinbidea») 628an, eta Khandakhadyaka («jateko hozka» edo «janari-mordoa») lan praktikoa 665ean. Bi liburu horien artean, Brāhmasphuṭasiddhānta da, zalantzarik gabe, garrantzitsuena.

Brahmaguptaren teoremaren diagrama.

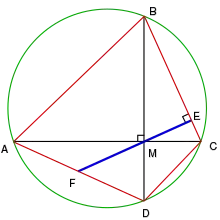
Bere lanean, hirukote pitagorikoa eratzeko araua dago:

${\displaystyle m,{\frac {m^{2}}{2(m-n)}},{\frac {m^{2}}{2(m+n)}}}$

hori Babiloniako antzinako arauaren aldaketa izan arren, berak ezin hobeto ezagutu ahal izan zuena. Laukientzako eremuaren Brahmaguptaren formula, formulekin batera erabili zuen:

${\displaystyle {\sqrt {\frac {(ab+cd)(ac+bd)}{(ad+bc)}}}}$ y ${\displaystyle {\sqrt {\frac {(ac+bd)(ad+bc)}{(ab+cd)}}}}$

diagonaletarako, zenbaki arruntak diren alde, diagonal eta eremuak dauzkaten laukiak aurkitzeko.

Brahmaguptak, jakina, matematika berez atsegin zuen, ezen praktikatik kanpoko gauzak ezartzen baitzituen, hala nola haren laukiei buruzko emaitzak. Antza denez, bera ekuazio diofantiko linealari irtenbide orokorra ematen lehena izan zen:

${\displaystyle ax+by=c}$ con ${\displaystyle a,b,c\in \mathbb {Z} }$.

Ekuazio horrek emaitzak eduki ditzan, ${\displaystyle c}$ ${\displaystyle a}$ eta ${\displaystyle b}$-ren zatitzaile komun handienaz zatitu behar da, eta Brahmaguptak bazekien, ${\displaystyle a}$ eta ${\displaystyle b}$ elkarrekiko zenbaki lehenak baldin badira, orduan, ekuazioaren emaitza guztiak honako formula hauek ematen dituztela:

${\displaystyle x=p+mb}$, ${\displaystyle y=q-ma}$

Bertan ${\displaystyle m}$ zenbaki oso arbitrarioa da.

donde ${\displaystyle m}$ es un entero arbitrario.[1][2]