Born-Oppenheimerren hurbilketa
Born-Oppenheimer hurbilketa Schrodingerren ekuazioaren ebazketa sinplifikatzeko erabiltzen da. Hau egiteko, zenbait suposizio egin behar dira ekuazioa bitan banatzeko, zati elektronikoa eta zati nuklearra izango direnak; zati bakoitzak bere esanahi fisikoa du eta modu grafiko batean irudikatu daiteke.
Mekanika kuantikoaren arabera, uhin-funtzioak sistema baten propietate guztiak definitzen ditu. Horretarako, Schrödingerren ekuazioa ebatzi behar da.
Izan ere, ekuazioa hau oso konplexua da ebazteko, eta hurbilketa bat egiten da. Hain zuzen ere, Born-Oppenheimer hurbilketa.
Horretarako, elektroiaren masa nukleoarenarekin alderatuta askoz ere arinagoa dela hartzen da kontuan (me/Mα<<10-3), eta, horrexegatik, elektroiaren eta nukleoaren mugimenduak guztiz desakoplatuak daudela kontsideratzen da.
Hurbilketa hau eginda, elektroiaren eta nukleoren menpe dagoen uhin-funtzioa bitan banatzen da: elektronikoari dagokion funtzio eta nuklearrari dagokiona.
Zati elektronikoa:
Zati nuklearra:
Zati elektronikoa
VNN (R)-ren balioa konstantea denez eta Eel (R)parametroak elektroiaren eragina adierazten duenez, energia potentzialaren gainazala definitu daiteke.
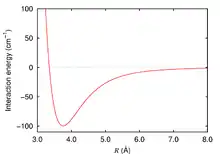
Schrödingerren ekuazioa ebazteko, nukleoarentzat posizio finko bat ematea beharrezkoa da, eta, horrela, ekuazio elektronikoa ebazten da. Behin hau eginda energia-potentziala (U) nukleoaren distantziarekiko (R) irudikatzen da. Ia grafiko guztietan minimo bat ikus daiteke; bertan, sistemak energia gutxien izango du eta honek sistemaren oreka adierazten du.
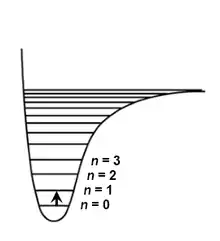
1. irudiak egoera elektroniko bakarra erakusten du (oinarrizko egoera); izan ere, molekulak egoera elektroniko bakarrean baino gehiagotan egon daitezke (2. irudia). Molekulak energia kantitate bat xurgatzen badu (hv), elektroi bat edo batzuk kitzikatu eta molekularen egoera elektronikoa aldatu egingo da. Egoera kitzikatu honek oinarrizko egoera baino energia handiago du.


3. irudian ikusten den bezala, bien arteko energia diferentzia kalkulatu daiteke. Hau horrela izanik, egoera batetik bestera pasatzeko energia zein den jakin dezakegu.
Erreakzioak aurreikusi ditzazkegu molekularen energia potentzial gainazalean oinarrituz, erreakzio koordinazio diagramak errepresentatuz. Ikus E.P.G. (energia potentzial gainazala) informazio gehiago nahi izatekotan.
Zati nuklearra
Bestetik, zati nuklearrarekin, molekularen translazio-, errotazio- eta bibrazio-energiak kalkulatu daitezke. Horretarako, espektroskopia erabiltzen da. Ikus I.G. eta espektroskopia informazio gehiago nahi izatekotan.
Erreferentziak
- D. M. Charutz, R. Baer and M. Baer, Chem. Phys. Lett. 265, 629 (1996).
- M. Baer and R. Englman, Chem. Phys. Lett. 265, 105 (1997).
- M. Born and K. Huang, Dynamical Theory of Crystal Lattices, 1954 (Oxford University Press, New York), Chapter IV.