Argi-kono

Bi gertaera izanik (${\displaystyle x_{1}^{\mu }}$ eta ${\displaystyle x_{2}^{\mu }}$), diferentzia bat definituko dugu, zeinak bien arteko denbora-tartea eta posizio erlatiboa bilduko dituen:

${\displaystyle \Delta x^{\mu }=(c\Delta t,\Delta {\textbf {x}})\equiv x_{2}^{\mu }-x_{1}^{\mu }=(c(t_{2}-t_{1}),{\textbf {x}}_{2}-{\textbf {x}}_{1})}$

Lorentzen transformazioak linealak dira, hortaz, kendurak era berean transformatzen dira:

${\displaystyle \Delta x^{\mu '}=\Lambda _{\nu }^{\mu '}\Delta x^{\nu }}$ eta ${\displaystyle \Delta x^{\mu }=\Lambda _{\nu '}^{\mu }\Delta x^{\nu '}}$

Bi gertaeren arteko espazio-denborako tartea defini daiteke:

${\displaystyle \Delta s^{2}\equiv -c^{2}\Delta t^{2}+\Delta {\textbf {x}}^{2}=-c^{2}\Delta t^{2}+\Delta {x}^{2}+\Delta {y}^{2}+\Delta {z}^{2}}$

Tarte hau positiboa, negatiboa zein nulua izan daiteke, eta bere propietate nagusia ondorengoa da: eskalarra dela. Aldaezin erlatibista denez, edozein erreferentzia-sistema inertzialetan balio bera du, hau da:

${\displaystyle \Delta s^{2}=-c^{2}\Delta t^{2}+\Delta {x}^{2}+\Delta {y}^{2}+\Delta {z}^{2}=-c^{2}\Delta {t'}^{2}+\Delta {x'}^{2}+\Delta {y'}^{2}+\Delta {z'}^{2}}$

Bere zeinuaren arabera, hiru multzotan sailka ditzakegu espazio-denborako tarteak: espazio motako tarteak, denbora motako tarteak eta argi motako tarteak.

Argi motako tarteetan soilik sakonduko dugu, horiek baitira argi-konoa definitzeko behar ditugunak. Hauetan, espazio-denborako tartea anulatu egiten da, espazio-tartea (${\displaystyle |\Delta {\textbf {x}}|}$) eta denbora-tartea (${\displaystyle c|\Delta t|}$) berdinak baitira bertan (${\displaystyle |\Delta {\textbf {x}}|=c|\Delta t|}$). Hortaz,

${\displaystyle \Delta s^{2}=\Delta {\textbf {x}}^{2}-c^{2}\Delta t^{2}=0\Longleftrightarrow \left\vert {\frac {\Delta x}{\Delta t}}\right\vert =c}$

Aipatzekoa da mota horretako tarteetan erlazio kausala egon daitekeela bi gertaeren artean, kausalitatearen printzipioa hondatu gabe.

Honela defini daiteke ${\displaystyle G_{0}=(ct_{0},x_{0},y_{0},z_{0})}$ gertaeraren argi-konoa: ${\displaystyle G_{0}}$-rekin batera espazio-denborako tarte nulu bat (argi motako tarte bat) osatzen duten puntuen leku geometrikoa. Esan bezala, espazio-denborako tarteak aldaezin erlatibistak direnez, edozein erreferentzia-sistema linealetan beteko da definizio hori, guztietan beteko baita ${\displaystyle \Delta s=0}$ ekuazioa. Baldintza hori beste era batean formula daiteke:

${\displaystyle (x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}=c^{2}(t-t_{0})^{2}}$

Bi dimentsioko irudiak egiteko, dimentsio espazial bakarra hartzen da kontuan, ${\displaystyle \Delta y=\Delta z=0}$ eginez eta argi-konoa ${\displaystyle (ct,x)}$ planoan proiektatuz. Hau da lortzen den proiekzioa:

${\displaystyle (x-x_{0})^{2}=(t-t_{0})^{2}}$

Beraz, bi dimentsioko irudietan, ${\displaystyle G_{0}}$-ren argi-konoa ${\displaystyle \pm 1}$ maldako bi lerro elkarzuten bidez adierazten da.

Aipatu dugun modura, argi-konoak irudikatzeko hiru dimentsioko irudiak egin ohi dira, hau da, bi dimentsio espazial hartu ohi dira kontuan. ${\displaystyle \Delta z=0}$ eginez, honako ekuazioak definitzen du argi-konoa ${\displaystyle (ct,x,y)}$ espazioan:

${\displaystyle (x-x_{0})^{2}+(y-y_{0})^{2}=c^{2}(t-t_{0})^{2}}$

Hiru dimentsio espazialak kontuan izanik lortu dugun adierazpen orokorrenak hiperkono bat definitzen du espazio-denboran, eta irudikatzeko garaian hiru dimentsio espazialak ez hartzearen arrazoia sinplea da, ezin dugula hiperkono bat bi dimentsio

tan marraztu.

Hasteko, tentsoreen notazioarekin berrikusiko dugu argi-konoaren definizioa.

Minkowskiren espazio-denboran, metrika laua dugunez, koordenatu sistema jakin bat existitzen da, kasu honetan, Minkowskiren koordenatu-sistema, zeinetan metrika diagonala den, ${\displaystyle \pm 1}$ balioekin. Honela idazten dira koordenatuak:

${\displaystyle (x^{\mu })=(x^{0},x^{1},x^{2},x^{3})=(t,x,y,z)}$

Lehen ikusi dugun bezala:

${\displaystyle ds^{2}=dt^{2}-dx^{2}-dy^{2}-dz^{2}}$

Hau forma tentsorialean berridatz daiteke:

${\displaystyle ds^{2}=\eta _{ab}dx^{a}dx^{b}}$, non ${\displaystyle \eta _{ab}={\mathsf {diag}}(1,-1,-1,-1)}$

Koordenatu-sistema orokorrago batean:

${\displaystyle ds^{2}=g_{ab}dx^{a}dx^{b}}$

Minkowskiren espazioan, bektore baten karratua honela defini ohi da:

${\displaystyle X^{2}=g_{ab}X^{a}X^{b}=X_{a}X^{a}}$

Bere zeinuaren arabera, espazio motakoa, denbora motakoa edo argi motakoa (nulua) izango da. Jarritako adierazpenean, agerikoa da bektore nulu bat bere buruarekiko ortogonala dela; eta Minkowskiren espazioko P puntu batean, bektore nuluen multzoak kono nulua edo argi-konoa osatzen du.

${\displaystyle T^{a}}$ denbora motako bektorea Minkowskiren koordenatuetan ${\displaystyle T^{a}=(1,0,0,0)}$ erara definitzen badugu, honela sailkatu ohi da:

• Etorkizuneranzkoa, ${\displaystyle \eta _{ab}X^{a}T^{b}>0}$ bada
• Iraganeranzkoa, ${\displaystyle \eta _{ab}X^{a}T^{b}<0}$ bada

Etorkizuneranzko denbora motako bektore guztiak etorkizuneko argi-konoaren baitan daude, iraganeranzko guztiak iraganeko argi-konoaren barnean dauden bitartean.

Denbora motako unibertso-lerro bat ondorengoa da: kurba bat zeinaren bektore tangentea beti denbora motakoa den. Zehazki, kurba hori geodesiko bat bada, denbora motako geodesiko deritzo. Denbora motako unibertso-lerroek partikula materialek jarrai ditzaketen ibilbideak mugatzen dituzte.

Horrela, G gertaeraren argi-konoaren definizioa birformula daiteke: Gwh puntutik igarotzen diren geodesiko nulu guztien multzoa izango litzateke.

Grabitazio leiar baten animazioa

Erlatibitate orokorrak zera esaten diosku, argiaren ibilbidea desbideratua izan daitekeela eremu grabitatorio baten ondorioz. Are, masak espazioa kurba dezakeela erakusten du erlatibitate orokorrak. Jon Archibald Wheeler-ek esan zuen bezala:

Materiak espazioari nola kurbatu esaten dio, eta espazioak materiari esaten dio nola mugitu.[8]

Argiak geodesiko nuluak jarraitzen ditu. Egun, badakigu kualitatiboki bat datozela behaketa esperimentalak Einteinen proposamenarekin. Horren erakusle dira grabitazio leiarrak.

Esan bezala, behatzaileok denbora motako unibertso-lerro batean higitzen gara, zeinaren noranzkoa edozein puntutan etorkizuneko argi-konoaren baitan dagoen halabeharrez.

Hasteko, funtsezko ideia bat azpimarratuko dugu: kurbatutako espazio-denboran, argi-konoak zenbait eratara eraldatuak izan daitezke, eta baita haien orientazioa aldatu ere.

Schwarzschilden soluzioa, Schwarzschilden koordenatuetan (dimentsio espazial bakarra kontuan hartuz)

Alboko irudian Schwarzschilden soluzioa dago irudikatuta dimentsio espazial bakarrarekin, Schwarzschilden koordenatuetan. Honako hau dugu Schwarzschilden soluzioa:

${\displaystyle ds^{2}=(1-2m/r)dt^{2}-(1-2m/r)^{-1}dr^{2}-r^{2}(d\theta ^{2}+\sin ^{2}\theta d\phi ^{2})}$

Zenbait ondorio interesgarri ikus daitezke bertan. Espero genezakeen bezala, ${\displaystyle r}$ oso handietarako, geodesiko nuluek ${\displaystyle 45^{\circ }}$-ko angeluak osatzen dituzte gure ardatzekin, soluzioa asintotikoki laua baita. Ezkerreko sekzioan, singularitatetik gertu, argi-kono lokalak inklinatu egiten dira, esan daiteke ${\displaystyle t}$ eta ${\displaystyle r}$ koordenatuek haien artean izaera trukatu egiten dutela. Ezkerreko zonaldean, behatzaile batek ezin du denboran ${\displaystyle r}$-ren balio konstante bat izan, singularitate intrintsekorantz mugitzera dago kondenatuta, zonalde horretako etorkizuneko argi-konoetan ikus daitekeen bezala. Diagrama honen arabera, badirudi eskuineko zonaldean dagoen eta singularitaterantz higitzen ari den behatzaile batek denbora infinitua beharko lukeela irudian seinalatuta dagoen Schwarzschilden erradiora iristeko. Baina, diagrama honek engainua eragiten du: ${\displaystyle r}$ handietan dagoen behatzaile batentzat, ${\displaystyle t}$ koordenatua erabilgarria da, eta esanahi fisikoa dauka; bere ikuspegitik, singularitatera hurbiltzen ari den gorputz batek denbora infinitua beharko du Schwarzschilden erradiora iristeko. Baina, erradialki hurbiltzen ari den gorputzaren ikuspegitik, bai Schwarzschilden erradiora zein ${\displaystyle r=0}$-ra irits daiteke denbora finituan.

Beraz, Schwarzschilden ${\displaystyle t}$ koordenatua desegokia dela ondoriozta daiteke (higidura honen deskribapenean).

Ideia sinplea da: denbora-koordenatu berri bat aukeratuko dugu, zeinetan singularitaterantz zuzendutako geodesiko nulu erradialak lerro zuzenak bilakatzen diren.

Schwarzschilden soluzioa, Eddington eta Finkelsteinen koordenatuetan

Ondorengo aldaketa eginez,

${\displaystyle t\rightarrow {\bar {t}}=t+2m\ln(r-2m)}$

Honako soluzioa lortzen dugu (${\displaystyle dt}$ Scharzschilden soluzioan sartuz):

${\displaystyle ds^{2}=(1-{\frac {2m}{r}})d{\bar {t}}^{2}-{\frac {4m}{r}}d{\bar {t}}dr-(1+{\frac {2m}{r}})dr^{2}-r^{2}(d\theta ^{2}+\sin ^{2}\theta d\phi ^{2})}$

Soluzio hau erregularra da ${\displaystyle r=2m}$ denean, eta koordenatuak egokiak diren zonaldea ${\displaystyle 0<r<\infty }$ tartera handitu da (${\displaystyle 2m<r<\infty }$ ordez). Koordenatu hauetan, espazio-denborako diagramak itxura ezberdina hartzen du, irudian ikusten den moduan. ${\displaystyle r}$ oso handietan, argi-konoek, aurreko kasuan bezala, ${\displaystyle 45^{\circ }}$-ko angelua osatzen dute. Kasu honetan, argi-konoen ezkerreko aldeari erreparatuz (gorriz, irudian) ikusten da ${\displaystyle r}$ ardatzarekiko ${\displaystyle -45^{\circ }}$-ko angelua osatzen dutela guztiek. Aldiz, eskubiko aldeei dagokienez (urdinez), ${\displaystyle 45^{\circ }}$-etan hasten dira ${\displaystyle r}$ handietan, baina barrurantz inklinatzen dira ${\displaystyle r}$ txikiagotu ahala (${\displaystyle r=2m}$ denean, bertikala da, eta hortik aurrera, ezkerrera inklinatutakoa). Azpimarratzekoa da ${\displaystyle r=2m}$ denean, kanpora doazen fotoiak dauden lekuan mantentzen direla.

${\displaystyle r=2m}$ gainazalak alde bakarreranzko mintz baten papera jokatzen du: etorkizuneranzko denbora motako kurbak eta kurba nuluak soilik kanpotik barrura igarotzen utziz. Etorkizuneranzko kurba nulu batek ere ezin du ihes egin bertatik. Beraz, honelako gainazalek gertaera-horizonte izena hartzen dute. Ondorengoa adierazten dute: kanpoko behatzaile inertzial batek beha dezakeenaren muga. Absolutua da gertaera-horizonte hori.

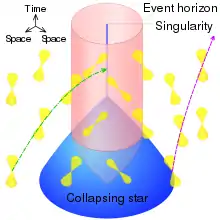
Oso labur azalduta, hurrengo egoeran sortzen dira zulo beltzak; izarren kolapsoa hain handia denean zeinen eta efektu grabitatorioek barneko presioarenak gainditzen dituzten.

Izarrak guztiz esferiko dirauen bitartean, kanpoko eremua Schwarzschilden soluzioak ematen digu. Demagun kolapsatzen ari den izarraren gainazalean behatzaile bat dagoela, denbora-tarte erregularretan seinaleak igortzen (bere ikuspegitik). Orduan, urruneko behatzaile batek gero eta denbora tarte handiagoarekin jasoko ditu seinaleak. ${\displaystyle r=2m}$ denean bidalitako seinaleak ez du inoiz bertatik ihes egitea lortuko, eta horren ondoren igorritako guztiak singularitaterantz erakarriak izango dira. Urruneko behatzaileak itxaroten duen denbora edozein delarik ere, ez du lortuko izarra nolakoa den ikustea justu izarrak Schwarzschilden erradioa izatera iritsi aurretiko momentuaz geroztik. Praktikan, hala ere, urruneko behatzaileak denbora gutxi barru ezin izango du izarraren gainazala ikusi ere egin, gorriranzko lerrakuntza handiaren ondorioz.

Zulo beltzen, edo kolapso grabitatorioaren, inguruko argi-konoen bilakaera ikus daiteke alboko irudian, emandako azalpena bisualki ikusteko helburuz.