Anscomberen laukote
Anscomberen laukotea ezaugarri estatistiko berdinak dituzten lau datu multzo dira, baina grafikoki aztertu ondoren, argi eta garbi erakusten dutenak datu multzo ezberdinak direla. Francis Anscombe estatistikariak asmatu zituen 1973garren urtean, datuak aztertu aurretik datu diagramak eratzeko beharra erakutsi eta azterketa kuantitatiboaren mugak agerian uzteko. Halaber, muturreko datuen eraginaz ere ohartarazi nahi zuen.
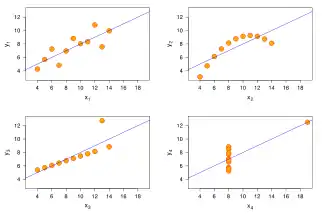
Anscombe-ren laukotea osatzen duten lau datu multzoen sakabanatze diagramak
Lau datu multzoen azterketa estatistikoaz emaitza hauek lortzen dira, berdinak lau datu multzoetarako, harrigarria bada ere, datu multzoak ezberdinak baitira:
| Neurria | Balioa |
|---|---|
| aldagaien batez bestekoa | 9.0 |
| aldagaien bariantza | 10.0 |
| aldagaien batez bestekoa | 7.5 |
| aldagaien bariantza | 3.75 |
| Korrelazioa x eta y artean | 0.816 |
| Erregresio zuzena |
Lau datu multzoak ondoren zehazten dira:
| I | II | III | IV | ||||
|---|---|---|---|---|---|---|---|
| x | y | x | y | x | y | x | y |
| 10.0 | 8.04 | 10.0 | 9.14 | 10.0 | 7.46 | 8.0 | 6.58 |
| 8.0 | 6.95 | 8.0 | 8.14 | 8.0 | 6.77 | 8.0 | 5.76 |
| 13.0 | 7.58 | 13.0 | 8.74 | 13.0 | 12.74 | 8.0 | 7.71 |
| 9.0 | 8.81 | 9.0 | 8.77 | 9.0 | 7.11 | 8.0 | 8.84 |
| 11.0 | 8.33 | 11.0 | 9.26 | 11.0 | 7.81 | 8.0 | 8.47 |
| 14.0 | 9.96 | 14.0 | 8.10 | 14.0 | 8.84 | 8.0 | 7.04 |
| 6.0 | 7.24 | 6.0 | 6.13 | 6.0 | 6.08 | 8.0 | 5.25 |
| 4.0 | 4.26 | 4.0 | 3.10 | 4.0 | 5.39 | 19.0 | 12.50 |
| 12.0 | 10.84 | 12.0 | 9.13 | 12.0 | 8.15 | 8.0 | 5.56 |
| 7.0 | 4.82 | 7.0 | 7.26 | 7.0 | 6.42 | 8.0 | 7.91 |
| 5.0 | 5.68 | 5.0 | 4.74 | 5.0 | 5.73 | 8.0 | 6.89 |
Kanpo estekak
| Autoritate kontrola |
|
|---|
Datuak: Q2554672
Multimedia: Anscombe's quartet / Q2554672
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.