Angelu (geometria)

Sistema hirurogeitar edo sexagesimalean, zirkunferentzia oso bat inguratzen duen angelua 360 gradu sexagesimaleko neurria du (360° idazten da). Horrela, angeluko arkuak zirkunferentzia osoa hartzen duenean angeluaren neurria 2π radianekoa denez, hiruko erregela sinple batez frogatzen da, sistema hirurogeitarrera aldatzeko ${\displaystyle s/r\,}$ erlazioari biderkatu beharreko konstantea ${\displaystyle k={\frac {2\pi }{360}}}$ dela.

Horrela, adibidez ${\displaystyle 3\pi /2\,}$ radianeko angeluaren neurria, sistema hirurogeitarrean, ${\displaystyle (\pi /2)\times (360/2\pi )=90\,}$ gradukoa da [2].

Sistema ehundarrean, angelu zuzenaren neurria 100 gradu ehundarrekoa (100^g idazten da) da (sistema sexagesimalean 90° da). Zirkulu osoko angelua 400 gradu (400^g) du. Radianak gradu ehundarretara bihurtzeko biderkatu beharreko konstantea ${\displaystyle k={\frac {2\pi }{400}}}$.

• Puntua, itsasketan erabiltzen da eta zirkulu osoaren 1/32 hartzen du. Angelu zuzen batek, beraz, 8 puntu ditu.
• Ordu-angelua, astronomian erabiltzen da eta zirkulu osoaren 1/24 hartzen du. Beraz, 1 ordu = 360/12=15° = π/12 rad.

180°ko zabalera duen angelu-garraiagailua, sistema hirurogeitarrean.

Eskuz, angelu-garraiagailua erabiliz neurtzen dira angeluak. Zirkulu edo zirkulu-erdi graduatu batez osaturik, angelu-garraiagailuaren jatorria angeluaren zuzenerdi baten gainean kokatuz, garraiagailuak beste zuzenerdian adierazten duen balioa izango da angeluaren neurria.

Urrutiko objektuek osatzen duten angeluen neurria besoa luzatuz hurbildu daiteke[3][4]:

• Hatz txikiaren zabalera betetzen duen objektu baten angelua da 1.5° da gutxi gorabehera.
• Hatz txikia eta ondoko bi hatzak batera jarriz, hiru hatzak betetzen dituen zabalera duen angeluaren neurria 5° da gutxi gorabehera.
• Eskua ixten bada, erpurua barrura sartuz, ukabila betetzen duen angeluaren neurria 10° da gutxi gorabehera.
• Hatz erakuslea eta hatz txikia luzatzen badira, tartekoak bilduz, bien arteko angelua 20° da gutxi gorabehera.

Gainera, eguzkiak eta ilargiak zeruan hartzen duten eremuak osatzen duen angelua 0.5° da gutxi gorabehera.

• 90 gradu hirurogeitarreko (π/2 rad edo 100 gradu ehundar) angeluari angelu zuzen deritzo.Angelu honen bi aldeak, perpendikularrak dira elkarren artean.
• Angelu zuzena baino neurri txikiagoa duten angeluei angelu zorrotz deritze, hau da angelua 0º-90º artean dago.
• 180 gradu hirurogeitarreko (π rad edo 200 gradu ehundar) angeluari angelu lau edo angelu lerrokide deritzo.
• Angelu zuzenetik angelu laurako bitarteko neurria duten angeluei (90°-180°) angelu kamuts deritze.
• Angelu osoa zirkulu osoa hartzen duten angelua da (360°, 2π rad edo 400 gradu ehundar).
• Angelu nulua 0° edo 0 rad neurria duena da.
• Bi zuzenerdik bi angelu sortzen dute: angelu ganbila (edo sarkorra) eta angelu ahurra (edo irtenkorra). Angelu ganbila 180°tik beherakoa da. Angelu ahurra 180°tik gorakoa da.

• 
  Angelu zuzena
• 
  Angelu zorrotza
• 
  Angelu laua
• 
  Angelu kamutsa
• 
  Angelu osoa
• 
  Angelu ganbila edo sarkorra
• 
  Angelu ahurra edo irtenkorra

Bi angelu beraien artean duten erlazioari buruz, zenbait angelu mota ezartzen da:

• Ondoz-ondoko angeluak, alde komun bat dutenak dira, beste biek zuzen bat osatzen ez badute.
• Angelu osagarriak, hauen neurrien batura 90° edo ${\displaystyle \pi }$/2 radian dutenak dira. Angelu baten angelu osagarria biak batera angelu zuzen osatzeko behar den hura da.
• Angelu betegarriak, hauen neurrien batura 180° edo ${\displaystyle \pi }$ radian dutenak dira. Angelu baten angelu betegarria biak batera angelu lau bat osatzeko behar den hura da.
• Angelu konjugatuak, hauen neurrien batura 360° edo 2${\displaystyle \pi }$ radian dutenak dira.
• Angelu kongruenteak, (edo isometrikoak) zabalera bera dutenak dira , hau da, neurri berdina dutenak.
• Erpinez aurkako angeluak, angelu bateko zuzenerdiak besteko zuzenerdien luzapenak dira. Erpinez aurkako angeluak kongruenteak dira.

• 
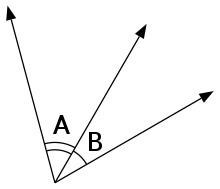  A et B ondoz ondoko angeluak dira.
• 
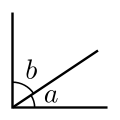  a eta b angelu osagarriak dira.
• 
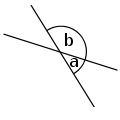  α eta β angelu betegarriak dira.
• 
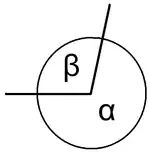  α eta β angelu konjugatuak dira.
• 
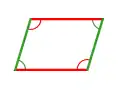  Paralelogramo bateko aurkako angeluak kongruenteak dira.
• 
  α y β erpinez aurkako angeluak dira, eta beraz, kongruenteak ere bai.

Angelu positibo eta angelu negatibo bat trigonometrian erabiltzen den zirkunferentzia goniometriko batean.

Geometrian, angelu guztiak positiboak dira: beren neurria, zuzenerdien arteko arkuaren luzera absolutua da. Trigonometrian ordea, angeluko arkua biratzeko norabidea kontuan hartzen da. Arkua erlojuko orratzen aurkako zentzuan biratzen bada, angeluaren neurria positiboa da.

Angeluko arkua erlojuko orratzen berezko zentzuan biratzen bada, angeluaren neurria negatiboa izango da. Aldiz, orratzen kontrako noranzkoan biratzean, angelua postiboa dela esaten da.

Poligono batean, barne angelua ondoz ondoko aldeek barnerantz osaturikoa da. Kanpo angelua, berriz, alde batek eta beste baten kanporako luzapenak osaturikoa da. Poligonoko erpin bateko barne angelua eta kanpo angelua betegarriak dira. Aurkako angeluak alde edo zuzenerdi komunik ez duten haiek dira.

Triangelu batek hiru barne angelu ditu: α, β eta γ. Triangelu batean ez dago aurkako angelurik.

β, β', δ eta δ' poligonoko kanpo angeluak dira. α eta β zein α eta β' angelu betegarriak dira gainera. α eta γ aurkako angeluak dira.

Angelu zentrala (berdez), angelu inskribatua (urdinez), angelu erdi-inskribatua (gorriz) eta kanpo angelua (marroiz).

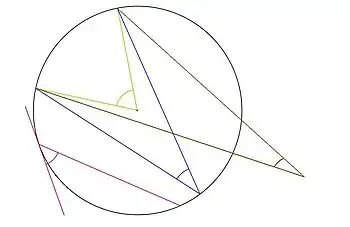
Zirkunferentzia batean zenbait angelu mota era daiteke:

• Angelu zentrala, erpina zirkunferentziaren zentroan duen hura da. Angelu zentralaren zabalera angeluak hartzen duen zirkunferentzia arkuaren zabaleraren berdina da.
• Angelu inskribatua, erpina zirkunferentziako puntu batean izan eta bere zuzenerdiek zirkunferentziako beste bi puntu ebakitzen dituen hura da. Angelu inskribatuaren zabalera angeluak hartzen duen zirkunferentzia arkuaren zabaleraren erdia da.
• Angelu erdi-inskribatua, erpina zirkunferentziako puntu batean izan, zuzenerdi batek zirkunferentziako puntu bat ebaki eta bestea erpinean bertan zirkunferentziaren tangentea den angelu hura da. Angelu inskribatuaren zabalera angeluak hartzen duen zirkunferentzia arkuaren zabaleraren erdia da.

Barruko angeluen neurria dagozkien angelu zentralenen arabera.
Irudi honen barrukoa euskaraz ikusten ez baduzu zure ordenagailuan euskara hizkuntza lehenetsia ez izateagatik izan daiteke.

• Barne angelua, erpina zirkunferentziak osatzen duen zirkuluaren barnean duenean deritzo. Barne angeluaren zabalera angeluak berak osatzen duen arkuaren zabaleraren eta erpinez aurkako angeluak osatzen duen arkuaren zabaleraren baturaren erdia da.
• Kanpo angelua, erpina zirkunferentziatik kanpo duen hura da. Bere zabalera zirkunferentzian osatzen dituen bi arkuen zabaleren kendura da.

Txandakako angeluak[5] planoko bi zuzen beste zuzen batek ebakitzen dituenean sortzen dira. Txandakako angeluak bi motakoak dira: txandakako barne angeluak eta txandakako kanpo angeluak.

Txandakako barne angeluak: zuzenak paraleloak direnean, α eta β angeluak kongruenteak dira.

Txandakako kanpo angeluak: zuzenak paraleloak direnean, α eta β angeluak kongruenteak dira.

• Angelu esferikoa esfera baten azaleran bi zirkulu maximok osatzen duten angelua da.
• Angelu diedroa ertz komun bat duten bi planoerdik osatzen duten bi angeluetatik txikiena da. Ikus Angelu diedro.
• Eulerren angeluak espazioan puntu baten koordenatuak erreferentzia sistema batetik bestera aldatzeko behar diren angeluak dira.

• 
  Triangelu esferiko batean hiru angelu esferiko daude.
• 
  Angelu diedro zuzen bat.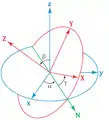
• 
  Bi sistema ortogonal ezberdin. Koordenatuak batetik bestera aldatzeko Eulerren angeluak erabiltzen dira: α, β y γ.

Astronomian, angeluak argizagiak zeruan zehatz kokatzeko erabiltzen dira, koordenatu sistema ezberdinetan. Adibidez, azimuta ostertzean argizagiaren proiekzioak iparretik osatzen duen angelua da. Paralaxia behatzaile batek bere kokapena aldatzean argizagiaren kokapena zeruan erakusten duen angelu aldaketa da.

Itsasketan, haize-angelua haizeak belaontziaren norabidearekin osatzen duen angelua da. Norabide-angelua ipar-hego norabidearekin ontziak daraman norabideak osatzen duen angelua da.

Optikan, eremu-angelua begiak sistema optiko batean hartzen dituen objektuek hartzen duten angelua da. Errefrakzio-, islatze- eta intzidentzia-angeluak izpiek osatzen dituzten angeluak dira.