Zonopluredro estas konveksa pluredro ĉe kiu ĉiu edro estas plurlatero kun punkta simetrio aŭ, ekvivalente, simetrio sub turnadoj tra 180°.

Ĉiu zonopluredro povas ekvivalente esti priskribita kiel la sumo de Minkowski de aro de segmentoj en tri-dimensia spaco, aŭ kiel la tri-dimensia paralela projekcio de pli alte dimensia hiperkubo.

Pli ĝenerale, en ĉiu dimensio, la sumo de Minkowski de segmentoj formas hiperpluredron nomata kiel zonohiperpluredro.

Zonopluredroj kiuj kahelas spaco

La originala motivado por studantaj zonopluredroj estas tio ke la figuro de Voronoi de ĉiu krado formas konveksan uniforman kahelaron de eŭklida 3-spaco en kiu la ĉeloj estas zonopluredroj. Ĉiu zonopluredro tiel formita povas kaheli 3-dimensian spacon kaj estas unueca paralelopluredro. Ĉiu unueca paralelopluredro estas kombina ekvivalento al unu el kvin specoj: kubo, seslatera prismo, senpintigita okedro, romba dekduedro, rombo-seslatera dekduedro.

Zonopluredroj de sumoj de Minkowski

Estu {v0, v1, ...} kolekto de tri-dimensia vektoroj. Kun ĉiu vektoro vi oni povas asociigi strekon {xivi|0≤xi≤1}. La sumo de Minkowski {Σxivi|0≤xi≤1} formas zonopluredron, kaj ĉiu zonopluredro kiu enhavas la fonton (0,0,0) povas esti prezentita en ĉi tiu formo. La vektoroj de kiuj la zonopluredro estas formita estas ĝiaj generiloj. Ĉi tiu difino de zonopluredroj povas facile esti ĝeneraligita al pli altaj dimensioj, donante zonohiperpluredrojn.

Ĉiu latero de zonopluredro estas paralela al almenaŭ unu el la generiloj, kaj havas longon egalan al sumo de longoj de generiloj al kiu ĝi estas paralela. Pro tio, per elekto de aro de generiloj sen paralelaj paroj de vektoroj, kaj per elekto de ĉiuj vektoroj de egala longo, oni povas formi egallateran versio de ĉiu kombina speco de zonopluredro.

La sumo de Minkowski de du zonopluredroj estas la alia zonopluredro, generita per la unio de la generiloj de la du donitaj zonopluredroj. Tiel, la sumo de Minkowski de kubo kaj senpintigita okedro estas la granda rombokub-okedro, la sumo de Minkowski de la kubo kaj la romba dekduedro estas la senpintigita romba dekduedro, de la sumo de Minkowski de la kubo, senpintigita okedro kaj romba dekduedro estas senpintigita malgranda rombokub-okedro.

Specoj de zonopluredroj

Zonopluredro estas simpla se tri edroj kuniĝas je ĉiu vertico.

Per elekto de aro de vektoroj kun alta grado de simetrio, oni povas formi zonopluredron kun same multaj simetrioj. Ekzemple, se generiloj estas egale spacita laŭ ekvatoro de sfero, kaj ankaŭ la alia paro de generiloj estas tra la polusoj de la sfero, la rezultanta zonopluredro estas prismo kun regulaj 2k-lateroj kiel bazoj: kubo, seslatera prismo, oklatera prismo, deklatera prismo, dekdulatera prismo, kaj tiel plu. Noto ke ĉi tie ĉiuj generiloj estas en paralelaj paroj, kaj do duonon el ili eblas forigi. Tiam la zonopluredro havas je (0,0,0) ne centron sed verticon, sed ĝi estos same simetria, kvankam la simetriaksoj estos jam ne tra (0,0,0) sed tra la nova centro de la zonopluredro.

Generiloj paralelaj al la lateroj de okedro formas senpintigitan okedron, kaj generiloj paralelaj al la longaj diagonaloj de kubo formas romban dekduedron.

Estas tri arĥimedaj solidoj kiuj estas zonopluredroj, ĉiuj el ili estas entutotranĉoj de la regula formoj:

Du katalanaj solidoj estas zonopluredroj:

Aliaj kun ĉiuj rombaj edroj:

Zonopluredro Regulaj edroj Edro-transitiva Latero-transitiva Vertico-transitiva Sole formas ĉelo-transitivan kahelaron Kvanto de generiloj
Kubo
4.4.4		 jes jes jes jes jes (kuba kahelaro) 3
Seslatera prismo
4.4.6		 jes ne ne jes 4
2n-prismo (n>3)
4.4.2n
(n=4)		 jes ne ne jes ne n+1
Senpintigita okedro
4.6.6		 jes ne ne jes jes (dutranĉita kuba kahelaro)
Granda rombokub-okedro
4.6.8		 jes ne ne jes ne
Granda rombo-dudek-dekduedro
4.6.10		 jes ne ne jes ne
Romba dekduedro
V3.4.3.4		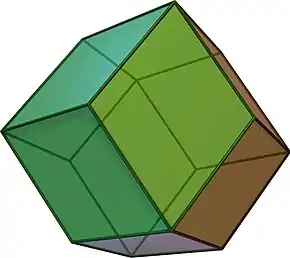 ne jes jes ne jes (romba dekduedra kahelaro)
Romba tridekedro
V3.5.3.5		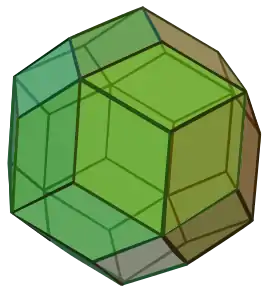 ne jes jes ne ne 6
Rombo-seslatera dekduedro ne ne ne ne jes 5
Senpintigita romba dekduedro 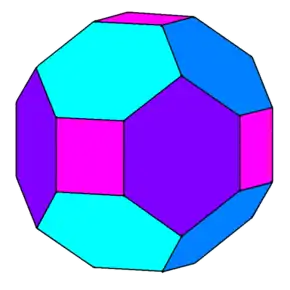ne ne ne ne ne

Sekco de zonopluredroj

Ne estas ĝenerale vero ke ĉiuj du pluredroj havas sekcon en ĉiun la alian samvolumenan pluredron (vidu en hilberta tria problemo). Tamen ĉiuj du zonopluredroj de egala volumenoj povas esti sekcita unu en la alian.

Referencoj

Zonopluredroj estis originale difinitaj kaj studitaj de Evgraf Stepanoviĉ Fjodorov.

  • Harold Scott MacDonald Coxeter (1962). “The Classification of Zonohedra by Means of Projective Diagrams - La klasifiko de zonopluredroj laŭ projekciaj figuroj”, J. Math. Pures Appl. 41, p. 137–156.
  • Eppstein, David (1996). “Zonohedra and zonotopes - Zonopluredroj kaj zonohiperpluredroj”, Mathematica in Education and Research - Mathematica en klerigado kaj esploro 5 (4), p. 15–21.
  • Grünbaum, Branko. (1972) Arrangements and Spreads - Ordigoj kaj disvastigoj. Numero 10 en Regional Conf. Series in Mathematics, American Mathematical Society.
  • Fedorov, E. S. (1893). “Elemente der Gestaltenlehre”, Zeitschrift für Krystallographie und Mineralogie 21, p. 671–694.
  • Shephard, G. C. (1974). “Space-filling zonotopes - Spaco-enspacantaj zonohiperpluredroj”, Mathematika 21, p. 261–269.
  • Taylor, Jean E. (1992). “Zonohedra and generalized zonohedra - Zonopluredroj kaj ĝeneraligitaj zonopluredroj”, American Mathematical Monthly - Amerika Matematiko Monate 99, p. 108–111. doi:10.2307/2324178.

Eksteraj ligiloj

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.