
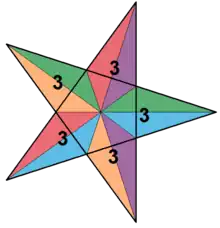
En geometrio vertica figuro estas la figuro vidata kiam angulo de pluredro aŭ hiperpluredro estas tranĉita for.
Difinoj
Prenu iun verticon de pluredro. Marku punkton ie en ĉiu latero koneksa al la vertico. Desegnu liniojn tra la koneksaj edroj, kunigante najbarajn punktojn. Post ĉi tio, ĉi tiuj linioj formas ĉenon, kiu estas plurlatero, ĉirkaŭ la vertico. Ĉi tiu plurlatero estas la vertica figuro.
Inter matematikistoj ne estas plena konsento pri la formala difino.
- Coxeter (1948, 1954) varias sian difinon kiel estas oportune por la aktuala areo de diskuto.
- Cromwell (1999) traktas ĝin kiel sferan plurlateron sur sfero centrita je la vertico.
- Skilling (1975) kaj plej abstraktaj teoriistoj uzas la difino diskutitan pli sube.
Ĝeneralaj propraĵoj
Vertica figuro prezentas la ordigon de koneksa aro de punktoj de ĉiuj najbarantaj verticoj, en hiperpluredro al donita vertico. Ĉi tio aplikas egale bone al malfiniaj kahelaroj (al spaco-enspacantaj kahelaroj) kun hiperpluredraj kiel eroj de la kahelaro.
Vertica figuro por n-hiperpluredro estas (n-1)-hiperpluredro. Ekzemple, vertica figuro por pluredro estas plurlatero, kaj la vertica figuro por 4-hiperpluredro estas pluredro.
Per konsidero de la konekseco de ĉi tiuj najbarantaj verticoj, la vertica figuro ((n-1)-hiperpluredro), povas esti konstruita por ĉiu vertico de hiperpluredro:
- Ĉiu vertico de la vertica figuro koincidas kun vertico de la originala hiperpluredro.
- Ĉiu latero de la vertica figuro ekzistas sur aŭ ene de edro de la originala hiperpluredro konektanta du malsamajn verticoj de originala edro.
- Ĉiu edro de la vertica figuro ekzistas sur aŭ ene ĉelo de la originala n-hiperpluredro (por n>3).
- ...kaj tiel plu al eroj de pli alta ordo en hiperpluredroj de pli alta dimensioj.
Verticaj figuroj estas la plej utilaj por uniformaj hiperpluredroj ĉar unu vertica figuro povas priskribi la tutan hiperpluredron.
Por pluredroj, la vertica figuro povas esti prezentita per skribmaniero de vertica konfiguro listante la edroj en vico ĉirkaŭ la vertico. Ekzemple 3.4.4.4 estas vertico kun unu triangulo kaj 3 kvadratoj, kaj ĝi prezentas la rombokub-okedron.
Se la hiperpluredro estas vertico-transitiva, la vertica figuro ekzistas en hiperebena surfaco de la n-spaco. Ĝenerale la vertica figuro ne nepre estas ebena.
Ĉe nekonveksaj pluredroj la vertica figuro povas esti ankaŭ nekonveksa. Uniformaj hiperpluredroj povas havi stelajn edrojn kaj verticajn figurojn ekzemple.
Konstruo de Dorman-Luke
Por uniforma pluredro, la edro de la duala pluredro povas esti konstruita de vertica figuro de la originala pluredro per uzo de la konstruo de Dorman-Luke.
Regulaj hiperpluredroj
Se hiperpluredro estas regula, ĝi povas esti prezentita per simbolo de Schläfli. Tiam kaj la ĉelo kaj la vertica figuro povas esti facile ekstraktitaj el ĉi tiu skribmaniero.
Ĝenerale regula hiperpluredro kun simbolo de Schläfli {a,b,c,....,y,z} havas ĉelojn {a,b,c,...,y}, kaj verticajn figurojn {b,c,...,y,z}.
- Por regula pluredro {p,q}, la vertica figuro estas {q}, q-graduso.
- Ekzemple, la vertica figuro por kubo {4,3}, estas la triangulo {3}.
- Por regula 4-hiperpluredro aŭ spaco-enspacanta kahelaro {p,q,r}, la vertica figuro estas {q,r}.
- Ekzemple, la vertica figuro por hiperkubo {4,3,3}, la vertica figuro estas regula kvaredro {3,3}.
- Por kuba kahelaro {4,3,4}, la vertica figuro estas regula okedro {3,4}.
Ĉar ankaŭ la duala hiperpluredro de regula hiperpluredro estas regula kaj prezentita per la simbolo de Schläfli kun indeksoj en la mala ordo, videblas ke la dualo de la vertica figuro estas la ĉelo de la duala hiperpluredro.
Ekzemplo de vertica figuro de kahelaro

La vertica figuro de senpintigita kuba kahelaro estas neuniforma kvadrata piramido. Unu okedro kaj kvar senpintigitaj kuboj kuniĝas je ĉiu vertico por formi spaco-enspacanta kahelaron.
| Vertica figuro: neuniforma kvadrata piramido |  |
| Kreita kiel kvadrata bazo de okedro |  |
| Kaj kvar izocelaj triangulaj - flankoj de senpintigitaj kuboj |  |
Vidu ankaŭ
- Vertica konfiguro
- Listo de uniformaj kahelaroj
- Listo de uniformaj pluredroj
- Listo de regulaj hiperpluredroj
Referencoj
- H.S.M. Coxeter, Regulaj hiperpluredroj, Hbk (1948), ppbk (1973).
- H.S.M. Coxeter (et al), Uniformaj pluredroj, Phil. Trans. 246 A (1954) pp. 401-450.
- P. Cromwel, Pluredroj, CUP pbk. (1999).
- H.M. Cundy kaj A.P. Rollett, Matematikaj modeloj, OUP (1961).
- J. Skilling, La plena aro de uniformaj pluredroj, Phil. Trans. 278 A (1975) pp. 111-135.
- M. Wenninger, Dualaj modeloj, CUP hbk (1983) ppbk (2003).
Eksteraj ligiloj
- Eric W. Weisstein, Vertica figuro en MathWorld.
- George Olshevsky, Vertica figuro en Glossary for Hyperspace.
- Verticaj figuroj
- Konsekvencaj verticaj priskriboj Arkivigite je 2007-02-20 per la retarkivo Wayback Machine