En geometrio, unuforma plurĉelo estas plurĉelo (aŭ 4-hiperpluredro) kiu estas unuforma hiperpluredro, do kiu estas vertico-transitiva kaj kies ĉeloj estas unuformaj pluredroj.
Ĉi tiu artikolo enhavas la plenan liston de 64 ne-prismaj konveksaj unuformaj plurĉeloj, kaj priskribas du malfiniajn arojn de konveksaj prismoj.
Historio de malkovro
- Regulaj hiperpluredroj: (konveksaj edroj)
- 1852: Ludwig Schläfli pruvis en sia manuskripto Theorie der vielfachen Kontinuität ke estas akurate 6 regulaj hiperpluredroj en 4 dimensioj kaj nur 3 en 5 aŭ pli multaj dimensioj.
- Regulaj stelaj plurĉeloj (kun stelaj pluredraj ĉeloj aŭ verticaj figuroj)
- 1852: Ludwig Schläfli ankaŭ trovis na 4 el la 10 regulaj stelaj plurĉeloj, nekonsiderinte tiujn 6 kun ĉeloj aŭ verticaj figuroj {5/2,5} kaj {5,5/2}.
- 1883: Edmund Hess plenigis la liston de 10 nekonveksaj regulaj plurĉeloj en sia libro Einleitung in die Lehre von der Kugelteilung mit besonderer Berücksichtigung ihrer Anwendung auf die Theorie der Gleichflächigen und der gleicheckigen Polyeder .
- Duonregulaj hiperpluredroj: (konveksaj)
- 1900: Thorold Gosset publikigis liston de neprismaj duonregulaj konveksaj hiperpluredroj kun regulaj ĉeloj (platonaj solidoj) en lia eldono Pri la regulaj kaj duoneregulaj figuroj en spaco de n dimensioj.
- 1912: E. L. Elte elvolvis la aferon surbaze de laboro de Gosset en eldono La duonregulaj hiperpluredroj de la hiperspacoj, inkluzivante specialan subaron de hiperpluredroj kun duonregulaj facetoj (tiuj konstrueblaj per sola ringita vertico de figuro de Coxeter-Dynkin.)
- Konveksaj unuformaj hiperpluredroj:
- 1910: Alicia Boole Stott, en ŝia eldono Geometria konkludo de duonregulaj surbaze de regulaj hiperpluredroj kaj spacaj plomboj elvolvis la difinon per permeso de ankaŭ arĥimedaj solidoj kaj prismaj ĉeloj.
- 1940: La serĉo estis elvolvita sisteme de Harold Scott MacDonald Coxeter en lia eldono Regulaj kaj duonregulaj hiperpluredroj.
- Konveksaj unuformaj plurĉeloj:
- 1965: La plena listo de konveksaj formoj estis farita de John Horton Conway kaj Michael Guy en ilia eldono Kvar-dimensiaj arĥimedaj hiperpluredroj. La laboro estas farita per komputila serĉado. Estis trovita nur unu konveksa plurĉelo kiu ne povas esti konstruita per konstruo de Wythoff - la spacograndigita kontraŭprismo.
- 1997: Plena numerado de la nomoj kaj eroj de la konveksaj unuformaj plurĉeloj estas donita surlinie de George Olshevsky.
- 2004: Pruvo ke la aro de Conway kaj'Guy estas plena estis publikigita de Marco Möller en lia disertaĵo Vierdimensionale Archimedische Polytope.
- Neregulaj unuformaj stelaj plurĉeloj (nekonveksaj):
- Daŭriĝas: Miloj de nekonveksaj unuformaj plurĉeloj estas sciataj, sed plejparte ili estas nepublikigitaj. La listo estas supozita al ne esti plena, kaj ne estas sciate kiam la plena listo estos farita.
Regulaj plurĉeloj
La unuformaj plurĉeloj inkluzivas 16 regulajn plurĉelojn:
- 6 konveksaj regulaj plurĉeloj
- 10 nekonveksaj plurĉeloj de Schläfli-Hess
Ĉi el la 16 havas propraĵo ke ĉiuj ĉeloj, edroj, lateroj, kaj verticoj estas kongruaj.
Konveksaj unuformaj plurĉeloj
Estas 64 konveksaj unuformaj plurĉeloj, inkluzivanta la 6 konveksajn regulajn plurĉelojn, kaj malinkluzivante la malfiniajn arojn de la duprismoj kaj la kontraŭprismaj hiperprismoj.
- 5 estas pluredraj prismoj bazita sur la platonaj solidoj .El ili 1 interkovras kun la regulaj ĉar la unuforma kuba hiperprismo estas regula 4-hiperkubo; do 4 la novaj formoj.
- 13 estas pluredraj prismoj bazita sur la arĥimedaj solidoj
- 9 estas en la mem-duala regula {3,3,3} (5-ĉelo) familio.
- 9 estas en la mem-duala regula {3,4,3} (24-ĉelo) familio (malinkluzivante riproĉan 24-ĉelon).
- 15 estas en la regula {3,3,4} (4-hiperkubo/16-ĉelo) familio El ili 3 interkovras kun 24-ĉela familio; do 12 la novaj formoj.
- 15 estas en la regula {3,3,5} (120-ĉelo/600-ĉelo) familio.
- 1 speciala riproĉa formo en la {3,4,3} (24-ĉelo) familio - la riproĉa 24-ĉelo.
- 1 speciala kiu ne povas esti konstruita per konstruo de Wythoff - la spacograndigita kontraŭprismo.
- Entute: 4+13+9+9+12+15+1+1=64
Aldone al la 64 pli supre listigitaj, estas 2 malfiniaj prismaj aroj kiuj generas ĉiujn la ceterajn konveksajn formojn:
- Aro de unuformaj kontraŭprismaj prismoj - s{p,2}x{} - ĉiu el ili estas 4-dimensia prismo kun konveksa kontraŭprismo kiel la bazo.
- Aro de unuformaj duprismoj - {p}x{q} - ĉiu el ili estas kartezia produto de du konveksaj plurlateroj.
A4 {3,3,3} (5-ĉela) familio
La bildoj estas desegnitaj kiel projekcioj de figuroj de Schlegel centritaj je la ĉelo de situo 3, kun konsekvenca orientiĝo, kaj la 5 ĉeloj je situo 0 estas montritaj solide.
| Nomo | Bildo | Figuro de Coxeter-Dynkin kaj simbolo de Schläfli |
Ĉeloj laŭ situo | Ĉeloj | Edroj | Lateroj | Verticoj | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Situo 3 (5) |
Situo 2 (10) |
Situo 1 (10) |
Situo 0 (5) | |||||||
| 5-ĉelo | {3,3,3} |
(3.3.3) |
5 | 10 | 10 | 5 | ||||
| Senpintigita 5-ĉelo | t0,1{3,3,3} |
(3.6.6) |
(3.3.3) |
10 | 30 | 40 | 20 | |||
| Rektigita 5-ĉelo |  |
t1{3,3,3} |
(3.3.3.3) |
(3.3.3) |
10 | 30 | 30 | 10 | ||
| Laterotranĉita 5-ĉelo |  |
t0,2{3,3,3} |
(3.4.3.4) |
(3.4.4) |
(3.3.3.3) |
20 | 80 | 90 | 30 | |
| Rektigitotranĉita 5-ĉelo |  |
t0,1,2{3,3,3} |
(4.6.6) |
(3.4.4) |
(3.6.6) |
20 | 80 | 120 | 60 | |
| Edroverticotranĉita 5-ĉelo |  |
t0,1,3{3,3,3} |
(3.6.6) |
(4.4.6) |
(3.4.4) |
(3.4.3.4) |
30 | 120 | 150 | 60 |
| *Dutranĉita 5-ĉelo |  |
t1,2{3,3,3} |
(3.6.6) |
(3.6.6) |
10 | 40 | 60 | 30 | ||
| *Edrotranĉita 5-ĉelo |  |
t0,3{3,3,3} |
(3.3.3) |
(3.4.4) |
(3.4.4) |
(3.3.3) |
30 | 70 | 60 | 20 |
| *Entutotranĉita 5-ĉelo |  |
t0,1,2,3{3,3,3} |
(4.6.6) |
(4.4.6) |
(4.4.6) |
(4.6.6) |
30 | 150 | 240 | 120 |
La 5-ĉelo havas simplan kvinĉelan simetrion de ordo 120, izomorfia al la permutoj de kvin eroj, ĉar ĉiuj paroj de verticoj estas rilatantaj en la sama maniero.
*La tri formoj markitaj per asterisko havas la pli altan etenditan kvinĉelan simetrion, de ordo 240, ĉar ĉiu ero respektiva al ero de la fonta 5-ĉelo povas esti interŝanĝita kun ĉiu el la eroj respektivaj al eroj de la duala 5-ĉelo.
La C4 {4,3,3}/{3,3,4} (4-hiperkuba/16-ĉela) familio
4-hiperkuba familio
La bildoj estas desegnitaj kiel projekcioj de figuroj de Schlegel centritaj je la ĉelo de situo 3, kun konsekvenca orientiĝo, kaj la 16 ĉeloj je situo 0 estas montritaj solide alterne kolorigite.
| Nomo | Bildo | Figuro de Coxeter-Dynkin kaj simbolo de Schläfli |
Ĉeloj laŭ situo | Ĉeloj | Edroj | Lateroj | Verticoj | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Situo 3 (8) |
Situo 2 (24) |
Situo 1 (32) |
Situo 0 (16) | |||||||
| 4-hiperkubo (8-ĉelo) |
 |
{4,3,3} |
(4.4.4) |
8 | 24 | 32 | 16 | |||
| Senpintigita 4-hiperkubo |  |
t0,1{4,3,3} |
(3.8.8) |
(3.3.3) |
24 | 88 | 128 | 64 | ||
| Rektigita 4-hiperkubo | 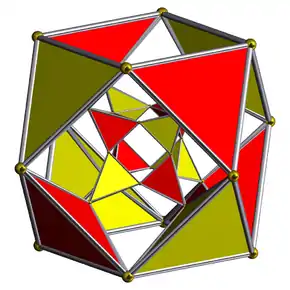 |
t1{4,3,3} |
(3.4.3.4) |
(3.3.3) |
24 | 88 | 96 | 32 | ||
| Laterotranĉita 4-hiperkubo | 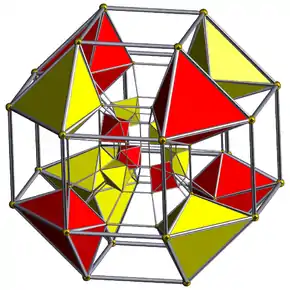 |
t0,2{4,3,3} |
(3.4.4.4) |
(3.4.4) |
(3.3.3.3) |
56 | 248 | 288 | 96 | |
| Rektigitotranĉita 4-hiperkubo |  |
t0,1,2{4,3,3} |
(4.6.8) |
(3.4.4) |
(3.6.6) |
56 | 248 | 384 | 192 | |
| Edroverticotranĉita 4-hiperkubo |  |
t0,1,3{4,3,3} |
(3.8.8) |
(4.4.8) |
(3.4.4) |
(3.4.3.4) |
80 | 368 | 480 | 192 |
| Dutranĉita 4-hiperkubo (dutranĉita 16-ĉelo) |
 |
t1,2{4,3,3} |
(4.6.6) |
(3.6.6) |
24 | 120 | 192 | 96 | ||
| Edrotranĉita 4-hiperkubo (edrotranĉita 16-ĉelo) |
 |
t0,3{4,3,3} |
(4.4.4) |
(4.4.4) |
(3.4.4) |
(3.3.3) |
80 | 208 | 192 | 64 |
| Entutotranĉita 4-hiperkubo (entutotranĉita 16-ĉelo) |
 |
t0,1,2,3{3,3,4} |
(4.6.8) |
(4.4.8) |
(4.4.6) |
(4.6.6) |
80 | 464 | 768 | 384 |
16-ĉela familio
La bildoj estas desegnitaj kiel projekcioj de figuroj de Schlegel centritaj je la ĉelo de situo 0, kun konsekvenca orientiĝo, kaj la 8 ĉeloj je situo 3 estas montritaj solide, dukolore en du prismaj aroj.
| Nomo | Bildo | Figuro de Coxeter-Dynkin kaj simbolo de Schläfli |
Ĉeloj laŭ situo | Ĉeloj | Edroj | Lateroj | Verticoj | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Situo 3 (8) |
Situo 2 (24) |
Situo 1 (32) |
Situo 0 (16) | |||||||
| 16-ĉelo |  |
{3,3,4} |
(3.3.3) |
16 | 32 | 24 | 8 | |||
| Senpintigita 16-ĉelo |  |
t0,1{3,3,4} |
(3.3.3.3) |
(3.6.6) |
24 | 96 | 120 | 48 | ||
| *Rektigita 16-ĉelo (24-ĉelo) |
 |
t1{3,3,4} |
(3.3.3.3) |
(3.3.3.3) |
24 | 96 | 96 | 24 | ||
| *Laterotranĉita 16-ĉelo (rektigita 24-ĉelo) |
 |
t0,2{3,3,4} |
(3.4.3.4) |
(4.4.4) |
(3.4.3.4) |
48 | 240 | 288 | 96 | |
| *Rektigitotranĉita 16-ĉelo (senpintigita 24-ĉelo) |
 |
t0,1,2{3,3,4} |
(4.6.6) |
(4.4.4) |
(4.6.6) |
48 | 240 | 384 | 192 | |
| Edroverticotranĉita 16-ĉelo |  |
t0,1,3{3,3,4} |
(3.4.4.4) |
(4.4.4) |
(4.4.6) |
(3.6.6) |
80 | 368 | 480 | 192 |
| Dutranĉita 16-ĉelo (dutranĉita 4-hiperkubo) |
 |
t1,2{3,3,4} |
(4.6.6) |
(3.6.6) |
24 | 120 | 192 | 96 | ||
| Edrotranĉita 16-ĉelo (edrotranĉita 4-hiperkubo) |
 |
t0,3{3,3,4} |
(4.4.4) |
(4.4.4) |
(3.4.4) |
(3.3.3) |
80 | 208 | 192 | 64 |
| Entutotranĉita 16-ĉelo (entutotranĉita 4-hiperkubo) |
 |
t0,1,2,3{3,3,4} |
(4.6.8) |
(4.4.8) |
(4.4.6) |
(4.6.6) |
80 | 464 | 768 | 384 |
Ĉi tiu familio havas simplan 16-ĉelan simetrion, de ordo 24*16=384: 4!=24 permutoj de la kvar hakoj, 24=16 por reflektoj laŭ ĉiu akso.
(*) Simile al tio kiel rektigo de la kvaredro produktas la okedron, rektigo de la 16-ĉelo produktas la 24-ĉelon, la regula membron de ĉi tiu familio. Markitaj per "*" plurĉeloj havas simplan 24-ĉelan simetrion de ordo 1152, vidu pli detale en la sekva ĉapitro.
La F4 {3,4,3} (24-ĉela) familio
| Nomo | Bildo | Figuro de Coxeter-Dynkin kaj simbolo de Schläfli |
Ĉeloj laŭ situo | Ĉeloj | Edroj | Lateroj | Verticoj | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Situo 3 (24) |
Situo 2 (96) |
Situo 1 (96) |
Situo 0 (24) | |||||||
| 24-ĉelo (rektigita 16-ĉelo) |
 |
{3,4,3} |
(3.3.3.3) |
24 | 96 | 96 | 24 | |||
| Senpintigita 24-ĉelo (rektigitotranĉita 16-ĉelo) |
 |
t0,1{3,4,3} |
(4.6.6) |
(4.4.4) |
48 | 240 | 384 | 192 | ||
| Rektigita 24-ĉelo (laterotranĉita 16-ĉelo) |
 |
t1{3,4,3} |
(3.4.3.4) |
(4.4.4) |
48 | 240 | 288 | 96 | ||
| Laterotranĉita 24-ĉelo |  |
t0,2{3,4,3} |
(3.4.4.4) |
(3.4.4) |
(3.4.3.4) |
144 | 720 | 864 | 288 | |
| Rektigitotranĉita 24-ĉelo | 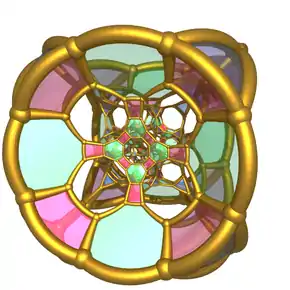 |
t0,1,2{3,4,3} |
(4.6.8) |
(3.4.4) |
(3.8.8) |
144 | 720 | 1152 | 576 | |
| Edroverticotranĉita 24-ĉelo |  |
t0,1,3{3,4,3} |
(4.6.6) |
(4.4.6) |
(3.4.4) |
(3.4.4.4) |
240 | 1104 | 1440 | 576 |
| *Dutranĉita 24-ĉelo | t1,2{3,4,3} |
(3.8.8) |
(3.8.8) |
48 | 336 | 576 | 288 | |||
| *Edrotranĉita 24-ĉelo |  |
t0,3{3,4,3} |
(3.3.3.3) |
(3.4.4) |
(3.4.4) |
(3.3.3.3) |
240 | 672 | 576 | 144 |
| *Entutotranĉita 24-ĉelo |  |
t0,1,2,3{3,4,3} |
(4.6.8) |
(4.4.6) |
(4.4.6) |
(4.6.8) |
240 | 1392 | 2304 | 1152 |
| **Riproĉa 24-ĉelo (alternita senpintigita 24-ĉelo) |
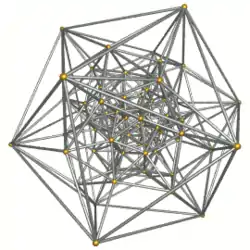 |
h0,1{3,4,3} |
(3.3.3.3.3) |
(3.3.3) (oblikva) |
(3.3.3) |
144 | 480 | 432 | 96 | |
Ĉi tiu familio havas simplan 24-ĉelan simetrion, de ordo 24*48=1152: la 48 simetrioj de la okedro por ĉiu el la 24 ĉeloj.
*La tri formoj markitaj per asterisko havas la pli altan etenditan 24-ĉelan simetrion, de duoble pli granda ordo 2304, ĉar ĉiu ero respektiva al ero de la fonta 24-ĉelo povas esti interŝanĝita kun ĉiu el la eroj respektivaj al eroj de la duala 24-ĉelo.
**La riproĉa 24-ĉelo ĉi tie, malgraŭ ĝia komuna nomo, ne estas analoga al la riproĉa kubo. Ĝi estas farata per alternado de la senpintigita 24-ĉelo. Ĝia simetria ordo estas nur 576 (la jona malkreskigita 24-ĉela grupo).
La G4 {5,3,3}/{3,3,5} (120-ĉela/600-ĉela) familio
| Nomo | Bildo | Figuro de Coxeter-Dynkin kaj simbolo de Schläfli |
Ĉeloj laŭ situo | Ĉeloj | Edroj | Lateroj | Verticoj | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Situo 3 (120) |
Situo 2 (720) |
Situo 1 (1200) |
Situo 0 (600) | |||||||
| 120-ĉelo |  |
{5,3,3} |
(5.5.5) |
120 | 720 | 1200 | 600 | |||
| 600-ĉelo |  |
{3,3,5} |
(3.3.3) |
600 | 1200 | 720 | 120 | |||
| Senpintigita 120-ĉelo |  |
t0,1{5,3,3} |
(3.10.10) |
(3.3.3) |
720 | 3120 | 4800 | 2400 | ||
| Senpintigita 600-ĉelo | t0,1{3,3,5} |
(3.3.3.3.3) |
(3.6.6) |
720 | 3600 | 4320 | 1440 | |||
| Rektigita 120-ĉelo |  |
t1{5,3,3} |
(3.5.3.5) |
(3.3.3) |
720 | 3120 | 3600 | 1200 | ||
| Rektigita 600-ĉelo |  |
t1{3,3,5} |
(3.3.3.3.3) |
(3.3.3.3) |
720 | 3600 | 3600 | 720 | ||
| Laterotranĉita 120-ĉelo |  |
t0,2{5,3,3} |
(3.4.5.4) |
(3.4.4) |
(3.3.3.3) |
1920 | 9120 | 10800 | 3600 | |
| Laterotranĉita 600-ĉelo |  |
t0,2{3,3,5} |
(3.5.3.5) |
(4.4.5) |
(3.4.3.4) |
1440 | 8640 | 10800 | 3600 | |
| Rektigitotranĉita 120-ĉelo |  |
t0,1,2{5,3,3} |
(4.6.10) |
(3.4.4) |
(3.6.6) |
1920 | 9120 | 14400 | 7200 | |
| Rektigitotranĉita 600-ĉelo |  |
t0,1,2{3,3,5} |
(5.6.6) |
(4.4.5) |
(4.6.6) |
1440 | 8640 | 14400 | 7200 | |
| Edroverticotranĉita 120-ĉelo |  |
t0,1,3{5,3,3} |
(3.10.10) |
(4.4.10) |
(3.4.4) |
(3.4.3.4) |
2640 | 13440 | 18000 | 7200 |
| Edroverticotranĉita 600-ĉelo |  |
t0,1,3{3,3,5} |
(3.4.5.4) |
(4.4.5) |
(4.4.6) |
(3.6.6) |
2640 | 13440 | 18000 | 7200 |
| Dutranĉita 120-ĉelo (dutranĉita 600-ĉelo) |
t1,2{5,3,3} |
(5.6.6) |
(3.6.6) |
720 | 4320 | 7200 | 3600 | |||
| Edrotranĉita 120-ĉelo (edrotranĉita 600-ĉelo) |
 |
t0,3{5,3,3} |
(5.5.5) |
(4.4.5) |
(3.4.4) |
(3.3.3) |
2640 | 7440 | 7200 | 2400 |
| Entutotranĉita 120-ĉelo (entutotranĉita 600-ĉelo) |
t0,1,2,3{5,3,3} |
(4.6.10) |
(4.4.10) |
(4.4.6) |
(4.6.6) |
2640 | 17040 | 28800 | 14400 | |
Ĉi tiu familio havas simplan 120-ĉelan simetrion, de ordo 120*120=24*600=14400: 120 por ĉiu el la 120 dekduedroj, aŭ 24 por ĉiu el la 600 kvaredroj.
La B4 [31,1,1] grupa familio
Ĉi tiu familio ne donas la novajn unuformajn plurĉelojn, sed indas ripeti ĉi tiujn alternativajn konstruojn.
| Nomo | Bildo | Figuro de Coxeter-Dynkin kaj simbolo de Schläfli |
Ĉeloj laŭ situo | Ĉeloj | Edroj | Lateroj | Verticoj | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Situo 0 (8) |
Situo 1 (24) |
Situo 0' (8) |
Situo 3 (8) |
Situo A (96) | |||||||
| 16-ĉelo |  |
t0{31,1,1} |
(3.3.3) |
(3.3.3) |
16 | 32 | 24 | 8 | |||
| Senpintigita 16-ĉelo |  |
t0,1{31,1,1} |
(3.3.3.3) |
(3.6.6) |
(3.6.6) |
24 | 96 | 120 | 48 | ||
| Rektigita 4-hiperkubo |  |
t0,2{31,1,1} |
(3.3.3) |
(3.3.3) |
(3.4.3.4) |
24 | 88 | 96 | 32 | ||
| Dutranĉita 4-hiperkubo |  |
t0,1,2{31,1,1} |
(3.6.6) |
(3.6.6) |
(4.6.6) |
24 | 120 | 192 | 96 | ||
| 24-ĉelo | t1{31,1,1} |
(3.3.3.3) |
(3.3.3.3) |
(3.3.3.3) |
24 | 96 | 96 | 24 | |||
| Rektigita 24-ĉelo |  |
t0,2,3{31,1,1} |
(3.4.3.4) |
(4.4.4) |
(3.4.3.4) |
(3.4.3.4) |
48 | 240 | 288 | 96 | |
| Senpintigita 24-ĉelo |  |
t0,1,2,3{31,1,1} |
(4.6.6) |
(4.4.4) |
(4.6.6) |
(4.6.6) |
48 | 240 | 384 | 192 | |
| Riproĉa 24-ĉelo |  |
s{31,1,1} |
(3.3.3.3.3) |
(3.3.3) |
(3.3.3.3.3) |
(3.3.3.3.3) |
(3.3.3) |
144 | 480 | 432 | 96 |
Ĉi tie denove la riproĉa 24-ĉelo prezentas alternadon de la senpintigita 24-ĉelo, kreante 96 novajn kvaredrojn je la situoj de la forigataj verticoj. En kontrasto al ĝia aperoj en antaŭaj grupoj kiel parte riproĉigita plurĉelo, nur en ĉi tiu geometria simetria grupo ĝi havas la plenan analogecon al la 3-dimensiaj la riproĉa kubo kaj la riproĉa dekduedro.
La spacograndigita kontraŭprismo
Estas unu unuforma konveksa plurĉelo kiu ne povas esti konstruita per konstruo de Wythoff - la spacograndigita kontraŭprismo, konsistanta de 20 kvinlateraj kontraŭprismoj formantaj du perpendikularajn ringojn kunigitajn per 300 kvaredroj. Ĝi estas iel analoga al la tri-dimensiaj kontraŭprismoj, kiuj konsistas el du paralelaj plurlateroj kunigitaj per bando de trianguloj; sed malsimile al ili la spacograndigita kontraŭprismo ne estas membro de malfinia familio de unuformaj hiperpluredroj.
Ĝia simetria ordo estas 400 (la jona malkreskigita grupo).
| Nomo | Bildo | Figuro de Coxeter-Dynkin kaj simbolo de Schläfli |
Ĉeloj laŭ speco | Ĉeloj | Edroj | Lateroj | Verticoj | |
|---|---|---|---|---|---|---|---|---|
| Spacograndigita kontraŭprismo |  |
Ne ekzistas ne ekzistas |
300 (3.3.3) |
20 (3.3.3.5) |
320 | 20 {5} 700 {3} |
500 | 100 |
Prismaj unuformaj plurĉeloj
Estas tri malfiniaj familioj de unuformaj plurĉeloj kiuj estas konsiderataj kiel prismaj, en tiu senco ke ili ĝeneraligas la propraĵoj de la 3-dimensiaj prismoj. Prisma hiperpluredro estas kartezia produto de du hiperpluredroj de subaj dimensioj. Estas kvar manieroj ricevi 4-dimensian plurĉelon per kartezia produto:
- {p,q}x{} -




 - {p,q}-pluredra prismo
- {p,q}-pluredra prismo - {p}x{q} -




 - p-latera q-latera duprismo
- p-latera q-latera duprismo - {p}x{}x{} -





 - plurlateraj prismaj prismoj - (la samo kiel {p}x{4})
- plurlateraj prismaj prismoj - (la samo kiel {p}x{4}) - {}x{}x{}x{} -






 - 4-hiperkubo (ne malfinia serio)
- 4-hiperkubo (ne malfinia serio)
Pluredraj prismoj
Unu el familioj de prismaj plurĉeloj estas la pluredraj prismoj, ĉiu el kiuj estas kartezia produto de pluredro kun streko. La ĉeloj de ĉi tia plurĉelo estas du identaj unuformaj pluredroj situantaj en paralelaj hiperebenoj (la bazaj ĉeloj) kaj tavolo de prismoj kunigataj ilin (la flankaj ĉeloj). Ĉi tiu familio inkluzivas prismojn por la 75 neprismaj unuformaj pluredroj. El ili 18 estas konveksa, 5 kreitaj de platonaj solidoj kaj 13 kreitaj de arĥimedaj solidoj. Unu el ili tiuj, la kuba prismo, estas listigita pli supre kiel la 4-hiperkubo.
Ankaŭ ekzistas pluredraj prismoj surbaze de la malfiniaj familioj de tri-dimensiaj prismoj kaj kontraŭprismoj.
La simetria ordo de pluredra prismo estas dufoje de tiu de la baza pluredro, krom specialaj okazoj kiam bazaj kaj flankaj ĉeloj estas la samaj, tiam la ordo estas pli granda.
Kvaredraj prismoj: A3xA1 - {3,3}x{}
| Nomo | Bildo | Figuro de Coxeter-Dynkin kaj simbolo de Schläfli |
Ĉeloj laŭ speco | Ĉeloj | Edroj | Lateroj | Verticoj | ||
|---|---|---|---|---|---|---|---|---|---|
| Kvaredra prismo |  |
t0{3,3}x{} |
2 3.3.3 |
4 3.4.4 |
6 | 8 {3} 6 {4} |
16 | 8 | |
| Senpintigita kvaredra prismo |  |
t0,1{3,3}x{} |
2 3.6.6 |
4 3.4.4 |
4 4.4.6 |
10 | 8 (3) 8 {4} 8 {6} |
48 | 24 |
| Rektigita kvaredra prismo (okedra prismo) |
 |
t1{3,3}x{} |
2 3.3.3.3 |
4 3.4.4 |
6 | 16 {3} 12 {4} |
30 | 12 | |
| Laterotranĉita kvaredra prismo (kubokedra prismo) |
 |
t0,2{3,3}x{} |
2 3.4.3.4 |
8 3.4.4 |
6 4.4.4 |
16 | 16 {3} 36 {4} |
60 | 24 |
| Rektigitotranĉita kvaredra prismo (senpintigita okedra prismo) |
 |
t0,1,2{3,3}x{} |
2 4.6.6 |
8 3.4.4 |
6 4.4.4 |
16 | 48 {4} 16 {6} |
96 | 48 |
| Riproĉa kvaredra prismo (dudekedra prismo) |
 |
s{3,3}x{} |
2 3.3.3.3.3 |
20 3.4.4 |
22 | 40 {3} 30 {4} |
72 | 24 | |
Okedraj prismoj: C3xA1 - {4,3}x{}
| Nomo | Bildo | Figuro de Coxeter-Dynkin kaj simbolo de Schläfli |
Ĉeloj laŭ speco | Ĉeloj | Edroj | Lateroj | Verticoj | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Kuba prismo (4-hiperkubo) (4-4 duprismo) |
 |
t0{4,3}x{} |
2 4.4.4 |
6 4.4.4 |
8 | 24 {4} | 32 | 16 | ||
| Okedra prismo (rektigita kvaredra prismo) (kvadrata kontraŭprisma prismo) |
 |
t2{4,3}x{} |
2 3.3.3.3 |
8 3.4.4 |
10 | 16 {3} 12 {4} |
30 | 12 | ||
| Kubokedra prismo (laterotranĉita kvaredra prismo) |
 |
t1{4,3}x{} |
2 3.4.3.4 |
8 3.4.4 |
6 4.4.4 |
16 | 16 {3} 36 {4} |
60 | 24 | |
| Senpintigita kuba prismo | 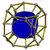 |
t0,1{4,3}x{} |
2 3.8.8 |
8 3.4.4 |
6 4.4.8 |
16 | 16 {3} 36 {4} 12 {8} |
96 | 48 | |
| Senpintigita okedra prismo (rektigitotranĉita kvaredra prismo) |
 |
t1,2{4,3}x{} |
2 4.6.6 |
6 4.4.4 |
8 4.4.6 |
16 | 48 {4} 16 {6} |
96 | 48 | |
| Rombokub-okedra prismo |  |
t0,2{4,3}x{} |
2 3.4.4.4 |
8 3.4.4 |
18 4.4.4 |
28 | 16 {3} 84 {4} |
120 | 96 | |
| Senpintigita kubokedra prismo |  |
t0,1,2{4,3}x{} |
2 4.6.8 |
12 4.4.4 |
8 4.4.6 |
6 4.4.8 |
28 | 96 {4} 16 {6} 12 {8} |
192 | 96 |
| Riproĉa kuba prismo |  |
s{4,3}x{} |
2 3.3.3.3.4 |
32 3.4.4 |
6 4.4.4 |
40 | 64 {3} 72 {4} |
144 | 48 | |
Dudekedraj prismoj: G3xA1 - {5,3}x{}
| Nomo | Bildo | Figuro de Coxeter-Dynkin kaj simbolo de Schläfli |
Ĉeloj laŭ speco | Ĉeloj | Edroj | Lateroj | Verticoj | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Dekduedra prismo |  |
t0{5,3}x{} |
2 5.5.5 |
12 4.4.5 |
14 | 30 {4} 24 {5} |
80 | 40 | ||
| Dudekedra prismo (riproĉa kvaredra prismo) |
 |
t2{5,3}x{} |
2 3.3.3.3.3 |
20 3.4.4 |
22 | 40 {3} 30 {4} |
72 | 24 | ||
| Dudek-dekduedra prismo |  |
t1{5,3}x{} |
2 3.5.3.5 |
20 3.4.4 |
12 4.4.5 |
34 | 40 {3} 60 {4} 24 {5} |
150 | 60 | |
| Senpintigita dekduedra prismo |  |
t0,1{5,3}x{} |
2 3.10.10 |
20 3.4.4 |
12 4.4.5 |
34 | 40 {3} 90 {4} 24 {10} |
240 | 120 | |
| Senpintigita dudekedra prismo |  |
t1,2{5,3}x{} |
2 5.6.6 |
12 4.4.5 |
20 4.4.6 |
34 | 90 {4} 24 {5} 40 {6} |
240 | 120 | |
| Rombo-dudek-dekduedra prismo |  |
t0,2{5,3}x{} |
2 3.4.5.4 |
20 3.4.4 |
30 4.4.4 |
12 4.4.5 |
64 | 40 {3} 180 {4} 24 {5} |
300 | 120 |
| Senpintigita dudek-dekduedra prismo |  |
t0,1,2{5,3}x{} |
2 4.6.4.10 |
30 4.4.4 |
20 4.4.6 |
12 4.4.10 |
64 | 240 {4} 40 {6} 24 {5} |
480 | 240 |
| Riproĉa dekduedra prismo |  |
s{5,3}x{} |
2 3.3.3.3.5 |
80 3.4.4 |
12 4.4.5 |
94 | 240 {4} 40 {6} 24 {10} |
360 | 120 | |
Duprismoj D2pxD2q - {p}x{q}
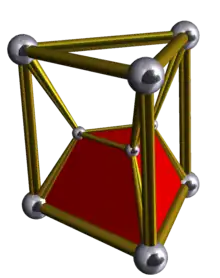
Ekzistas la malfinia familio de konveksaj unuformaj duprismoj, ĉiu el kiuj estas produtoj de du regulaj plurlateroj.
Ĉiu el ili havas figuron de Coxeter-Dynkin: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ĉi tiu familio interkovras kun la unua: se unu el la du faktoraj plurlateroj estas kvadrato, la produto estas ekvivalento al hiperprismo kies bazo estas tri-dimensia prismo. La 4-hiperkubo povas ankaŭ estas 4,4-duprismo.
La simetria ordo de duprismo kies faktoroj estas p-latero kaj q-latero ("p,q-duprismo") estas 4pq se p≠q; se la faktoroj estas ambaŭ p-lateroj la simetria ordo estas 8p2.
La eroj de p,q-duprismo (p ≥ 3, q ≥ 3) estas:
- Ĉeloj: p q-lateraj prismoj, q p-lateraj prismoj
- Edroj: pq kvadratoj, p q-lateroj, q p-lateroj
- Lateroj: 2pq
- Verticoj: pq
| 3,3 duprismo | 6 triangulaj prismoj | |
| 3,4 duprismo | 3 kuboj, 4 triangulaj prismoj | |
| 3,5 duprismo | 3 kvinlateraj prismoj, 5 triangulaj prismoj | |
| 3,6 duprismo | 3 seslateraj prismoj, 6 triangulaj prismoj | |
| 4,4 duprismo | 8 kuboj (la sama kiel 4-hiperkubo) | |
| 4,5 duprismo | 4 kvinlateraj prismoj, 5 kuboj | |
| 4,6 duprismo | 4 seslateraj prismoj, 6 kuboj | |
| 5,5 duprismo | 10 kvinlateraj prismoj | |
| 5,6 duprismo | 5 seslateraj prismoj, 6 kvinlateraj prismoj | |
| 6,6 duprismo | 12 seslateraj prismoj | |
| ... | ... | ... |
Estas ne unuforma analogo en kvar dimensioj al la malfinia familio de tri-dimensiaj kontraŭprismoj.
Plurlateraj prismaj prismoj: D2pxA1xA1 - {p}x{}x{}
La malfinia aro de konveksaj unuforma prismaj prismoj interkovras kun la 4,p duprismoj (p≥3):
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ĉiu enhavas p kubojn kaj 4 p-laterajn prismojn kaj estas la sama kiel 4-p duprismo.
- Triangula prisma prismo - la sama kiel 3-4 duprismo
- Kvadrata prisma prismo - la sama kiel 4-4 duprismo kaj kiel 4-hiperkubo
- Kvinlatera prisma prismo - la sama kiel 4-5 duprismo
- Seslatera prisma prismo - la sama kiel 4-6 duprismo
- Seplatera prisma prismo - la sama kiel 4-7 duprismo
- Oklatera prisma prismo - la sama kiel 4-8 duprismo
- ...
Plurlateraj kontraŭprismaj prismoj: DpdxA1 - (3.3.3.p) x {}
Ĉiu el la malfinia aroj de konveksaj unuformaj kontraŭprismaj prismoj estas konstruita de du paralelaj unuformaj kontraŭprismoj): (p≥3) - ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Ĝi enhavas 2 p-lateraj kontraŭprismoj, koneksajn per 2 p-lateraj prismoj kaj 2p triangulaj prismoj.
| Nomo | Figuro de Coxeter-Dynkin | Ĉeloj |
|---|---|---|
| Triangula kontraŭprisma prismo (okedra prismo) | 2 okedroj koneksaj per 8 triangulaj prismoj | |
| Kvadrata kontraŭprisma prismo | 2 kvadrataj kontraŭprismoj koneksaj per 2 kuboj kaj 8 triangulaj prismoj | |
| Kvinlatera kontraŭprisma prismo | 2 kvinlateraj kontraŭprismoj koneksaj per 2 kvinlateraj prismoj kaj 10 triangulaj prismoj | |
| Seslatera kontraŭprisma prismo | 2 seslateraj kontraŭprismoj koneksaj per 2 seslateraj prismoj kaj 12 triangulaj prismoj | |
| Seplatera kontraŭprisma prismo | 2 seplateraj kontraŭprismoj koneksaj per 2 seplateraj prismoj kaj 14 triangulaj prismoj | |
| Oklatera kontraŭprisma prismo | 2 oklateraj kontraŭprismoj koneksaj per 2 oklateraj prismoj kaj 16 triangulaj prismoj | |
| ... | ... | ... |
p-latera kontraŭprisma prismo havas 4p triangulajn, 4p kvadratajn kaj 4 p-laterajn edroj. Ĝi havas 10p laterojn, kaj 4p verticojn.
Geometriaj derivaĵoj por plurĉeloj
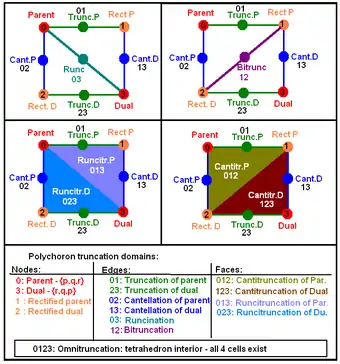

La 46 konveksaj unuformaj plurĉeloj, konstrueblaj per konstruo de Wythoff, inkluzivas la 6 konveksajn regulajn plurĉelojn. La aliaj 40 povas esti derivitaj de la regulaj plurĉeloj per geometriaj operacioj kiu konservas plejparton aŭ ĉiujn de iliaj simetrioj. Pro tio la plurĉeloj povas esti klasifikitaj per iliajla geometriaj simetriaj grupoj.
La geometriaj operacioj, kiuj derivas la 40 unuformajn plurĉelojn de la regulaj plurĉeloj, estas tranĉaj operacioj. De plurĉelo povas esti fortranĉitaj la verticoj, lateroj aŭ edroj, donante aldonajn ĉelojn respektivajn al tiuj eroj.
La figuro de Coxeter-Dynkin montras la kvar spegulojn de la kalejdoskopa konstruo de Wythoff, kiel verticojn, kaj la lateroj inter la verticoj estas markitaj per entjeroj montrantaj la angulon inter la speguloj. La angulo estas 180/n gradoj por latero markita kiel n. Ringigitaj verticoj montras, kiuj speguloj estas aktivaj por la formo. Tio, ke spegulo estas aktiva, signifas, ke la genera punkto situas for de la spegulo.
| Operacio | Simbolo de Schläfli | Figuro de Coxeter-Dynkin | Priskribo |
|---|---|---|---|
| Gepatro | t0{p,q,r} | Originala regula formo {p,q,r} | |
| Rektigo | t1{p,q,r} | Tranĉa operacio estas aplikita al verticoj ĝis la originalaj lateroj estas degeneritaj en punktojn. | |
| Durektigo | t2{p,q,r} | Tranĉa operacio estas aplikita al verticoj ĝis la originalaj edroj estas degeneritaj en punktojn. Sama kiel rektigita duala. | |
| Trirektigo (duala) |
t3{p,q,r} | Tranĉa operacio estas aplikita al verticoj ĝis la originalaj ĉeloj estas degeneritaj en punktojn. Sama kiel regula duala {r,q,p} | |
| Tranĉo | t0,1{p,q,r} | Ĉiu vertico estas dehakita tiel ke la mezo de ĉiu originala latero restas. Kie la vertico estis, tie aperas nova ĉelo, kun formo kiel la gepatra vertica figuro. Ĉiu originala ĉelo estas senpintigita. | |
| Dutranĉo | t1,2{p,q,r} | Tranĉo inter rektigita formo kaj la duala rektigita formo. | |
| Tritranĉo | t2,3{p,q,r} | Senpintigita duala {r,q,p} | |
| Laterotranĉo | t0,2{p,q,r} | Tranĉo estas aplikita al lateroj. Ankaŭ verticoj estas tranĉataj, sed nur ĝis minimuma ebla profundo. La rezulto estas inter la regula kaj duala rektigita formoj. | |
| Dulaterotranĉo | t1,3{p,q,r} | Laterotranĉita duala {r,q,p} | |
| Edrotranĉo (ekspansio, elvolvaĵo) |
t0,3{p,q,r} | Tranĉo estas aplikita al edroj. Ankaŭ verticoj kaj lateroj estas tranĉataj, sed nur ĝis minimuma ebla profundo. La rezulto estas inter regula (formo, formi) kaj la duala. | |
| Rektigitotranĉo | t0,1,2{p,q,r} | Ambaŭ la laterotranĉa kaj tranĉa operacioj estas aplikitaj kune. | |
| Durektigitotranĉo | t1,2,3{p,q,r} | Rektigitotranĉita duala {r,q,p} | |
| Edroverticotranĉo | t0,1,3{p,q,r} | Tranĉo estas aplikita al edroj. La verticoj de la fonta formo estas tranĉataj plu. Ankaŭ la lateroj estas tranĉataj, sed nur ĝis minimuma ebla profundo. Alivorte, ambaŭ la edrotranĉo kaj tranĉo operacioj estas aplikitaj kune. | |
| Edrolaterotranĉo | t0,1,3{p,q,r} | Tranĉo estas aplikita al edroj. La lateroj de la fonta formo estas tranĉataj plu. Ankaŭ la verticoj estas tranĉataj, sed nur ĝis minimuma ebla profundo. La samo kiel edroverticotranĉita duala {r,q,p} | |
| Entutotranĉo (edrolateroverticotranĉo) |
t0,1,2,3{p,q,r} | Tranĉo estas aplikita al edroj. La lateroj de la fonta formo estas tranĉataj plu. Poste la verticoj de la fonta formo estas tranĉataj plu. Havas ĉiujn tri operatorojn aplikitajn. |
Vidu ankaŭ pri konveksaj unuformaj ĉelaroj, iuj el kiuj ilustras ĉi tiuj operacioj kiel aplikitajn al la regula kuba kahelaro.
Se du hiperpluredroj estas dualaj unu al la alian (4-hiperkubo kaj 16-ĉelo; 120-ĉelo kaj 600-ĉelo), tiam dutranĉo, edrotranĉo kaj entutotranĉo produktas la samajn figurojn kiel rezultantajn se la sama operacio estas aplikita al al duala fonta plurĉelo.
Vidu ankaŭ
Referencoj
- Thorold Gosset, Pri la regulaj kaj duoneregulaj figuroj en spaco de n dimensioj, Kuriero de Matematiko, Macmillan, 1900
- Alicia Boole Stott, Geometria konkludo de duonregulaj surbaze de regulaj hiperpluredroj kaj spacaj plomboj, Verhandelingen of the Koninklijke academy van Wetenschappen width unit Amsterdam, Eerste Sectie 11,1, Amsterdamo, 1910
- E. L. Elte. (1912) La duonregulaj hiperpluredroj de la kiperspacoj. Groningen: Regna Universitato de Groningen. ISBN 141817968X.
- H. S. M. Coxeter, Regular Polytopes - Regulaj hiperpluredroj, 3-a. red., Dover Publications, 1973. ISBN 0-486-61480-8.
- Kalejdoskopoj: Elektitaj skriboj de H.S.M. Coxeter, redaktita de F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Papero 22) H.S.M. Coxeter, Regulaj kaj duonregulaj hiperpluredroj I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Papero 23) H.S.M. Coxeter, Regulaj kaj duonregulaj hiperpluredroj II, [Math. Zeit. 188 (1985) 559-591]
- (Papero 24) H.S.M. Coxeter, Regulaj kaj duonregulaj hiperpluredroj III, [Math. Zeit. 200 (1988) 3-45]
- John Horton Conway kaj Michael Guy: Kvar-dimensiaj arĥimedaj hiperpluredroj, Paperoj de la Kolokvo sur Konvekseco je Kopenhago, paĝo 38 kaj 39, 1965
- Norman Johnson: La teorio de unuformaj hiperpluredroj kaj kahelaroj, Ph.D. Disertaĵo, Universitato de Toronto, 1966
- Branko Grünbaum Konveksaj hiperpluredroj, Novjorko; Londono: Springer, c2003. ISBN 0-387-00424-6. Dua redakcio preparita de Volker Kaibel, Victor Klee, Günter M. Ziegler.
Eksteraj ligiloj
- Eric W. Weisstein, Unuforma plurĉelo en MathWorld.
- Stella4D Arkivigite je 2007-11-12 per la retarkivo Wayback Machine - programaro kiu produktas vidojn de unuformaj plurĉeloj.
Konveksaj unuformaj plurĉeloj
- Hiperpluredroj en R4 de Marco Möller
- 2004 Disertaĵo Arkivigite je 2005-03-22 per la retarkivo Wayback Machine
- Unuformaj hiperpluredroj en kvar dimensioj, George Olshevsky
- Regulaj kaj duonregulaj konveksaj hiperpluredroj - mallonga historia ĝenerala priskribo Arkivigite je 2003-08-18 per la retarkivo Wayback Machine
Nekonveksaj unuformaj plurĉeloj
- Unuformaj plurĉeloj de Jonathan Bowers