En geometrio, steligo estas unu el manieroj de konstruado de novaj plurlateroj en du dimensioj, novaj pluredroj en tri dimensioj, aŭ, ĝenerale, novaj hiperpluredroj en n dimensioj. La procezo konsistas de etendado de la eroj de rando de la fonta figuro (latero, edro, ...), kutime en simetria maniero, ĝis kiam ili renkontas unu la alian denove. La nova figuro estas steligo de la fonta.
Steligitaj plurlateroj
Steligo de regula plurlatero estas stelo, kiu povas esti plurlatero aŭ plurlatera kombinaĵo.
Ĝi povas esti prezentita per la simbolo {n/m}, kie n estas la kvanto de verticoj, kaj m estas la longo de paŝo uzata en la kunigo de verticoj. Se m estas unu, ĝi estas la nula steligo, la regula plurlatero {n}. Tiel la (m-1)-a steligo estas {n/m}.
Plurlatera kombinaĵo aperas, se n kaj m ne estas reciproke primaj (t.e se ili havas netrivialan komunan dividanton), kaj la plena steliga figuro postulas multajn ciklajn vojojn por plenumi ĝin. Ekzemple, {6/3} konsistas el 2 trianguloj {3}, kaj {10/4} konsistas el 2 stelokvinlateroj {5/2}.
Regula 'n-latero havas (n-4)/2 steligojn se n estas para, kaj (n-3)/2 steligojn se n estas nepara.
 La stelokvinlatero {5/2} estas la sola steligo de kvinlatero. |
 La {6/2}, la steligo de seslatero kaj kombinaĵo de du trianguloj. |
  La seplatero havas du steligojn, steloseplaterojn {7/2} kaj {7/3}. |
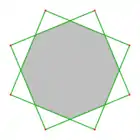 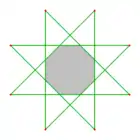 La oklatero havas du steligojn, stelooklaterojn {8/2}, {8/3}. La {8/2} estas kombinaĵo de du kvadratoj. |
 La naŭlatero havas 3 steligojn, stelonaŭlaterojn {9/2}, {9/3}, {9/4}, kie {9/3} estas kombinaĵo de 3 trianguloj. | |
Steligitaj pluredroj
 |
 |
 |
 |
 |
 |
 |
Edroj de pluredro dividas spaco en multajn diskretajn ĉelojn. Por simetria pluredro, ĉi tiuj ĉeloj estas en grupoj de kongruaj ĉeloj; oni povas diri ke la inter si kongruaj ĉeloj de ĉi tia grupo estas de la sama speco. Komuna maniero de trovado de steligoj engaĝas selekton de unu aŭ pli multaj ĉelaj specoj.
Ĉi tiu povas konduki al grandega kvanto de eblaj formoj, kaj oni ofte enkondukas pluajn kriteriojn por malpligrandigi la aron al ĉi tiuj steligoj.
Aro de ĉeloj formanta fermitan tavolon ĉirkaŭ ĝia kerno estas ŝelo. Por simetria pluredro, ŝelo povas esti farita el unu aŭ kelkaj ĉelaj specoj.
Tiel, kelkaj limigitaj kategorioj de steligoj estas identigitaj:
- Ĉefo-liniaj steligoj estas ricevataj per aldono de la sekvaj ŝeloj al la kerna pluredro.
- Plene subtenataj steligoj estas tiuj ĉe kiuj, kaj ĉiuj videblaj partoj de ĉiu edro estas vidataj de la sama flanko. Ne plene subtenataj steligoj povas havi formon similan al alero.
- Steligoj kun la sola speco de akraĵo estas tiu ĉe kiu estas nur unu speco de akraĵo, aŭ vertico, en steligo (kio estas ĉiuj verticoj estas kongrua en sola simetria orbito) (vidu ankaŭ en vertico-transitiva). Ĉiuj ĉi tiaj steligoj estas plene subtenataj.
- Unuecaj steligoj. Kie pluredro havas ebenojn de spegula simetrio, lateroj kuŝantaj en ĉi tiuj ebenoj estas dirataj al kuŝi en unuecaj linioj. Se ĉiuj lateroj kuŝas) en unuecaj linioj, la steligo estas unueca. Ĉiuj ĉi tiaj steligoj estas plene subtenataj.
- Steligoj de Miller. En libro "La Kvindek-Naŭ Dudekedroj" H.S.M. Coxeter, Du Val, Flather kaj Petrie skribas kvin regulojn sugestitajn de J.C.P. Miller. Kvankam ĉi tiuj reguloj temas aparte pri la regula dudekedro, ili povas facile esti adaptitaj al ajnaj pluredroj. Vidu detale pli sube. La kvar specoj de steligo supre difinitaj estas subaroj de la steligoj de Miller.
Oni povas ankaŭ identigi iujn aliajn kategoriojn:
- Parta steligo estas tiu ĉe kie ne ĉiuj eroj de donita dimensino estas etenditaj.
- Sub-simetria steligo estas tiu ĉe kie ne ĉiuj eroj estas etendita simetrie, kaj la rezultanta figuro do havas malpli grandan simetrion ol la fonta.
Ankaŭ arĥimedaj solidoj kaj ilia dualaj katalanaj solidoj povas esti steligitaj. Ĉi tie oni kutime aldonas la regulon ke ĉiuj el la originalaj edraj ebenoj devas ĉeesti en la steligo, kio estas ni ne konsideri partaj steligoj. Ekzemple la kubo estas ne konsiderita steligo de la kubokedro.
Laŭ iuj (???) donitaj supre reguloj, ekzistas:
- 4 steligoj de la romba dekduedro
- 187 steligoj de la trilateropiramidigita kvaredro
- 358,833,097 steligoj de la romba tridekedro
- 17 steligoj de la kubokedro (4 estas montritaj en listo de pluredroj de Wenninger)
- Nekonata kvanto de steligoj de la dudek-dekduedro, sed multe pli multaj ol la kvantoj donitaj pli supre! (19 estas montritaj en listo de pluredroj de Wenninger#Steligoj de dudek-dekduedro)
17 el la nekonveksaj unuformaj pluredroj estas steligoj de arĥimedaj solidoj.
Keplera difino
En 1619 Keplero difinis steligon por plurlateroj kaj pluredroj, kiel la procezo de etendo de lateroj aŭ edroj ĝis kiam ili kuniĝas por formi novan plurlateron aŭ pluredron. Li steligis la dekduedron kaj ricevis du el la regulaj stelaj pluredroj (du el la pluredroj de Keplero-Poinsot).
Reguloj de Miller
Reguloj de J.C.P. Miller por la regula dudekedro estas [1]:
- (1) La edroj devas kuŝi en 12 ebenoj de edroj de la regula dudekedro.
- (2) Ĉiuj partoj komponantaj la edrojn devas esti la samaj en ĉiu ebeno, kvankam ili povas esti malkoneksaj.
- (3) La partoj en ĉiu ebeno devas havi trioblan turnan simetrion, sen aŭ kun reflekta simetrio.
- (4) La partoj en ĉiu ebeno devas ĉiuj estas alireblaj en la plenumita solido de ekstere. Ĉi tio malpermesas enajn malplenaĵojn.
- (5) Estas malpermesataj okazoj kiam la partoj en la ebenoj povas esti dividitaj en du arojn, ĉiu aro donanta solidon de la sama simetrio kiel la tuta solido. Tamen estas permesataj kunaĵoj de du diversaj variantoj de nememspegula sub-solido, ne havantaj komunan parton. (Ĉi tio reale okazas en nur unu okazo). La regulo malebligas malkoneksajn kombinaĵojn de aliaj steligoj: La 59 dudekedroj konsideras vertico-koneksajn kaj latero-koneksaj samcentraj kombinaĵoj ne estas permesitaj, kvankam la regulo ŝajnas al esti ambigua.
Reguloj 1, 2, 3 garantias dudekedran simetrion de la solido.
Laŭ la reguloj, kaj laŭ la analogiaj reguloj por la aliaj fontaj pluredroj, rezultiĝas:
- Ne estas steligoj de la kvaredro, ĉar ĉiuj edroj estas najbaraj.
- Ne estas steligoj de la kubo, ĉar ne-najbaraj edroj estas paralelaj kaj tial ne povas esti etenditaj por fari novajn laterojn.
- Estas 1 steligo de la okedro, la stelookangulopluredro.
- Estas 3 steligoj de la dekduedro: la malgranda steligita dekduedro, la granda dekduedro kaj la granda steligita dekduedro, ili ĉiuj estas pluredroj de Keplero-Poinsot.
- Estas 58 steligoj de la dudekedro, inter ili la granda dudekedro (unu el la pluredroj de Keplero-Poinsot), kaj la 2-a kaj finaj steligoj de la dudekedro. La 59-a modelo en "La 59 Dudekedroj" estas la originala dudekedro mem.
Multaj steligoj de Miller ne povas esti ricevitaj rekte per uzo de la Keplera maniero. Ekzemple multaj havas kaldronajn centrojn kie la originalaj edroj kaj lateroj de la kerna pluredro tute forestas: estas nenio (maldekstre, restis) al esti steligita. Aliflanke, Keplera maniero ankaŭ donas steligojn kiu estas malpermesataj de reguloj de Miller pro tio ke iliaj ĉeloj estas latere aŭ vertice koneksaj, kvankam iliaj edroj estas solaj plurlateroj. Ĉi tiu malkoincido ne estis atentita ĝis Inchbald (2002).
Aliaj reguloj por steligo
Reguloj de Miller neniel donas la korektan manieron por numerigi la steligojn. Ili estas bazita sur komponigo de partoj en la steliga figuro en certaj vojoj, sed ne konsideras topologion de la rezultantaj edroj. Tiel iuj sufiĉe moderaj steligoj de la dudekedro ne estas steligoj de Miller; unu ĉi tiu estita identigita de James Bridge en 1974. Male iuj steligoj de Miller estas dubindaj rilate al tio ĉu ili devas esti estimita kiel steligoj ajn - unu el la dudekedra aro ampleksas kelkaj sufiĉe malkonektitaj ĉeloj flosanta simetrie en spaco.
Alternativa aro de reguloj ankoraŭ ne estas plene ellaborita. Plej granda progreso estas farita surbaze de tio ke steligo estas la inverso procezo de facetigo, kiu estas forpreno partoj de pluredro sen kreo de novaj verticoj. Por ĉiu steligo de iu pluredro, estas duala facetigo de la duala pluredro, kaj ree. Per studo de facetigoj de la duala pluredro, oni povas kompreni steligojn de la originala. James Bridge trovis sian novan steligon de la dudekedro per studo de la facetigoj de ĝia duala, la dekduedro.
Oni ankaŭ iam konsideras ke steligo estas du-voja procezo, tiel ke du pluredroj havantaj la samajn edraj ebenojn estas steligoj de unu la alia. Ĉi tio estas komprenebla se oni faras ĝeneralan algoritmon taŭgas por uzo en komputila programo, sed alie ne estas aparte helpema.
Nomoj de steligoj
La unua sistemo nomigo de steligitaj pluredroj estis sistemo de Cayley por la regulaj stelaj pluredroj. Ĉi tiu sistemo estis larĝe, sed ne ĉiam tute sistemece, adoptita por la aliaj pluredroj kaj pli alte dimensiaj hiperpluredroj.
John Horton Conway proponis terminaron por steligitaj plurlateroj, pluredroj kaj plurĉeloj. En ĉi tiu sistemo la procezo de etendo de lateroj por krei novan figuron estas nomata kiel steligo, procezo de etendo de edroj estas nomata kiel ebenograndigo kaj procezo de etendo de ĉeloj estas nomata kiel spacograndigo (ĉi tiu la lasta ne aplikiĝas al pluredroj, sed nur al plurĉeloj). Ĉi tio permesas sisteman uzo de vortoj steligita, ebenograndigita kaj spacograndigita en nomoj de la rezultantaj figuroj. Kun ĉi tio, Conway proponis iuj malgrandajn variadojn de la nomoj de la pluredroj de Keplero-Poinsot.
Vidu ankaŭ
- Listo de pluredroj de Wenninger inkluzivas 44 steligitajn formojn
- Artikolo pluredra kombinaĵo inkluzivas 5 regulajn kombinaĵojn kaj 4 dualajn regulajn kombinaĵojn.
Referencoj
Eksteraj ligiloj
- Eric W. Weisstein, Steligo en MathWorld.
- Steligado de dudekedro kaj facetado de dekduedro
- Numerado de steligoj
- Pluredra steligo de Vladimir Bulatov
- Steliga apleto
- Interaga kreado de pluredraj steligoj kun diversaj simetrioj
- La 59 dudekedroj - apleto Arkivigite je 2019-12-28 per la retarkivo Wayback Machine
- 59 steligoj de dudekedro de George Hart
- Steligo: bela matematiko Arkivigite je 2006-10-06 per la retarkivo Wayback Machine