Sistemo L aŭ Sistemo Lindenmayer estas formala gramatikaĵo (serio de reguloj kaj simboloj), kies plej konata uzo estas modeli la kreskon de plantoj, kaj duarange ankaŭ de fantaziaj kompleksaj geometriaj formoj. Tiajn sistemojn unuafoje evoluigis kaj prezentis dum la jaro 1968 la hungar-devena teoria biologo Arisztid Lindenmayer (1925–1989), en la Universitato de Utrecht en Nederlando.

Originoj

"trudherboj", generitaj de Sistemo L en tri dimensioj.

Kiel biologo, Lindenmayer laboris per gisto kaj filamentaj fungoj, kaj studis la kreskomekanismojn de multaj tipoj de algoj. Origine la Sistemoj L celis doni formalan priskribon de la kresko de tiaj multĉelaj organismoj, kaj de la najbaraj rilatoj de pluraj tiel kreskantaj plantoj. Pli poste, la sistemo plietendiĝis por priskribi ankaŭ pli ampleksajn plantojn kaj komplikajn branĉajn strukturojn.

La strukturo de Sistemo L

La reguloj de Sistemoj L rezultigas multajn strukturajn ripetojn kaj gvidas al fraktalaj formoj. Dum la kreskado la modelo plikompleksiĝas, kaj tial similiĝas al naturaj formoj. Modeloj de plantoj kaj nature aspektantaj organikaj formoj tiel surprize simple difiniĝas per matematika formala gramatikaĵo. La gramatikaĵo de la sistemoj de Aristid Lindenmayer cetere tre similas al la gramatikaĵo inventita de Noam Chomsky.

Sistemoj L difineblas per la formulo

G = {V, S, ω, P},

kie

  • V (la alfabeto) estas serio da simboloj, kiu enhavas elementojn anstataŭigeblajn ("varieblaĵoj")
  • S estas serio da simboloj, kiu enhavas elementojn fiksajn (konstantaĵoj)
  • ω (la startaĵo, iniciataĵo) estas vico da simboloj el la grupo V, kiu difinas la iniciatan staton de la sistemo.
  • P estas serio da reguloj, kiuj difinas la manieron, per kiuj iuj varieblaĵoj povas esti anstataŭigitaj per 'konstantaĵoj aŭ aliaj varieblaĵoj. "Produktaĵo" konsistas el du simbologrupoj, la antaŭaĵo kaj sekvaĵo.

Ekzemploj de Sistemoj L

Ekzemplo 1: Algoj

La origina Sistemo L de Lindenmayer celis modeli la kreskadon de algoj.

varieblaĵoj : A B
konstantaĵoj : neniuj
startaĵo : A
reguloj : (A → AB), (B → A)

- kio produktas la sekvon:

n = 0 : A
n = 1 : AB
n = 2 : ABA
n = 3 : ABAAB
n = 4 : ABAABABA

Ekzemplo 2: Fibonacci-numeroj

Se ni difinas la sekvan simplan gramatikaĵon

varieblaĵoj : A B
konstantaĵoj : neniuj
startaĵo : A
reguloj : (A → B), (B → AB)

tiam tiu Sistemo L produktas la sekvan simbolo-vicon

n = 0 : A
n = 1 : B
n = 2 : AB
n = 3 : BAB
n = 4 : ABBAB
n = 5 : BABABBAB
n = 6 : ABBABBABABBAB
n = 7 : BABABBABABBABBABABBAB

kaj se ni kalkulas la longecon de ĉiu simbolo-vico, ni ricevas la konatan Fibonacci-sekvon da numeroj:

1 1 2 3 5 8 13 21 34 55 89 ...

La sama Fibonacci-sekvo da numeroj rezultiĝas, se la regulo (B → AB) anstataŭiĝas per (B → BA).

Ekzemplo 3: nebulo de Cantor

varieblaĵoj : A B
konstantaĵoj : neniuj
startaĵo : A
reguloj : (A → ABA), (B → BBB)

En tio A signifas "pentru antaŭen" kaj B signifas "moviĝu antaŭen".

Produktiĝas la “nebulo de Cantor”.

Ekzemplo 4: neĝero de Koch

Jen variaĵo de la “neĝero de Koch“, kiu uzas nur rektangulojn:

varieblaĵoj : F
konstantaĵoj : + −
startaĵo : F
reguloj : (F → F+F−F−F+F)

Ĉi-tie, F signifas "pentru antaŭen", + signifas "turniĝu maldekstren je 90°", kaj - signifas "turniĝu dekstren je 90°".

n = 0: kvadrato de Koch - 0 paŝoj
F
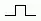
n = 1: kvadrato de Koch - 1 paŝo
F+F-F-F+F
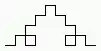
n = 2: kvadrato de Koch - 2 paŝoj
F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F
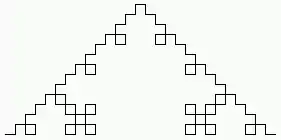
n = 3: kvadrato de Koch - 3 paŝoj
F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F+

F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F- F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F- F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F+

F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F

Ekzemplo 5: tegoloj de Penrose

La sekvaj bildoj estis generitaj fare de Sistemo L. Ili interrilatas kaj tre similas al la “tegoloj de Penrose”, kiujn enkondukis la scientisto Roger Penrose.

Ekzemplo 6: triangulo de Sierpinski

La “triangulo de Sierpinski”, desegnita pere de Sistemo L, aspektas jene:

varieblaĵoj : A B
konstantaĵoj : + −
startaĵo : A
reguloj : (A → B−A−B),(B → A+B+A)
angle : 60º

Ĉi-tie A kaj B ambaŭ signifas "pentru antaŭen", + signifas "turniĝu maldekstren je 60°", kaj - signifas "turniĝu dekstren je 60°". La turniĝo ŝanĝas sian direkton je ĉiu plena paŝo, tial ke la trianguloj ĉiam havas sian bazon malsupre (alikaze ili alterne estus supre kaj malsupre).

Evoluo por n = 2, n = 4, n = 6, n = 9

Ekzemplo 7: modifita figuro de Koch

Jen fine ankoraŭ fraktala figuro desegnita laŭ modifo de la baza “neĝero de Koch”:

Libro reta

Eksteraj ligiloj

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.