Malgranda rombokub-okedro
Pliaj nomoj Laterotranĉita kubo
Laterotranĉita okedro
Bildo
Bildo
Klaku por rigardi turnantan bildon
Vertica figuro 3.4.4.4
Bildo de vertico Bildo de vertico
Bildo de reto Bildo de reto
Simbolo de Wythoff 3 4 | 2
Simbolo de Schläfli
Figuro de Coxeter-Dynkin (o)4o3(o)
Indeksoj U10 C22 W13
Simbolo de Bowers Sirco
Verticoj 24
Lateroj 48
Edroj 26
Edroj detale 8{3}+(6+12){4}
χ 2
Geometria simetria grupo Oh
Duala Deltosimila dudekkvaredro
Bildo de duala 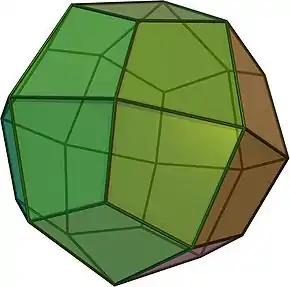Bildo de duala
La unua iam printita bildo de la rombokub-okedro de Leonardo da Vinci en la Divina Proportione

La rombokub-okedro aŭ malgranda rombokub-okedro aŭ laterotranĉita kubo aŭ laterotranĉita okedro estas pluredro, arkimeda solido kun 8 triangulaj kaj 18 kvadrataj edroj. Estas 24 identaj verticoj, kun unu triangulo kaj tri kvadratoj kuniĝantaj je ĉiu. 6 el 18 kvadratoj komunigas nur verticojn kun la trianguloj. La aliaj 12 kvadratoj komunigas laterojn kun la trianguloj. La pluredro havas okedran simetrion kiel kubo kaj okedro. Ĝia duala pluredro estas deltosimila dudekkvaredro aŭ trapeza dudekkvaredro, kvankam ĝiaj edroj ne estas veraj trapezoj.

La nomo rombokub-okedro referas al tiu fakto ke 12 el la kvadrataj edroj kuŝas en la samaj ebenoj kiel la 12 edroj de la romba dekduedro kiu estas duala al la kubokedro.

Ĝi estas ankaŭ laterotranĉita kubo aŭ laterotranĉita okedro kiel rezulto de laterotranĉaj operacioj de la regula kubo aŭ la regula okedro.

Areo kaj volumeno

La areo A kaj la volumeno V de la rombokub-okedro de randa longo a estas:

Karteziaj koordinatoj

Karteziaj koordinatoj de verticoj de rombokub-okedro centris je (0,0,0) kun latera longo 2 estas ĉiuj permutoj de

(±1, ±1, ±(1+√2))

Geometriaj rilatoj


Rombokub-okedro sekcita en du kvadratajn kupolojn kaj centra oklatera prismo. Turno de unu kupolo kreas la pseŭdo-rombokub-okedron.

Du formoj kun la sama vertica figuro: 3.4.4.4

Estas tri paroj de paralelaj ebenoj ĉiu el kiuj ebenoj sekcas la rombokub-okedron tra ok lateroj. La sekcaĵo havas formon de regula oklatero. Se distranĉi la rombokub-okedro samtempe per du ĉi tiaj paralelaj ebenoj do rezultiĝas oklatera prismo kun regulaj edroj kaj du kvadrataj kupoloj. La eroj povas esti rekunigitaj kun turno de unu kupolo je 45 gradoj kaj doni la alian pluredron - plilongigitan kvadratan turnodukupolon kiu havas simetrion de kvadrata kontraŭprismo. En ĉi tiu pluredro la verticoj estas ĉiuj loke la samaj kiel tiuj de rombokub-okedro, kun unu triangulo kaj tri kvadrata konferenco je ĉiu, sed ili ne estas identaj kun konsidero de la tuta pluredro.

La linioj laŭ kiu kubo de Rubik povas esti turnita estas topologie identaj, al la ebenoj de distranĉo de rombokub-okedro. Estadas, variantoj de la kubo de Rubik kun la sama ena mekanismo sed kun ekztero simila la rombokub-okedro.

La rombokub-okedro estas uzata en tri unuformaj spaco-enspacantaj kahelaroj: la laterotranĉita kuba ĉelaro, la edroverticotranĉita kuba ĉelaro kaj la edrotranĉita alternita kuba ĉelaro.`

La rombokub-okedro komunigas sian situon de verticoj kun tri stelaj unuformaj pluredroj: la steligita senpintigita sesedro, la malgranda rombo-sesedro kaj la malgranda kubokubo-okedro.


Steligita senpintigita sesedro
Malgranda rombo-sesedro
Malgranda kubokubo-okedro

En la artoj

La pluredro en la portreto de Luca Pacioli estas rombokub-okedra glaso duono-plenigita per akvo.

Vidu ankaŭ

Referencoj

  • Williams, Robert. (1979) The Geometrical Foundation of Natural Structure: A Source Book of Design - La Geometria Fundamento de Natura Strukturo: Fonta Libro de Dizajno. Dover Publications, Inc. ISBN 0-486-23729-X. (Sekcio 3-9)
  • Coxeter, H. S. M. (13-a de majo, 1954). “Uniform Polyhedra - Uniformaj Pluredroj”, Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences - Filozofiaj Transakcioj de la Reĝa Societo de Londono de Londono. Serio A, Matematikaj kaj Fizikaj Sciencoj 246, (916), p. 401–450.

Eksteraj ligiloj

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.