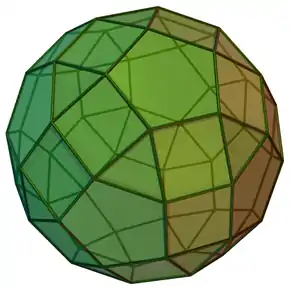
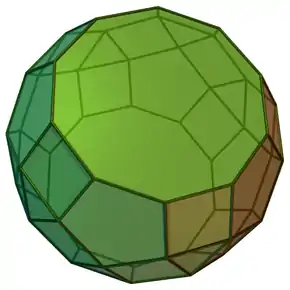
Malgranda rombo-dudek-dekduedro
Klaku por rigardi turnantan bildon
Vertica figuro	3.4.5.4
Bildo de vertico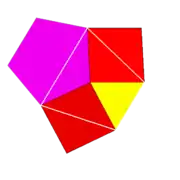
Bildo de reto
Simbolo de Wythoff	3 5 | 2
Simbolo de Schläfli	${\displaystyle r{\begin{Bmatrix}3\\5\end{Bmatrix}}}$
Figuro de Coxeter-Dynkin
Indeksoj	U27 C30 W14
Simbolo de Bowers	Srid
Verticoj	60
Lateroj	120
Edroj	62
Edroj detale	20{3}+30{4}+12{5}
χ	2
Geometria simetria grupo	Ih
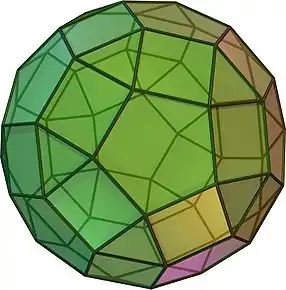
Duala	Deltosimila sesdekedro
Bildo de duala

La rombo-dudek-dekduedro aŭ malgranda rombo-dudek-dekduedro estas pluredro, arĥimeda solido. Ĝi havas 20 regulajn triangulajn edrojn, 30 regulajn kvadratajn edrojn, 12 regulajn kvinlaterajn edrojn, 60 verticojn kaj 120 laterojn.

La nomo rombo-dudek-dekduedro referas al la tiu fakto ke la 30 kvadrataj edroj kuŝas en la samaj ebenoj kiel 30 edroj de la romba tridekedro kiu estas duala al la dudek-dekduedro.

Ĝi povas esti nomata ankaŭ kiel laterotranĉita dekduedro aŭ laterotranĉita dudekedro de laterotranĉaj operacioj de ĉi tiuj du pluredroj.

Areo kaj volumeno

La areo A kaj la volumeno V de rombo-dudek-dekduedro de latera longo a estas:

${\displaystyle {\begin{aligned}A&=\left\{30+{\sqrt {30\left[10+3{\sqrt {5}}+{\sqrt {15(5+2{\sqrt {5}})}}\right]}}\right\}a^{2}\\&\approx 59.3059828a^{2}\\V&={\frac {1}{3}}(60+29{\sqrt {5}})a^{3}\approx 41.6153238a^{3}\\\end{aligned}}}$

Karteziaj koordinatoj

Karteziaj koordinatoj de verticoj de rombo-dudek-dekduedro centrita je (0, 0, 0) estas

(±1, ±1, ±τ³),

(±τ³, ±1, ±1),

(±1, ±τ³, ±1),

(±τ², ±τ, ±2τ),

(±2τ, ±τ², ±τ),

(±τ, ±2τ, ±τ²),

(±(2+τ), 0, ±τ²),

(±τ², ±(2+τ), 0),

(0, ±τ², ±(2+τ)),

kie τ = (1+√5)/2 estas la ora proporcio.

Geometriaj rilatoj

La rombo-dudek-dekduedro komunigas sian situon de verticoj kun 3 nekonveksaj unuformaj pluredroj kaj kun la unuformaj kombinaĵoj de 6 aŭ 12 stelokvinlateraj prismoj:

Malgranda dekdu-dudek-dekduedro

Malgranda rombo-dekduedro

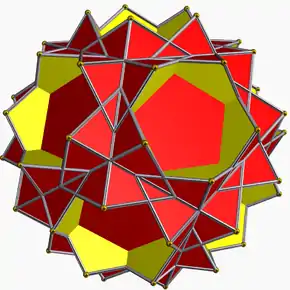Malgranda steligita senpintigita dekduedro

Solidoj de Johnson surbaze de la rombo-dudek-dekduedro estas:

Jn	Nomo	Bildo
72	Turnita rombo-dudek-dekduedro
73	Paraleloduturnita rombo-dudek-dekduedro
74	Najbaroduturnita rombo-dudek-dekduedro
75	Triturnita rombo-dudek-dekduedro
76	Malkreskigita rombo-dudek-dekduedro
77	Paraleloturnita malkreskigita rombo-dudek-dekduedro
78	Najbaroturnita malkreskigita rombo-dudek-dekduedro
79	Duturnita malkreskigita rombo-dudek-dekduedro
80	Paralelodumalkreskigita rombo-dudek-dekduedro
81	Najbarodumalkreskigita rombo-dudek-dekduedro
82	Turnita dumalkreskigita rombo-dudek-dekduedro
83	Trimalkreskigita rombo-dudek-dekduedro

Vidu ankaŭ

• Dekduedro
• Dudekedro
• Dudek-dekduedro
• Rombokub-okedro
• Senpintigita dudek-dekduedro (granda rombo-dudek-dekduedro)

Referencoj

• Williams, Robert. (1979) The Geometrical Foundation of Natural Structure: A Source Book of Design - La Geometria Fundamento de Natura Strukturo: Fonta Libro de Dizajno. Dover Publications, Inc. ISBN 0-486-23729-X. (Sekcio 3-9)

Eksteraj ligiloj

• Eric W. Weisstein, Malgranda rombo-dudek-dekduedro en MathWorld.
• La unuformaj pluredroj
• Virtualaj realaj pluredroj - la enciklopedio de pluredroj