Pluredra notacio de Conway

En geometrio, pluredra notacio de Conway estas maniero por priskribi pluredrojn per vico de operacioj farataj je la fonta pluredro. La notacio konsistas el la finaj signoj prezentataj la fontan pluredron kaj antaŭ ili estas signoj prezentataj la operaciojn, kiu estas aplikataj en la ordo dedekstre maldekstren.

La operacioj povas generi ĉiujn arĥimedajn solidojn kaj katalanajn solidojn el la platonaj solidoj. Aplikante pli longajn seriojn de ĉi tiuj operacioj, eblas krei multajn pli malsimplajn pluredrojn.

Ĝenerale ĉiu pluredro, kiu povas esti priskribita per notacio de Conway, havas plurajn notaciajn prezentojn.

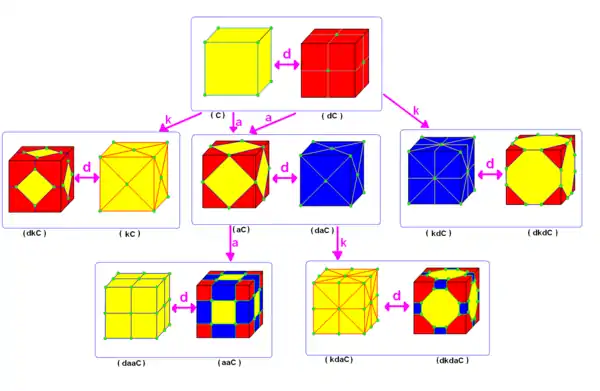11 novaj formoj povas esti derivitaj surbaze de la kubo uzante 3 operaciojn. La novaj pluredroj estas montrita kiel mapoj sur la surfaco de la kubo. Verticoj estas markitaj per verdaj cirkletoj.

Fontaj pluredroj

La fonta pluredro povas esti:

Platona solido:
- T - kvaredro
- O - okedro
- C - kubo
- I - dudekedro
- D - dekduedro
Pn - n-latera prismo
An - n-latera kontraŭprismo
Yn - n-latera piramido.

Ĝenerale ĉiu konveksa pluredro povus servi kiel la fonta ĉar la operacioj povas esti faritaj sur ĝi, kvankam en la notacio ne estas signoj por priskribi ĉi tion.

Operacioj je pluredroj

d	dualigo - ĉiu vertico kreas novan edron
tn	senpintigo de ĉiu n-obla vertico; se n ne estas skribita do senpintigo de ĉiuj verticoj
a	rektigo - tranĉo ĝis la lateraj mezpunktoj, ĉiu vertico kreas novan edron.
e	"elvolvo" - laterotranĉo - ĉiu vertico kreas novan edron kaj ĉiu latero kreas novan kvarlateran edron
s	riproĉigo - ĉiu vertico kreas novan edron kaj ĉiu latero kreas du novaj triangulajn edrojn.

Iuj oftaj kombinaĵoj de operatoroj havas pli mallongan notacion (ĉi tie X estas iu pluredro):

kn	knX = dtndX	piramidigo - kreo de piramido sur ĉiu n-latera edro; se n ne estas skribita do kreo de piramido sur ĉiu edro.
g	ĝ = dŝ	ĉiu n-latera edro estas dividita en n kvinlaterojn
o	oX = deX	ĉiu n-latera edro estas dividita en n kvarlaterojn.
j	ĵ = daX	kunigo - nova kajta edro estas kreita anstataŭ ĉiu latero
b	bX = taX	lateroverticotranĉo - ĉiu vertico kreas novan edron kaj ĉiu latero kreas novan kvarlateran edron
m	mX = dbX = kĵ	ĉiu n-latera edro estas dividita en 2n triangulojn

Ĉiu operacio konservas simetrion escepte de s kaj g, kiuj perdas la reflektan simetrion.

Ekzemploj

La operacioj estas aplikataj simile al funkcioj de dekstre maldekstren. Ekzemple:

Kubo estas C
Kubokedro, kiu estas rektigo de kubo, estas aC
Granda rombokub-okedro, kiu estas senpintigo de kubokedro, estas t4aC aŭ taC
Senpintigo de granda rombokub-okedro estas tt4aC aŭ ttaC

Genero de regulaj pluredroj

Ĉiu el la kvin konveksaj regulaj pluredroj havas propran simbolon, sed tamen povas esti skribita alimaniere:

Surbaze de triangula piramido Y3:
- T = Y3 (kvaredro = triangula piramido)
- O = aY3 (okedro = rektigita kvaredro)
- C = daY3 (kubo = duala de rektigita kvaredro)
- I = sY3 (dudekedro = riproĉa kvaredro)
- D = dsY3 (dekduedro = duala de riproĉa kvaredro)
Surbaze de triangula kontraŭprismo A3:
- O = A3 (okedro = triangula kontraŭprismo)
- C = dA3 (kubo = duala de okedro)
Surbaze de kvadrata prismo P4:
- C = P4 (kubo = (speciala) kvadrata prismo)
Surbaze de kvinlatera kontraŭprismo A5:
- I = k5A5 (dudekedro = turnoplilongigita 5-latera dupiramido)
- D = t5dA5 (dekduedro = senpintigita 5-latera kajtopluredro)

Pluredroj kun okedra simetrio

La kubo povas generi ĉiujn konveksajn unuformajn pluredrojn kaj katalanajn solidojn kun okedra simetrio.

En la tabelo la unuaj sep figuroj estas respektive dualaj al la duaj sep.

Kubo C	Kubokedro aC = djC	Senpintigita kubo tC = dkdC	Senpintigita okedro tdC = dkC
Malgranda rombokub-okedro eC = aaC = doC	Granda rombokub-okedro bC = dmC = taC = dkjC	Riproĉa kubo sC = dgC

Okedro dC	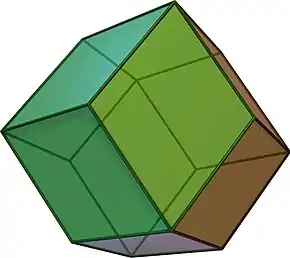Romba dekduedro jC = daC	Trilateropiramidigita okedro kdC = dtC	Kvarlateropiramidigita kubo kC = dtdC
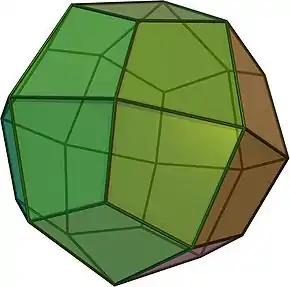Deltosimila dudekkvaredro oC = deC	Piramidigita dekduedro mC = dbC = kjC	Kvinlatera dudekkvaredro gC = dsC

Vastigaĵoj

Multaj interesaj pli malsimplaj pluredroj bezonas novajn operaciojn por sia konstruado.

La proponitaj de George W. Hart aldonaj operacioj estas:

p - "helico" - turnada operacio kiu kreas kvarlaterojn je la verticoj, ĉi tiu operacio estas mem-duala: dpX = pdX.
r - reflekto - faras la spegulan bildon, ĝi efikas nur se la figuro estas nememspegulsimetria pro operacio s aŭ p.

Vidu ankaŭ

Subdivida surfaco de Doo-Sabin - la e operacio
Subdivida surfaco de Catmull-Clark - la o operacio
Operacioj je hiperpluredroj kaj kahelaroj:
- Tranĉo t_{0, 1}{p, ...}
- Laterotranĉo t_{0, 2}{p, q, ...}
- Lateroverticotranĉo t_{0, 1, 2}{p, q, ...}
- Edrotranĉo t_{0, 3}{p, q, r, ...}
- Edroverticotranĉo t_{0, 1, 3}{p, q, r, ...}
- Edrolaterotranĉo t_{0, 2, 3}{p, q, r, ...}
- Edrolateroverticotranĉo t_{0, 1, 2, 3}{p, q, r, ...}
- Ĉelotranĉo t_{0, 4}{p, q, r, s, ...}
- Entutotranĉo t_{0, 1, ..., n-1}{p₁, p₂, ..., p_n-1}
- Rektigo t₁{p, ...}
- Dutranĉo t_{1, 2}{p, q, ...}
- Alternado
- Riproĉigo
Simbolo de Schläfli - etendita simbolo de Schläfli priskribas rezultojn de la operacioj faritaj je regulaj hiperpluredroj kaj regulaj kahelaroj

Eksteraj ligiloj

Eric W. Weisstein, Pluredra notacio de Conway en MathWorld.
Pluredra notacio de Conway Arkivigite je 2006-12-16 per la retarkivo Wayback Machine
George Olshevsky, Piramidigo en Glossary for Hyperspace. - la k operacio
George Olshevsky, Tranĉo en Glossary for Hyperspace. - senpintigo, la t operacio
George Olshevsky, Rektigo en Glossary for Hyperspace. - la a operacio
Interpretilo de George W. Hart - generas VRML modelojn laŭ pluredra notacio de Conway
George W. Hart, Skulptaĵoj surbaze de helicigitaj pluredroj, Paperoj de MOSAIC 2000, Seattle, WA, Aŭgusto 2000, pp. 61–70 - la p operacio

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.