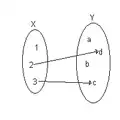
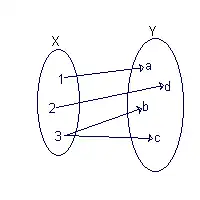
En matematiko, parta funkcio estas duvalenta rilato, kiu rilatigas ĉiun elementon de unu aro da matematikaj objektoj kun po ne pli ol unu elemento el la dua aro. Esence, tiel difinita nocio estas ekvivalenta al la ĝenerala senco de la matematika koncepto funkcio, kiu principe povas esti parta funkcio. Oni uzas la terminon parta funkcio en tiu ĉi vasta senco, kiam oni volas emfazi, ke konsiderataj funkcioj ne nepre estas (sed iuj inter ili povas esti) ĉie difinitaj (aŭ, sinonime, totalaj aŭ ĉieaj).

En la strikta senco, parta funkcio estas funkcio, kiu ne estas ĉie difinita. Tiun sencon oni kutime aplikas, kiam temas pri konkreta funkcio.

Parta funkcio kun fonta aro {1,2,3}, cela aro {a,b,c,d}, argumentaro {2,3} kaj bildaro {c,d}

Formalaj difinoj

X kaj Y estu aroj. Oni diras, ke funkcio f ĵetas X al Y, simbole

${\displaystyle f:X\to Y}$

se f estas tia rilato super ${\displaystyle X\times Y}$, ke por ĉiu ${\displaystyle x\in X}$ en f ekzistas ne pli ol unu duopo ${\displaystyle (x,y)\in f}$; en tia okazo oni skribas ${\displaystyle y=f(x)}$.

La aron X oni nomas la fonta aro; la aron Y, la cela aro, simbole iam E(f).

La aron de ĉiuj valoroj de funkcio f oni nomas ĝia bildaro aŭ simple bildo, simbole iam Im(f) (mallongigo de la anglalingva vorto image), kaj la aron de ĉiuj x en X, por kiuj f estas difinita, oni nomas ĝia malbildo aŭ argumentaro, simbole iam Dom(f) (mallongigo de la anglalingva vorto domain) aŭ D(f).

La funkcio ${\displaystyle f:X\to Y}$ nomiĝas ĉie difinita, ĉiea aŭ totala, se ĝi estas difinita sur la tuta aro X, t.e. se ĝia malbildo koincidas kun ĝia tuta fonta aro. Tio estas la malo de la strikta senco de la termino parta funkcio, kiu implicas, ke la funkcio ne estas ĉie difinita.

Sendependa variablo (la argumento) - la variablo, por ĉiu el kies unuopa valoro povas ekzisti (sola) responda valoro de funkcio.

Dependa variablo (la rezulto) - la variablo donita per la valoroj de la funkcio; ekz. en la funkcio y = sin(x), x - estas la sendependa variablo (argumento), dum y estas dependa variablo.

Oni povas difini partan funkcion per diversaj rimedoj:

• Tabela - per la vicoj de argumentoj kaj de respondaj valoroj de la funkcio;
• Grafika - la ordigitaj paroj (x, y), kiuj formas la funkcion, povas esti presentita kiel punktoj M(x, y) de la kartezia sistemo por vidigi la grafikaĵon, en la formo de la linio;
• Analitika - per egalaĵa formulo: ekzemple, y = 1/x.

Ekzemploj kaj malekzemploj

• La rilato, kiu rilatigas ĉiun personon kun ties aĝo, estas totala funkcio de la aro de homoj al la aro de naturaj nombroj, ĉar ĉiu persono havas ununuran aĝon.

• La rilato, kiu rilatigas ĉiun reelan nombron kun ĝia inverso, estas parta funkcio de la aro de reelaj nombroj al ĝi mem, ĉar ĝi ne estas difinita por ${\displaystyle x=0}$. Ĝi povas esti priskribita jene: ${\displaystyle f(x)=1/x}$ por ĉiuj ${\displaystyle x}$ ≠ ${\displaystyle 0}$.

• La rilato, kiu rilatigas ĉiun personon kun la lando, en kiu li estas civitano, entute ne estas funkcio (totala aŭ parta), ĉar ekzistas homoj kun pluraj civitanecoj.

• La rilato, kiu rilatigas ĉiun personon kun ties oficiala ŝakrango, estas parta sed ne ĉiea/totala funkcio, ĉar ekzistas homoj, kiuj ne estas rangitaj de FIDE aŭ alia ŝak-organizaĵo.

Vidu ankaŭ

• Grafikaĵo
• Disĵeto
• Surĵeto
• Dissurĵeto

Eksteraj ligiloj