| Mysterium Cosmographicum | |
|---|---|
 | |
| skribita verko | |
| Aŭtoroj | |
| Aŭtoro | Johano Keplero |
| Lingvoj | |
| Lingvo | Nov-Latino |
| Eldonado | |
| Eldondato | 1595 |
| Ĝenro | vulgarigo de scienco |
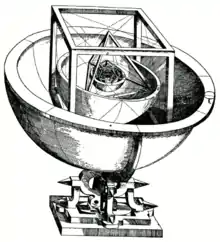
Mysterium Cosmographicum (laŭvorte La kosmografia mistero,[1] alternative tradukita kiel Kosma mistero, La sekreto de la mondo, aŭ ankaŭ per ioma variaĵo) estas libro pri astronomio de la germana astronomo Johannes Kepler, publikigita en Tubingeno en 1597[2], kvankam la titolpaĝo de la libro indikas 1596 kiel ties publikiga jaro,[2] kaj en dua eldono en 1621. Kepler proponis, ke la distancaj rilatoj inter la ses planedoj tiam konataj povas esti komprenataj laŭ terminoj de la kvin Platonaj solidoj, enfermitaj ene de sfero kiu reprezentis la orbiton de Saturno.
Tiu libro klarigas la kosmologian teorion de Keplero, bazita sur la Kopernika sistemo, en kiu la kvin Platonaj solidoj diktas la strukturon de la universo kaj montras la planojn de Dio pere de geometrio. Tiu fakte estis la dua klopodo ekde Koperniko kiu diris, ke la teorio de suncentrismo estas fizike prava.[3] Thomas Digges estis jam publikigante defendon de Koperniko en apendico en 1576. Laŭ la rakonto de la propra Keplero mem, li hazarde malkovris la bazon de la modelo demonstrante la geometrian rilaton inter du cirkloj.
Kepler asertis, ke li havis epifanion (subita scienca rimarko) la 19an de Julio 1595, dum instruado en Graz, demonstranta la periodan konjunkcion de Saturno kaj Jupitero en la zodiako: li konstatis, ke regulaj plurlateroj ligitaj unu enmetita kaj unu ĉirkaŭmetita cirklas je difinitaj proporcioj, kio, li raciigis, povus esti la geometria bazo de la universo. Post malsukceso trovi unikan aranĝon de plurlateroj kiuj kongruas kun konataj astronomiaj observoj (eĉ kun kromaj planedoj aldonitaj al la sistemo), Kepler ekeksperimentis per 3-dimensiaj pluredroj. Li trovis, ke ĉiu el la kvin Platonaj solidoj povus esti enmetita kaj ĉirkaŭmetita fare de ĉielaj sferoj; fiksante tiujn solidojn, ĉiuj enmetitaj en po unu sfero, unu ene de alia produktus ses tavolojn, korespondantaj al la ses tiam konataj planedoj — Merkuro, Venuso, Tero, Marso, Jupitero, kaj Saturno. Ordigante la solidojn laŭelekte — okedro, dudekedro, dekduedro, kvaredro, kubo — Kepler trovis, ke la sferoj povus esti metitaj je intervaloj korespondantaj al la relativaj grandoj de la vojo de ĉiu planedo, akceptante, ke la planedoj cirklas la Sunon. Kepler trovis ankaŭ formulon rilatiganta la grandon de la orbito de ĉiu planedo al la longo de ties orbita periodo: el internaj al eksteraj planedoj, la proporcio de pliigo en orbita periodo esats dufoje la diferenco en orbita radiuso. Tamen, Kepler poste malakceptis tiun formulon, ĉar ĝi ne estis sufiĉe preciza.[4]

Kiel indikita en la titolo, Kepler kredis, ke li estis malkovranta la geometrian planon de Dio por la universo. Multo de la entuziasmo de Kepler por la Kopernika sistemo venis el siaj teologiaj konvinkoj pri la konekto inter tio fizika kaj tio spirita; la universo mem estis imago de Dio, dum la Suno korespondus al la Patro, la stela sfero al la Filo, kaj la intervena spaco intera la Sankta Spirito. Lia unua manuskripto de Mysterium enhavis etendan ĉapitron kunigantan heliocentrismon kun bibliaj fragmentoj kiuj ŝajnis apogi geocentrismon.[5]
Kun la subteno de sia mentoro Michael Maestlin, Kepler ricevis permeson el la senato de la Tubingena universitato por publikigi sian manuskripton, kondiĉe de la forigo de la Biblia ekzegezo kaj de la aldono de pli simpla, pli komprenenbla priskribo de la Kopernika sistemo same kiel de la novaj ideoj de Keplero. Mysterium estis publikigita malfrue en 1596, kaj Kepler ricevis siajn ekzemplerojn kaj eksendis ilin al elstaraj astronomoj kaj patronoj komence de 1597; ĝi ne estis amplekse legita, sed ĝi establis la reputacion de Keplero kiel tre lerta astronomo. La entuziasma dediĉaĵo al povegaj patronoj kaj al la homoj kiuj kontrolis lian postenon en Graz, ankaŭ havigis gravan aliron al la patrona sistemo.[6]
Kvankam la detaloj estis modifitaj de lia posta verkaro, Kepler neniam abandonis la platonisman pluredr-sferecan kosmologion de Mysterium Cosmographicum. Liaj postaj ĉefaj astronomiaj verkoj estis iel nur pluaj disvolvigoj de tiu, rilate al la trovo de pli precizaj internaj kaj eksteraj dimensioj de la sferoj kalkulante la ekstercentrecojn de la planedaj orbitoj en ĝi. En 1621, Kepler publikigis etendan duan eldonon de Mysterium, duone tiom longa denove kiel la unua, detalanta en piednotoj la korektojn kaj plibonigojn kiujn li estis atingintajn en la 25 jaroj ekde ties unua publikigo.[7]
Notoj
- ↑ La kompleta titolo estis Prodromus dissertationum cosmographicarum, continens mysterium cosmographicum, de admirabili proportione orbium coelestium, de que causis coelorum numeri, magnitudinis, motuumque periodicorum genuinis & proprijs, demonstratum, per quinque regularia corpora geometrica (Indikilo de kosmologiaj eseoj, kiu enhavas la sekreton de la Universo; pri la mirinda proporcio de la ĉielaj sferoj, kaj pri la veraj kaj partikularaj kaŭzoj de la nombroj, grandoj, kaj periodaj movoj de la ĉieloj; establita per rimedoj de la kvin regulaj geometriaj solidoj).
- 1 2 Livio, Mario. [2002] (2003) The Golden Ratio: The Story of Phi, the World's Most Astonishing Number, 1‑a eldono, New York City: Broadway Books, p. 145. ISBN 0-7679-0816-3.
- ↑ James R. Voekel. "Classics of Astronomy by Johannes Kepler". chapin.williams.edu. 2010.
- ↑ Caspar. Kepler, pp. 60–65; vidu ankaŭ: Barker kaj Goldstein, "Theological Foundations of Kepler's Astronomy."
- ↑ Barker kaj Goldstein. "Theological Foundations of Kepler's Astronomy," pp. 99–103, 112–113.
- ↑ Caspar. Kepler, pp. 65–71.
- ↑ Field. Kepler's Geometrical Cosmology, Chapter IV, p 73ff.
Bibliografio
- Dreyer, J. L. E., A History of Astronomy from Thales to Kepler, Dover Publications, 1953, pp. 331, 377–379.