Tiuj ĉi plonĝistinoj minimumigas sian inercimomanton per alproksimigo de la kruroj al la korpo, tiel maksimumigante sian turniĝrapidon.

En fiziko, la inercimomanto (aŭ inertmomanto) estas grando, kiu mezuras la reziston de objekto al ŝanĝo de turniĝrapido. Ĝi ne nur dependas de la maso de la turniĝanta objekto, sed ankaŭ de la pozicio de la maso rilate al la turniĝakso.

La inercimomanto de objekto, konsistanta el n maseroj m_i lokataj al distancoj r_i de la turniĝakso z, difinatas kiel

${\displaystyle I_{z}=\sum _{i=1}^{n}m_{i}r_{i}^{2}}$.

La koncepton inercimomanto enkondukis la svisa matematikisto kaj fizikisto Leonhard Euler en sia verkaĵo Theoria motus corporum solidorum seu rigidorum ("Teoria movo de solidaj korpoj"), en 1765.

Laŭ la internacia mezurunuaro, la mezurunuo de inercimomanto estas ${\displaystyle kg*m^{2}}$.

La inercimomanto ludas, en turniĝoj, la saman rezistantan rolon, kiun la maso alprenas okaze de rektaj moviĝoj.

Precipaj momantoj de simplaj geometriaj korpoj

La peza punkto de la geometria korpo sur la akso de rotacio, al kiu la momanto de inercio raportas, ${\displaystyle m}$ estas la maso de la turniĝanta korpo. La momanto de inercio por rotacioj pri aliaj aksoj, oni povas tiam uzi la leĝon de Steiner, laŭ kiu oni devas aldoni la momanton rilatante al la distanco inter la du aksoj.

Bildo	Klarigo	Inercimomanto
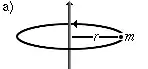	Punkta maso je distanco ${\displaystyle r}$ pri akso de rotacio.	${\displaystyle J=m\cdot r^{2}}$
	Masiva maldika disko, kiu turniĝas ĉirkaŭ sia akso de simetrio orta al sia ebeno; ĉar ${\displaystyle \scriptstyle d\ll r}$, d ne aperas en la proksimuma formulo.	${\displaystyle J\approx {1 \over 2}m\cdot r^{2}}$
	Maldika cilindra tubo, kiu turniĝas ĉirkaŭ sia akso de simetrio; ĉar ${\displaystyle \scriptstyle d\ll r}$, d ne aperas en la proksimuma formulo.	${\displaystyle J\approx m\cdot r^{2}}$[1]
	Masiva cilindro, kiu turniĝas ĉirkaŭ sia akso de simetrio.	${\displaystyle J={1 \over 2}m\cdot r^{2}}$[1]
	Cilindra tubo, kiu turniĝas ĉirkaŭ sia akso de simetrio; ${\displaystyle r_{1}=r_{2}=r}$ kondukas al la formulo pri maldika cilindra tubo.	${\displaystyle J=m{\frac {r_{1}^{2}+r_{2}^{2}}{2}}}$[2][3]
	Masiva cilindro, kiu turniĝas ĉirkaŭ transversa akso (duobla simetriakso) .	${\displaystyle J={1 \over 4}m\cdot r^{2}+{1 \over 12}m\cdot l^{2}}$[3]
	Maldika cilindra tubo, kiu turniĝas ĉirkaŭ transversa akso (duobla simetriakso).	${\displaystyle J={1 \over 2}m\cdot r^{2}+{1 \over 12}m\cdot l^{2}}$[4]
	Maldika cilindra tubeto, kiu turniĝas ĉirkaŭ centrita transversa akso (duobla simetriakso); ĉi tiu formulo estas proksimuma kalkulo por cilindra tubo kun ${\displaystyle \scriptstyle r\ll l}$.	${\displaystyle J={1 \over 12}m\cdot l^{2}}$[3]
	Maldika cilindra tubeto, kiu turniĝas ĉirkaŭ transversa akso orta al sia flanko.	${\displaystyle J={1 \over 3}m\cdot l^{2}}$[5]
	Sfera konko, kiu turniĝas ĉirkaŭ iu akso tra sia centro; ĉar ${\displaystyle \scriptstyle d\ll r}$, d ne aperas en la proksimuma formulo.	${\displaystyle J\approx {2 \over 3}m\cdot r^{2}}$[1]
	Masiva sfero, kiu turniĝas ĉirkaŭ iu akso tra sia centro.	${\displaystyle J={2 \over 5}m\cdot r^{2}}$[1]
	Orta paralelepipedo, kiu turniĝas ĉirkaŭ akso tra la centro, kiu estas paralela al la faco c.	${\displaystyle J={1 \over 12}m\cdot (a^{2}+b^{2})}$[1]
	Masiva konuso, kiu turniĝas ĉirkaŭ sia simetriakso.	${\displaystyle J={3 \over 10}m\cdot r^{2}}$[3]
	Konusa surfaco, kiu turniĝas ĉirkaŭ sia akso; la egaleco kun la inercion de masiva cilindro eblas pensigi, ke oni povas "platigi" ĉiun konuson ĝis cirkla disko, sen ŝanĝi lian momanton de inercio.	${\displaystyle J={1 \over 2}m\cdot r^{2}}$
	Masiva trunko de konuso, kiu turniĝas ĉirkaŭ sia akso.	${\displaystyle J={3 \over 10}m\cdot {(r_{1}^{5}-r_{2}^{5}) \over (r_{1}^{3}-r_{2}^{3})}}$[6]
	Masiva ringo kun centra radiuso R kaj duondikeco r, kiu turniĝas ĉirkaŭ sia simetriakso (tiel, la ekstera radiuso egalas al R+r)	${\displaystyle J=m\left({\frac {3}{4}}\cdot r^{2}+R^{2}\right)}$[7]

Referencoj

Vidu ankaŭ

• Momanto
• Momanto de forto