Kvaredro
Plia nomo	Triangula piramido
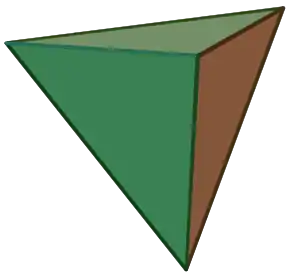Klaku por rigardi turnantan bildon
Speco	Trianguledra pluredro 3-simplaĵo
Vertica figuro	3.3.3
Bildo de vertico
Bildo de reto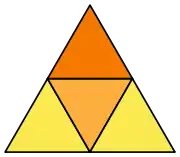
Simbolo de Wythoff	3 | 2 3
Simbolo de Schläfli	{3,3}
Figuro de Coxeter-Dynkin
Indeksoj	U01 C15 W1
Simbolo de Bowers	Tet
Verticoj	4
Lateroj	6
Edroj	4
Edroj detale	4{3}
χ	2
Geometria simetria grupo	Td
Duedra angulo	arccos(1/3) ~= 70,528779°
Duala	Mem-duala
Bildo de duala

Kvaredro estas pluredro komponita el 4 triangulaj edroj. Tri edroj kuniĝas je ĉiu vertico. Regula kvaredro estas kvaredro ĉe kiu la trianguloj estas regulaj. Regula kvaredro estas regula pluredro, unu el la platonaj solidoj.

Ekzistas nur unu speco de nedegenera kvaredro, kiu estas triangula piramido, alivorte ĉi ĉiuj kvaredroj estas topologie la samaj. Tamen degenera kvaredro povas esti topologie malsama, ekzemple ĝi povas esti subspeco de duvertica pluredro kun 4 edroj.

Surfaca areo kaj volumeno

La surfaca areo A kaj la volumeno V de regula kvaredro de randa longo a estas

${\displaystyle A=a^{2}{\sqrt {3}},}$

${\displaystyle V={\begin{matrix}{1 \over 12}\end{matrix}}a^{3}{\sqrt {2}}.}$

La alto estas ${\displaystyle \scriptstyle {h={\sqrt {6}}(a/3)}}$.

La angulo inter latero kaj edro estas arctan (2^1/2) (proksimume 55°), angulo inter du edroj estas arccos(1/3) = arctan(2^3/2) (proksimume 71°). La angulo de la centro al ĉiu du verticoj estas arccos(-1/3) (proksimume 109,47°).

Ĉar kvaredro estas triangula piramido ĝia volumeno estas ${\displaystyle \scriptstyle {V={\frac {1}{3}}Ah}}$ kie A estas la areo de la bazo kaj h la alto de la bazo al la supro. Ĉi tio aplikas (kaj donas la saman rezulton) por ĉiu el la kvar elektoj de la bazo, do la distancoj de la verticoj al la kontraŭaj edroj estas inverse proporciaj kun la areoj de ĉi tiuj edroj.

Ankaŭ, por kvaredro ABCT la volumeno estas

${\displaystyle V={\frac {AT\cdot BT\cdot CT}{6}}}$

${\displaystyle \cdot {\sqrt {1+2\cdot \cos a\cdot \cos b\cdot \cos c-\cos ^{2}a-\cos ^{2}b-\cos ^{2}c}}}$

kie a estas angulo ATB, b estas angulo BTC, kaj c estas angulo CTA.

(Ĉiu, Iu) du kontraŭaj randoj de kvaredro (mensogi, kuŝi) sur du deklivaj linioj. Se la plej proksima paro de punktoj inter ĉi tiuj du linioj estas punktoj en la randoj, ili difini la distanco inter la randoj; alie, la distanco inter la randoj egalaj (tiu, ke, kiu) inter unu el la (finpunktoj, finaj punktoj) kaj la kontraŭa rando.

La volumeno de kvaredro, kun verticoj a, b, c kaj d, estas

V = (1/6)·|det(a−b, b−c, c−d)|

aŭ

${\displaystyle V={\frac {|(\mathbf {d} -\mathbf {a} )\cdot ((\mathbf {d} -\mathbf {b} )\times (\mathbf {d} -\mathbf {c} ))|}{6}}.}$ (^[1])

Ankaŭ, se d_ij estas distancoj inter di verticoj de kvaredro, ĝia volumeno estas:

${\displaystyle 288\cdot V^{2}={\begin{vmatrix}0&1&1&1&1\\1&0&d_{12}^{2}&d_{13}^{2}&d_{14}^{2}\\1&d_{21}^{2}&0&d_{23}^{2}&d_{24}^{2}\\1&d_{31}^{2}&d_{32}^{2}&0&d_{34}^{2}\\1&d_{41}^{2}&d_{42}^{2}&d_{43}^{2}&0\end{vmatrix}}}$

Se la determinanta valoro estas negativa do ne eblas konstrui kvaredron kun la donita distancoj inter la verticoj.

Geometriaj rilatoj

Kvaredro estas 3-simplaĵo. Malsimile al la aliaj platonaj solidoj, ĉiuj verticoj de regula kvaredro estas samdistancaj de unu la alia (ili estas en la sola ebla ordigo de kvar samdistancaj punktoj).

Kvaredro estas mem-duala pluredro.

Regula kvaredro povas esti enigita en kubon je du manieroj tiel ke ĉiu vertico estas vertico de la kubo, kaj ĉiu latero estas diagonalo de unu el la kubaj edroj. Por unu tia enigo, la karteziaj koordinatoj de la verticoj estas

(+1, +1, +1);

(-1, -1, +1);

(-1, +1, -1);

(+1, -1, -1).

Por la alia kvaredro (kiu estas duala al la unua), ĉiuj signoj estas la malaj.

La kvaredro estas unika inter la unuformaj pluredroj en ne havo de paralelaj edroj.

• 
  Senpintigita kvaredro
• 
  Du kvaredroj en kubo
• 
  Kombinaĵo de kvin kvaredroj
• 
  Kombinaĵo de dek kvaredroj

Uzoj

La amonia molekulo estas kvaredra

• La kvaredra formo estas estadas en naturo en molekuloj. Ekzemple en metana molekulo CH₄ la kvar hidrogenaj atomoj kuŝas en verticoj de kvaredro kaj la karbona atomo estas en la centro.

Vidu ankaŭ

• Kvinĉelo - 4-dimensia analogo de kvaredro
• Simplaĵo (geometrio) - n-dimensia analogo de kvaredro
• Unuformaj pluredraj kombinaĵoj de kvaredroj
  • Kombinaĵo de 6 kvaredroj kun turna libereco
  • Kombinaĵo de 12 kvaredroj kun turna libereco
  • Kombinaĵo de 6 kvaredroj
  • Kombinaĵo de 2 kvaredroj
  • Kombinaĵo de 5 kvaredroj
  • Kombinaĵo de 10 kvaredroj
  • Prisma kombinaĵo de kontraŭprismoj kun turna libereco de p/q-lateraj kontraŭprismoj konsistas el kvaredroj se p=2, q=1
  • Prisma kombinaĵo de kontraŭprismoj de p/q-lateraj kontraŭprismoj konsistas el kvaredroj se p=2, q=1
• Leĝo de kosinusoj ankaŭ por kvaredro
• Leĝo de sinusoj ankaŭ por kvaredro
• Kvaredra nombro

Referencoj

Eksteraj ligiloj

• Eric W. Weisstein, Kvaredro en MathWorld.
• La unuformaj pluredroj
• Virtualaj realaj pluredroj
• Paperaj modeloj de pluredroj
• Miriga kvaredro
• kvaredra kerna reto Apliko de kvaredra strukturo por datuma reto