En matematiko kvadriko, aŭ kvadrika surfaco, estas D-dimensia hipersurfaco difinita kiel situo de nuloj de kvadrata polinomo. En koordinatoj ${\displaystyle \{x_{0},x_{1},x_{2},\ldots ,x_{D}\}}$ en D+1-dimensia spaco, la ĝenerala kvadriko estas difinita per la algebra ekvacio

${\displaystyle \sum _{i,j=0}^{D}Q_{i,j}x_{i}x_{j}+\sum _{i=0}^{D}P_{i}x_{i}+R=0}$

kie Q estas D+1 dimensia kvadrata matrico ne egala al la nula matrico kaj P estas D+1 dimensia vektoro kaj R estas nombro. Ĝenerale, la loko de nuloj de aro de polinomoj estas algebra diversaĵo. Kvadriko estas tial ekzemplo de algebra diversaĵo. Ĉiu projekcia diversaĵo povas esti montrita al esti izomorfia al la komunaĵo de aro de kvadrikoj.

En ne speciala okazo, la ununormigita ekvacio por du-dimensia (D=2) kvadriko tri-dimensia spaco centrita je la fonto (0, 0, 0) estas:

${\displaystyle \pm {x^{2} \over a^{2}}\pm {y^{2} \over b^{2}}\pm {z^{2} \over c^{2}}=1}$

Per movoj kaj turnoj ĉiu kvadriko povas esti konvertita al unu el kelkaj ununormigitaj formoj. En tri-dimensia eŭklida spaco, estas 17 ĉi tiaj ununormigitaj formoj:

Nomo	Aro de punktoj en reela spaco (se malsamas de la nomo)	Ekvacio	Bildo
elipsoido		${\displaystyle x^{2}/a^{2}+y^{2}/b^{2}+z^{2}/c^{2}=1}$
sferosimilaĵo (speciala okazo de elipsoido)		${\displaystyle x^{2}/a^{2}+y^{2}/a^{2}+z^{2}/b^{2}=1}$
sfero (speciala okazo de sferosimilaĵo)		${\displaystyle x^{2}/a^{2}+y^{2}/a^{2}+z^{2}/a^{2}=1}$
imaginara elipsoido	malplena aro	${\displaystyle x^{2}/a^{2}+y^{2}/b^{2}+z^{2}/c^{2}=-1}$
hiperboloido de unu folio		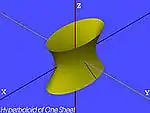${\displaystyle x^{2}/a^{2}+y^{2}/b^{2}-z^{2}/c^{2}=1}$
hiperboloido de du folioj		${\displaystyle x^{2}/a^{2}-y^{2}/b^{2}-z^{2}/c^{2}=1}$
imaginara konuso	punkto	${\displaystyle x^{2}/a^{2}+y^{2}/b^{2}+z^{2}/c^{2}=0}$
elipsa konuso		${\displaystyle x^{2}/a^{2}+y^{2}/b^{2}-z^{2}/c^{2}=0}$
cirkla konuso (speciala okazo de elipsa konuso)		${\displaystyle x^{2}/a^{2}+y^{2}/a^{2}-z^{2}/b^{2}=0}$
elipsa paraboloido		${\displaystyle x^{2}/a^{2}+y^{2}/b^{2}-z=0}$
cirkla paraboloido		${\displaystyle x^{2}/a^{2}+y^{2}/a^{2}-z=0}$
hiperbola paraboloido		${\displaystyle x^{2}/a^{2}-y^{2}/b^{2}-z=0}$
elipsa cilindro		${\displaystyle x^{2}/a^{2}+y^{2}/b^{2}=1}$
cirkla cilindro (speciala okazo de elipsa cilindro)		${\displaystyle x^{2}/a^{2}+y^{2}/a^{2}=1}$
imaginara elipsa cilindro	malplena aro	${\displaystyle x^{2}/a^{2}+y^{2}/b^{2}=-1}$
hiperbola cilindro		${\displaystyle x^{2}/a^{2}-y^{2}/b^{2}=1}$
du imaginaraj intersekcantaj ebenoj	rekto	${\displaystyle x^{2}/a^{2}+y^{2}/b^{2}=0}$
du intersekcantaj ebenoj		${\displaystyle x^{2}/a^{2}-y^{2}/b^{2}=0}$
parabola cilindro		${\displaystyle x^{2}/a^{2}+y=0}$
du paralelaj ebenoj		${\displaystyle x^{2}/a^{2}=1}$
du imaginaraj paralelaj ebenoj	malplena aro	${\displaystyle x^{2}/a^{2}=-1}$
du koincidantaj ebenoj	ebeno	${\displaystyle x^{2}/a^{2}=0}$

En reela projekcia spaco, la elipsoido, la elipsa paraboloido kaj la hiperboloido de du folioj estas ekvivalentaj unu al la alia supren al projekcia transformo. La du hiperbolaj paraboloidoj estas ne malsamaj de unu la alian (ĉi tiuj estas surfacoj konsistantaj el aroj de rektoj). La konuso kaj la cilindro estas ne malsamaj unu de la alia (ĉi tiuj estas degeneraj kvadrikoj ĉar ilia gaŭsa kurbeco estas nulo).

En kompleksa projekcia spaco ĉiuj nedegeneraj kvadrikoj estas nediferencigeblaj unu de la alia.

Vidu ankaŭ

• Koniko - 1-dimensia kvadriko en 2-dimensia ebeno
• Kvadrata funkcio

Eksteraj ligiloj

• Kvadrikoj Arkivigite je 2018-07-18 per la retarkivo Wayback Machine
• Kvadriko je MathWorld