Kubokedro
Klaku por rigardi turnantan bildon
Speco	kvazaŭregula
Vertica figuro	3.4.3.4
Bildo de vertico
Bildo de reto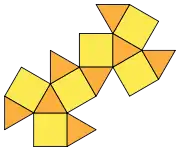
Simbolo de Wythoff	2 | 3 4 3 3 | 2
Simbolo de Schläfli	${\displaystyle {\begin{Bmatrix}3\\4\end{Bmatrix}}}$
Figuro de Coxeter-Dynkin
Indeksoj	U07 C19 W11
Simbolo de Bowers	Co
Verticoj	12
Lateroj	24
Edroj	14
Edroj detale	8{3}+6{4}
χ	2
Geometria simetria grupo	Oh
Duala	Romba dekduedro
Bildo de duala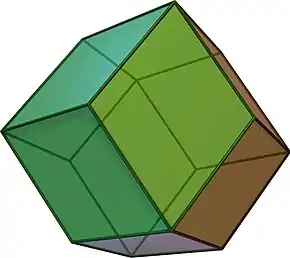

Kubokedro estas pluredro kun ok triangulaj edroj kaj ses kvadrataj edroj. Kubokedro havas 12 identajn verticojn, kun du trianguloj kaj du kvadratoj kuniĝantaj je ĉiu, kaj 24 identajn laterojn, kiuj ĉiu kunigas triangulon kaj kvadraton. Ĝi estas kvazaŭregula pluredro, arĥimeda solido, vertico-transitiva kaj latero-transitiva.

Aliaj nomoj

• Rektigita kubo
• Rektigita okedro
• Laterotranĉita kvaredro
• Triangula turnodukupolo

Areo kaj volumeno

La areo A kaj la volumeno V de la kubokedro de latera longo a estas:

${\displaystyle A=(6+2{\sqrt {3}})a^{2}\approx 9.46410162a^{2}}$

${\displaystyle V={\frac {5}{3}}{\sqrt {2}}a^{3}\approx 2.3570226a^{3}}$

Karteziaj koordinatoj

La karteziaj koordinatoj de verticoj de kubokedro de latera longo √2 centrita je (0,0,0) estas:

(±1,±1,0)

(±1,0,±1)

(0,±1,±1)

Geometriaj rilatoj

Kubokedro povas esti ricevita per preno de konvena sekco de kvar-dimensia kruco-hiperpluredro.

Kubokedro havas okedran simetrion. Ĝia unua steligo estas la kombinaĵo de kubo kaj ĝia duala okedro, kun la verticoj de la kubokedro situantaj je la mezpunktoj de la lateroj.

La kubokedro estas rektigita kubo kaj ankaŭ rektigita okedro.

Ĝi estas ankaŭ latervertictranĉita kvaredro. De ĉi tiu konstruado ĝi havas la simbolon de Wythoff: 3 3 | 2.

Latervertictranĉo de kvaredro

Diversampleksa latervertictranĉo de la kvaredro produktas pluredron kun edroj paralelaj al tiuj de la kubokedro, konkrete ok trianguloj de du ampleksoj, kaj ses ortanguloj. Kvankam iliaj lateroj estas neegalaj, ĉi tiu pluredro restas vertico-transitiva – ĝi havas la plenan kvaredran geometrian simetrian grupon kaj ĝiaj verticoj estas ekvivalentaj sub ĉi tiu grupo.

La randoj de kubokedro formas kvar regulajn seslaterojn. Se la kubokedro estas tranĉita per ebeno de unu el ĉi tiuj seslateroj, ĉiu duono estas triangula kupolo; la kubokedra mem tial povas nomiĝi ankaŭ kiel triangula turnodukupolo, la plej simpla de la serio (escepte la turnodufirsto, kiu estas degenera turnodukupolo). Se unu el la duonoj turni je 60 gradoj, rezultas triangula ortodukupolo.

Ambaŭ triangulaj dukupoloj estas gravaj en sfera pakado. La distanco de la pluredra centro al ĝiaj verticoj estas egala al ĝia latera longo. Centra sfero povas havi ĝis dek du najbarojn – sferojn kun centroj je la verticoj. En edro-centrita kuba krado la eroj havas la poziciojn de kubokedraj verticoj. En seslatere pakitaj kradoj ili esti konformaj laŭ la anguloj de la triangula ortodukupolo. En ambaŭ okazoj la centra sfero havas pozicion de la pluredra centro.

La romba tridekedro estas unu el la naŭ latero-transitivaj konveksaj pluredroj, ili estas 5 platonaj solidoj, kubokedro, dudek-dekduedro, romba dekduedro kaj romba tridekedro.

Kubokedroj aperas kiel ĉeloj en tri el la konveksaj unuformaj ĉelaroj kaj en naŭ el la konveksaj unuformaj plurĉeloj.

Duala pluredro de kubokedro estas la romba dekduedro.

La volumeno de la kubokedro estas 5/6 de tiu de la enmetanta kubo kaj 5/8 de tiu de la enmetanta okedro.

La kubokedro ekzistas en la aro de senpintigitaj formoj inter kubo kaj okedro:

Kubo	Senpintigita kubo	Kubokedro	Senpintigita okedro	Okedro

Vidu ankaŭ

• Kubo
• Dudek-dekduedro
• Okedro
• Rombokub-okedro
• Senpintigita kubokedro
• Triangula ortodukupolo
• Kombinaĵo de 5 kubokedroj
• Unua steligo de kubokedro

Referencoj

• Williams, Robert. (1979) The Geometrical Foundation of Natural Structure: A Source Book of Design - La Geometria Fundamento de Natura Strukturo: Fonta Libro de Dizajno. Dover Publications, Inc. ISBN 0-486-23729-X. (Sekcio 3-9)

Eksteraj ligiloj

• La unuformaj pluredroj
• Virtualaj realaj pluredroj - la enciklopedio de pluredroj