Por samtitola artikolo vidu la paĝon Funkcio de Dirichlet.

Funkcio η (aŭ funkcio η de Dirichlet — funkcio difinita por kompleksaj argumentoj, kiel:

${\displaystyle \eta (z)=\left(1-2^{1-z}\right)\zeta (z)}$

kaj ${\displaystyle \zeta (z)}$ - funkcio ζ de Riemann.

Ceteraj difinoj

• Difino per senfina serio:
•  :${\displaystyle \eta (z)=\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}}{n^{z}}}}$ .
• Difino per integralo:
•  :${\displaystyle \eta (z)={\frac {1}{\Gamma (z)}}\int \limits _{0}^{\infty }{\frac {x^{z-1}}{e^{x}+1}}\,dx}$
• :kaj ${\displaystyle \Gamma (z)}$ — funkcio Γ

Ecoj

• Reala parto de funkio η kaj reala parto de funkcio kun kompleksa konjugita argumento estas sama:
•  :${\displaystyle {\mbox{Re}}(\eta (z))={\mbox{Re}}(\eta (z^{*}))}$
• Imaginara parto de funkio kaj imaginara parto de funkio kun kompleksa konjugita argumento estas kontraŭa:
•  :${\displaystyle {\mbox{Im}}(\eta (z))=-{\mbox{Im}}(\eta (z^{*}))}$
• Limeso en senfino egalas 1:
•  :${\displaystyle \lim _{{\mbox{Re}}(z)\to \infty }\eta (z)=1}$
• Rekte videbla estas, ke (el supraj ecoj):
•  :${\displaystyle \lim _{Re(z)\to \infty }{\mbox{Re}}(\eta (z))=1}$
•  :${\displaystyle \lim _{Re(z)\to \infty }{\mbox{Im}}(\eta (z))=0}$ .

Grafikaĵoj

• 
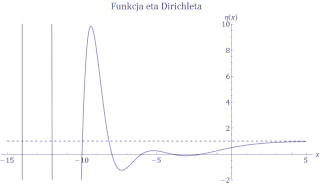  η(x) por realaj nombroj. Imaginara parto estas nulo
• 
  Grafikaĵo de funkcio η(z) por tuta kompleksa surfaco.