La artikolo estas parto de serio pri grafeoteorio.

Plej gravaj terminoj grafeo arbo subgrafeo ciklo kliko grado de vertico grado de grafeo Elektitaj klasoj de grafeoj plena grafeo plena dukolora grafeo kohera grafeo arbo grafeo dudividebla Fenda grafeo regula grafeo grafeo de Euler grafeo de Hamilton grafeo senrelifa pli... Grafeaj algoritmoj A* Bellman-Ford Dijkstry Fleury Floyd-Warshall Johnson Kruskal Prim traserĉado de grafeo – en larĝeco – en profundo plej proksima najbaro Problemoj prezentataj kiel grafeaj problemo de vojaĝisto problemo de ĉina leteristo problemo de marŝrutigado problemo de kunigado de geedzoj Aliaj kodo de Gray diagramo de Hasse kodo de Prüfer Reprezentado de grafeo Glosaro de grafeoteorio

Fenda grafeo disdividita en klikon kaj sendependan aron

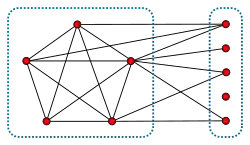
En grafeoteorio, fenda grafeo estas grafeo en kiu la verticoj povas esti disdividitaj en klikon kaj sendependan aron.

La dispartigo en klikon kaj sendependan aron ne nepre estas unika; ekzemple, la vojo a-b-c estas fenda grafeo, verticoj de kiu povas esti disdividitaj en tri malsamaj manieroj:

• kliko {a, b} kaj la sendependa aro {c}
• kliko {b, c} kaj la sendependa aro {a}
• kliko {b} kaj la sendependa aro {a, c}

Fendaj grafeoj povas esti karakterigitaj per iliaj konkluditaj subgrafeoj, grafeo estas fenda se kaj nur se neniu konkludita subgrafeo estas ciklo sur kvar aŭ kvin verticoj, aŭ paro de disaj lateroj (la komplemento de 4-ciklo).

Fendaj grafeoj estis unue studitaj de Földes kaj Hammer en du paperoj en 1977, kaj sendepende prezentitaj de Tiŝkeviĉ kaj Ĉernjak en 1979.

Rilato al aliaj grafeaj familioj

Komplemento de fenda grafeo estas denove fenda grafeo. Alia karakterigado de fendaj grafeoj estas per komplementigo: fenda grafeo estas ĥorda grafeo kies komplemento estas ankaŭ ĥorda. Ĝuste kiel ĥordaj grafeoj estas la komunaĵaj grafeoj de subarboj de arboj, fendaj grafeoj estas la komunaĵaj grafeoj de malsamaj substeloj de steloj. Preskaŭ ĉiuj ĥordaj grafeoj estas fendaj grafeoj, kiel Bender kaj aliaj en 1985 montris; tio estas, en la limigo kiam n strebas al malfinio, la frakcio de n-verticaj ĥordaj grafeoj kiuj estas fendaj proksimiĝas al 1. Ĉar ĥordaj grafeoj estas perfektaj, tiel fendaj grafeoj estas perfektaj. La duopa fendaj grafeoj, familio de grafeoj derivitaj de fendaj grafeoj per duobligo de ĉiu vertico (tiel la kliko iĝas kontraŭkongruantan kaj la sendependa aro iĝas kongruantan), estas unu el kvin bazaj klasoj de perfektaj grafeoj de kiu ĉiuj la aliaj povas esti formitaj en la pruvo de Ĉudnovski kaj aliaj en 2006 de la forta perfekta grafea teoremo.

Grafeo estas ambaŭ fenda grafeo kaj intervala grafeo se kaj nur se ĝia komplemento estas ambaŭ fenda grafeo kaj komparebleca grafeo. La fenda komparebleca grafeo, kaj pro tio ankaŭ la fenda intervala grafeo, povas esti karakterigita per aro de tri malpermesitaj konkluditaj subgrafeoj. La fenda kungrafeo estas akurate la sojla grafeo, kaj la fenda permuta grafeo estas akurate la intervala grafeo kiu havas intervalan grafeon kiel komplemento. Fenda grafeo havas kunkoloran nombron 2.

Maksimuma kliko kaj maksimuma sendependa aro

Estu G esti fenda grafeo, disdividita en klikon C kaj sendependan aron I. Tiam ĉiu maksimuma kliko en fenda grafeo estas C mem, aŭ la najbaraĵo de vertico en I. Tial ĉe fenda grafeo, estas facile identigi la maksimuman klikon, kaj ankaŭ la maksimuman sendependan aron per konsidero de komplementa grafeo. En ĉiu fenda grafeo, unu el la sekvaj tri eblecoj veras:

• C estas la maksimuma kliko kaj I estas la maksimuma sendependa aro. En ĉi tiu okazo, G havas unikan dispartigon (C, I) en klikon kaj sendependan aron.
• Tie ekzistas vertico x en I tia ke C ∪ {x} estas plena. En ĉi tiu okazo, C ∪ {x} estas la maksimuma kliko kaj I estas la maksimuma sendependa aro.
• Tie ekzistas vertico x en C tia ke I ∪ {x} estas sendependa. En ĉi tiu okazo, I ∪ {x} estas la maksimuma sendependa aro kaj C estas la maksimuma kliko.

Iuj optimumigaj problemoj, inkluzivante kolorigon de grafeo, kiuj estas NP-plenaj sur pli ĝeneralaj grafeoj, estas simplaj sur fendaj grafeoj.

Vico de gradoj de verticoj

Tio ĉu donita grafeo estas fenda povas esti kontrolite havante nur vicon de gradoj de ĉiuj ĝiaj verticoj. Tio estas ke supozu ke du grafeoj havas la propraĵon ke, por ĉiu i, ambaŭ grafeoj havas egale multajn verticojn de grado i (verticoj kun i najbaraj lateroj); tiam aŭ ambaŭ grafeoj estas fendaj aŭ ambaŭ ne estas fendaj. Pli detale, ordigu gradojn de verticoj en n-vertica grafeo G en la ordigitan vicon d₁ ≥ d₂ ≥ ... ≥ d_n, kaj estu m esti la plej granda valoro de i tia ke d_i ≥ i-1. Tiam G estas fenda grafeo se kaj nur se

${\displaystyle \sum _{i=1}^{m}d_{i}=m(m-1)+\sum _{i=m+1}^{n}d_{i}}$

En ĉi tiu okazo, la m verticoj kun la plej grandaj gradoj formas maksimuman klikon en G, kaj la ceteraj verticoj estas sendependa aro.

Kalkulado de fendaj grafeoj

Royle en 2000 montris ke fendaj grafeoj kun n nemarkitaj verticoj estas en dissurĵeta (unu al unu) rilato kun certaj familioj de Sperner. Uzante ĉi tiun rilaton, li donis formulon por la kvanto de neizomorfiaj fendaj grafeoj de n verticoj. Ĉi tiuj kvantoj por n=1, 2, 3, ... estas

1, 2, 4, 9, 21, 56, 164, 557, 2223, 10766, 64956, 501696, ...

Ĉi tiu rezulto estis sendepende pruvita pli frue de Tiŝkeviĉ kaj Ĉernjak en 1990.

Referencoj

• A048194 en OEIS - vico de kvantoj de neizomorfiaj fendaj grafeoj de n verticoj por n=1, 2, 3, ...

• Bender, E. A.; Richmond, L. B.; Wormald, N. C. (1985). “Almost all chordal graphs split - Preskaŭ ĉiuj ĥordaj grafeoj estas fendaj”, J. Austral. Math. Soc., Series A 38 (2), p. 214–221. MathSciNet0770128. 
• Maria Chudnovsky, Neil Robertson, Paul Seymour, Thomas, Robin (2006). “The strong perfect graph theorem - La forta perfekta grafea teoremo”, Annals of Mathematics - Analoj de matematiko 164 (1), p. 51–229. MathSciNet2233847. 
• Stéphane Földes, Peter L. Hammer (1977). “Split graphs having Dilworth number two - Fendaj grafeoj havanta nombron de Dilworth du”, Canad. J. Math. 29 (3), p. 666–672. MathSciNet0463041. 
• Peter L. Hammer, Bruno Simeone (1981). “The splittance of a graph - La fendeco de grafeo”, Combinatorica 1 (3), p. 275–284. doi:10.1007/BF02579333. MathSciNet0637832. 
• Merris, Russell (2003). “Split graphs - Fendaj grafeoj”, European J. Combin. 24 (4), p. 413–430. doi:10.1016/S0195-6698(03)00030-1. MathSciNet1975945. 
• Royle, Gordon F. (2000). “Counting set covers and split graphs - Kalkulaj araj kovroj kaj fendaj grafeoj”, Journal of Integer Sequences - Ĵurnalo de entjeraj vicoj 3 (2), p. 00.2.6. MathSciNet1778996.