En probablo-teorio, evento estas aro da rezultoj de hazardoprovoj (subaro de la provrezultaro), al kiu probablo estas atribuita. Tipe, ĉiu subaro de la provrezultaro estas evento (kio signifas, ke ĉiu ano de la aro de ĉiuj subaroj de la provrezultaro estas evento); tamen en difinado de probablospaco eblas ekskludi certajn subarojn de la provrezultaro el la klaso da eventoj (vidu sube).
Ekzemplo
Se oni havas kartaron el 52 ludkartoj kaj du ĵokeroj, kaj tiras unu karton el la kartaro, tiam la provrezultaro estas 54-elementa aro, ĉar ĉiu aparta karto prezentas eblan rezulton (observaĵon). Okazo, tamen, estas ĉiu subaro de la provrezultaro: interalie, eventoj, ke la elektita karto trafas al unu el jenaj aroj:
- ĉiu unuelementa aro konsistanta el unuopa individua karto (simpla okazaĵo, da kiuj estas 54, po unu prezentantaj la 54 eblajn kartojn de la kartaro);
- la malplena aro (kiu havas la probablon 0, ĉar tiu ĉi evento neniam okazas;
- la provrezultaro mem (la tuta aro el 54 kartoj, kiu havas la probablon 1, ĉar tiu evento nepre okazas);
- ĉiuj ceteraj propraj subaroj de la provrezultaro, enhavantaj plurajn elementojn. Tiel, ekzemple, inter la okazoj estas:
- «Ruĝa kaj nigra samtempe, sed ne ĵokero» (alia priskribo de la malplena aro),
- «Kera kvino» (1-elementa),
- «Reĝo» (4-elementa),
- «Figuro» (12-elementa),
- «Piko» (13-elementa),
- «Figuro aŭ ruĝa» (32-elementa),
- «Ajna karto» (54-elementa, la tuta aro).
Ĉar ĉiuj okazoj estas aroj, ili estas kutime skribataj kiel aroj (ekzemple {1, 2, 3}), kaj prezentataj grafike per Venn-aj diagramoj. Venn-aj diagramoj estas aparte utilaj por prezentado de okazoj, ĉar la probablon de la okazo eblas identigi kun la rilatumo de la areo de la okazo kaj la areo de la tuta provrezultaro. Ĉiu el la aksiomoj de probablo kaj la difino de kondiĉa probablo povas esti ilustrita en ĉi tia maniero.
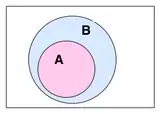 A estas subaro de B Venn-a diagramo de okazo. B estas la provrezultaro kaj A estas okazo. Laŭ la rilatumo de iliaj areoj, la probablo de A estas proksimume 0,4. |
Eventoj en probablospacoj
En la mezuro-teoria priskribo de probablospacoj, okazo povas esti difinita kiel ano de la σ-algebro sur la provrezultaro. Notu, tamen, ke ĉe ĉi tiu difino, ĉiu subaro de la provrezultaro kiu ne membras en la σ-algebro ne estas okazo, kaj ne havas probablon. Tamen ĉe racia difino de probablospaco ĉiu interesa okazo estas elemento la σ-algebro.