| Eratosteno de Kireno (276 a. K. - 194 a. K.) | |||||
|---|---|---|---|---|---|
 Bildo de Eratosteno de Cireno. | |||||
| Persona informo | |||||
| Ἐρατοσθένης ὁ Κυρηναῖος | |||||
| Naskonomo | Ἐρατοσθένης | ||||
| Naskiĝo | 276 a. K. en Cyrenae, antikva Greka urbo, nun apartenanta al Libio | ||||
| Morto | 194 a. K. en Aleksandrio, Egiptio | ||||
| Lingvoj | antikva greka vd | ||||
| Profesio | |||||
| Okupo | matematikisto • astronomo • poeto • bibliotekisto • historiisto • verkisto • muzikologo • muzika teoriisto • geografo • elegiisto • filozofo vd | ||||
| Laborkampo | geometrio • nombroteorio • geografio vd | ||||
| Verkado | |||||
| Verkoj | kribrilo de Eratosteno ❦ Catasterismi vd | ||||
| |||||
| vd | Fonto: Vikidatumoj | ||||
Eratosteno de Kireno (greke: Ἐρατοσθένης, Eratosthénês; naskiĝis ĉirkaŭ -276 en Aleksandrio, Egiptio; mortis ĉirkaŭ -194) estis greka astronomo, geografo, filozofo kaj matematikisto.
Li iĝis bibliotekestro de la Biblioteko de Aleksandrio ĉirkaŭ -230 laŭ peto de Ptolemeo la 3-a, faraono de Egiptio.
Pasia astronomo, blindiĝinte li lasis sin morti per malsato, ĉar li ne plu povis admiri la stelojn.[1].
La asteroido 3251 Eratosteno portas lian nomon.
Ĉirkaŭmezuro de la tero
Eratosteno en la jaro 225 kalkulis la ĉirkaŭmezuron de la tero.
Lia metodo
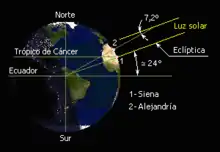
Eratosteno sciis, ke ĉiujare je la 21-an de junio en Syene (nuntempe Asuan) la suno staras tagmeze ekzakte vertikale. Por unu momento tie la suno lumigis ĝis la grundo de la vilaĝa puto. En Aleksandrio, 800 km pli norde, li mezuris la angulon de la sunradioj kiel 1/50 de tuta cirklo devianta de la vertikala, kio estas 7,2 gradoj. Se 1/50 de cirklo estas 800 km, la tuta cirklo, do la ĉirkaŭmezuro de la Tero estas 50 foje 800 = 40 000 km. Li mezuris kaj raportis per la tiam kutima mezurunuo "stadio".
Pliaj desegnoj pri la metodo troviĝas en la ekstera ligilo menciita sube. En ĝi fig.3 donas la plej bonan klarigon. La angulon α (7,2 gradoj) li povis mezuri per instrumento, sed pli simple li povis kalkuli ĝin, se li mezuris la altecon de alta domo kaj la distancon de ties ombro de la vertikala muro sur la grundo.
Komento pri la maldekstra bildo: en ĝi bedaŭrinde ne estas klare indikita, ke inter la punktoj 1 kaj 2 estas la sama angulo α = 7,2 gradoj.
Precizo kaj bazoj
Lia kalkulo estis tre preciza, malpli ol 10% neekzakta. Tiutempe anguloj ne povis esti mezuritaj tre ekzakte, kaj ankaŭ la distanco inter Syene kaj Aleksandrio certe ne estis konata tre ekzakte.
La kalkulo baziĝas sur du supozoj:
Mezurilo kaj rezulto
La unusola fonto pri la metodo de Eratosteno, Kleomedo, atestas, ke Eratosteno uzis iuspecan sunhorloĝon kiel mezurilon. Ĝia bazo havis la formon de kapsulo, kaj ĝia montrilo (gnomono ) staris vertikale. En la kapsulo estis skalo, tiel Eratosteno tagmeze dum somera solstico mezuris la ombran angulon formiĝantan ĉe la pinto de la gnomono. Ke je la sama tempo la suno super Syene staras vertikale, estis ĝenerale konate. Eratosteno do nur mezuris la ombran angulon en Aleksandrio.
Laŭ indiko de Kleomedes la rezulto estis, ke la ĉirkaŭmezuro de la tero egalas al 250 000 stadioj. Bedaŭrinde ne klaras, kiun stadion Kleomedes uzis: Ekzistis diversaj stadioj; la egalvaloroj en metroj varias de 177,6 m ĝis 192,3 m. Tio signifas, ke laŭ la mezurmetodo de Eratosteno la ĉirkaŭmezuro de la tero varias inter 44 250 kaj 48 075 km. La reala ĉirkaŭmezuro de la tero (laŭ meridiano) estas 40 008 km. Do la diferenco estas ja konsiderinda, sed tre malnete la rezulto de Eratosteno estas tamen trafa.
La scio de Kolumbo
1700 jarojn pli poste, kiam Kolumbo planis vojaĝi al Hindio per la okcidenta vojo, gravis scii, kiom longa estas la distanco. Laŭ la raportoj li supozis ege tro mallongan distancon. Ŝajnas, ke oni tute forgesis la metodon de Eratosteno. Fakte la distanco de Eŭropo al Hindio estas ĉirkaŭ kvarfoje pli longa ol tiu al Ameriko.
Sed efike tiu nescio favoris lian vojaĝon. Se li estus sciinta, ke la distanco estas tiom longa, li certe ne estus kuraĝinta vojaĝi. Kaj la hispana reĝino ne estus kuraĝinta riski la financadon de la vojaĝo.
Vidu ankaŭ
- Matematika algoritmo :Kribrilo de Eratosteno
Eksteraj ligiloj
En tiu vidu bildon 3, en kiu la angulo α estas klare videbla.
Referencoj
- ↑ Dictionnaire universel d'histoire et de géographie (Bouillet et Chassang)