Graikaĵoj de E₁ (supra) kaj Ei (malsupra)

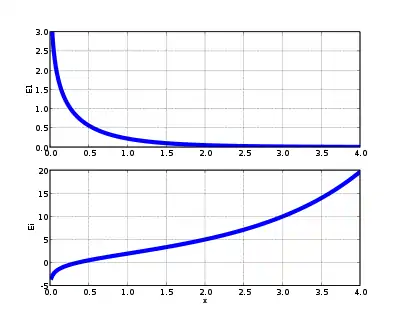
En matematiko, la integrala eksponenta funkcio Ei(x) estas difinita kiel difinta integralo de certa esprimo kun la eksponenta funkcio:

${\displaystyle {\mbox{Ei}}(x)=-\int _{-x}^{\infty }{\frac {e^{-t}}{t}}\,\mathrm {d} t}$

Ĉar integralo de 1/t malkonverĝas je t=0, la pli supre donita integralo estas komprenata kiel la koŝia ĉefa valoro.

La integrala eksponenta funkcio havas la serian prezenton:

${\displaystyle {\mbox{Ei}}(x)=\gamma +\ln x+\sum _{k=1}^{\infty }{\frac {x^{k}}{k\;k!}}\,}$

kie γ estas la eŭlera γ konstanto.

La eksponenta funkcia integralo estas proksime rilatanta al la logaritma integrala funkcio li(x)

li(x) = Ei (ln (x)) por ĉiu pozitiva reela x≠1.

Ankaŭ proksime rilatanta estas funkcio kiu integralatas super malsama limigo:

${\displaystyle {\rm {E}}_{1}(x)=\int _{x}^{\infty }{\frac {e^{-t}}{t}}\,\mathrm {d} t}$

Ĉi tiu funkcio povas esti estimita kiel etendado de la integrala eksponenta funkcio al negativaj reelaj nombroj per

Ei(-x) = - E₁(x)

Oni povas esprimi ilin ambaŭ per la tuta funkcio

${\displaystyle {\rm {Ein}}(x)=\int _{0}^{x}(1-e^{-t})\,{\frac {\mathrm {d} t}{t}}=\sum _{k=1}^{\infty }{\frac {(-1)^{k+1}x^{k}}{k\;k!}}}$

Uzante ĉi tiun funkcion, oni tiam povas difini, uzante la logaritmon

${\displaystyle {\rm {E}}_{1}(x)\,=\,-\gamma -\ln x+{\rm {Ein}}(x)}$

kaj

${\displaystyle {\rm {Ei}}(x)\,=\,\gamma +\ln x-{\rm {Ein}}(-x)}$

La integrala eksponenta funkcio povas ankaŭ esti ĝeneraligita al

${\displaystyle E_{n}(x)=\int _{1}^{\infty }{\frac {e^{-xt}}{t^{n}}}\,\mathrm {d} t}$

Eksteraj ligiloj

• Milton Abramowitz kaj Irene A. Stegun, Gvidlibro de matematikaj funkcioj kun formuloj, grafikaĵoj kaj matematikaj tabeloj. Novjorko, Dover, 1972. (Vidu en ĉapitro 5)
• Eric W. Weisstein, Integrala eksponenta funkcio en MathWorld.
• Eric W. Weisstein, En-funkcio en MathWorld.
• Formuloj por Ei