Duuma arbo

En la scienco pri komputado, la duuma arbo, aŭ binara arbo, estas arba datumstrukturo, en kiu ĉiuj verticoj havas maksimume po du infanojn. Ofte la du infanaj verticoj estas nomataj maldekstra kaj dekstra. Duumaj arboj estas uzataj en multaj informatikaj aplikaĵoj, inkluzive duuman serĉarbon kaj duuman piramidon.

Simpla duuma arbo kun grandeco 9 kaj profundeco 3. La vertico en la radiko havas la valoron 2

Bazaj difinoj

Po unu direkta eĝo konektas la generintan verticon (t.e., la vertico el kiu la eĝo eliras) kun siaj infanoj (t.e., la verticoj en kiujn la eĝoj eniras).

Verticoj sen infanoj nomiĝas folioj.
La vertico sen generintoj estas la radiko (ĉiu arbo havas po unu radikon).

La profundeco de vertico $v$ estas la nombro de eĝoj kiun oni devas sekvi komence de la radiko de la arbo por atingi la verticon $v$ . Unu nivelo de arbo inkluzivas ĉiujn verticojn havante la saman profundecon. La nivelo de la radiko estas la nivelo nulo laŭdifine.

La profundeco aŭ alteco de arbo estas la nombro de eĝoj inter la radiko kaj la plej profunda folio, t.e., la plej alta numero de nivelo.

Verticoj, kiuj havas komunan generinton, nomiĝas gefratoj.

Se ekzistas direkta vojo de vertico $p$ al vertico $q$ , tiam $p$ estas praulo de $q$ kaj $q$ estas posteulo de $p$ .

La grandeco de vertico estas la nombro de posteuloj, kiujn ĝi havas, inkluzive ĝi mem. Folioj ĉiam havas grandecon 1.

Tipoj de duumaj arboj

En plena duuma arbo ĉiuj verticoj havas aŭ nulo aŭ du infanojn.

Perfekta duuma arbo (fojfoje nomita kompleta duuma arbo) estas plena duuma arbo, en kiu ĉiuj folioj (verticoj kun nul infanoj) estas je la sama profundeco (distanco de la radiko).

Duon-perfekta duuma arbo estas arbo, en kiu ĉiu dekstra infano havas ĉiam maldekstran fraton. Por maldekstra infano ne certe estas dekstra frato.

Difino en grafeteorio

En grafeteorio, duuma arbo estas koneksa sencikla grafeo tia, ke la grado (nombro de eĝoj) de ĉiu vertico estas ne pli ol 3. Oni povas pruvi, ke en ĉiu duuma arbo estas ekzakte du pli da verticoj de grado unu ol estas de grado tri, sed povas esti iu ajn nombro de verticoj de grado du. Radikhava duuma arbo estas tia grafeo, kie unu el ĝiaj verticoj de grado ne pli ol 2 estas elektita kiel la radiko.

Kun la radiko tiel elektita, ĉiu vertico havos unikan difinitan generinton kaj ĝis du infanojn; tamen estas nesufiĉe da informoj por distingi inter maldekstra kaj dekstra infano. Se oni rezignas la postulon pri konekteco, t.e., se oni permesas ke en la grafeo troviĝu malsamaj konektitaj komponantoj, oni diras ke la strukturon estas arbaro (aro da malsamaj arboj).

Alternativa difino de duuma arbo uzas rekursian difinon pri orientataj grafeoj. Duuma arbo estas:

Sola vertico, aŭ
Unu vertico havante kiel infanoj du duumajn arbojn kun la sama profundeco.

Etendita duuma arbo difiniĝas jene rekursie:

Malplena aro estas unu etendita duuma arbo
Se T₁ kaj T₂ estas etenditaj duumaj arboj, krei novan verticon kaj fari ĝian maldekstra infano T1 kaj dekstra T2 se ili ne estas malplena. La rezulto estas unu etendita duuma arbo.

Manieroj por prezenti duumajn arbojn

Duumaj arboj povas esti konstruita de programlingvo en pluraj manieroj. En lingvo kun rikordoj kaj referencoj, duumaj arboj estas tipe konstruita tiel, ke oni faras arban vertican strukturon, kie ĉiu vertico enhavas iujn datumojn kaj referencojn al ĝia maldekstra kaj dekstra infano. Foje ĝi ankaŭ havas referencon al ĝia unika generinto. Se vertico havas malpli ol du infanojn, kelkaj de la infanaj referencoj povas havi specialan nulan valoron, aŭ ili povas referenci al speciala garda vertico.

Duumaj arboj povas ankaŭ esti prezentataj per tabeloj, kaj se la arbo estas plena, tiu-maniere oni ne malŝparas spacon. En tiu ĉi kompakta aranĝo, la radiko havas indekson $0$ , kaj la sekvaj verticoj havas indekson $i>0$ . La infanoj de vertico kun indekso $i$ troviĝas ĉe indeksoj $2i+1$ kaj $2i+2$ (se ĝi havas infanojn), dum ĝia generinto troviĝas je indekso $\left\lfloor {\frac {i-1}{2}}\right\rfloor$ . Ĉi tiu aranĝo estas sufiĉe simpla kaj la verticoj estas facile troveblaj, precipe dum antaŭorda vizito de la arbo. Aliflanke ĝi postulas seninterrompan parton da memoro, estas multekosta por ĝi kreski, kaj po arbo kun alteco $h$ kaj $n$ verticojn malŝparas memorspacon proporcie al $2^{h}-n$ .

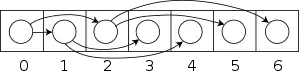
Malgranda plena duuma arbo registrita en tabelo

Trairi duumajn arbojn

Ofte oni deziras viziti ĉiujn verticojn en arbo po unufoje kaj analizi la datumojn tie entenataj. Pluraj ordinaraj metodoj ekzistas, per kiu oni povas viziti la verticojn, kaj ĉiuj el ili sekvas malsamajn principojn.

Antaŭ-orda, en-orda kaj post-orda trairo

Antaŭ-orda, en-orda kaj post-orda trairo vizitas ĉiun verticon en arbo per rekursia algoritmo. Se la radika vertico estas vizitita antaŭ ĝia subarboj, ĉi tiu estu nomata ĉi tie antaŭ-orda trairo; se poste, tiam post-orda; se inter ambaŭ, tiam en-orda trairo. En-orda trairo estas utila en duumaj serĉaj arboj, kie ĉi tiu trairo vizitas la verticojn en pligrandiĝanta ordo.

Vizito laŭ profundeco

En profunden-unue-ordo la algoritmo ne vizitas la arbon nivelon post nivelo, sed ĉiam procedas kiel eble plej longe for de la radiko, atingante la plej profundajn verticojn. La jam-menciitaj antaŭ-orda, en-orda kaj post-orda trairoj estas ĉiuj specialaj kazoj de tiu ĉi vizit-maniero.

Vizito laŭ niveloj

En la vizito laŭ niveloj, la algoritmo vizitas unue la radikon, poste ĉiujn verticojn ĉe nivelo 1, poste ĉiujn verticojn ĉe nivelo 2, ktp, ĝis la algoritmo atingas la lastan nivelon (t.e., la plej profundan).

Enkodigoj (kodoprezentoj)

Koncizaj kodoprezentoj

Konciza datumstrukturo estas iu, kiu prenas kiel eble plej malmulte da spaco. La nombro de malsamaj duumaj arboj de $n$ verticoj estas $\mathrm {C} _{n}$ , la $n$ -a Katalana nombro (alprenanta, ke ni vidas arbojn kun identa strukturo kiel identaj). Por granda $n$ , tiu ĉi estas pli-malpli $4^{n}$ ; tial ni bezonas almenaŭ pli-malpli $\log _{2}4^{n}=2n$ bitojn por enkodi. Konciza duuma arbo pro tio devus okupi nur 2 bitojn je vertico.

Unu simpla reprezento, kiu atingas tiun ĉi limo, estas viziti la verticojn de la arbo en antaŭa ordo, eliganta "1" por interna vertico kaj "0" por folio. Se la arbo enhavas datumojn , ni povas simple samtempe registri ĝin en najbara tabelo en antaŭordo. La sekva funkcio faras tion:

function EnkodiguKoncize(vertico n, bitĉeno strukturo, tabelo datumoj) {
    if n = nil then
        aldonu 0 al strukturo;
    else
        aldonu 1 al strukturo;
        aldonu n.datumoj al datumoj;
        EnkodiguKoncize(n.maldekstra, strukturo, datumoj);
        EnkodiguKoncize(n.dekstra, strukturo, datumoj);
}

Finfine la bitĉeno strukturo havas nur $2n+1$ , kie $n$ estas la nombro de internaj verticoj; ni eĉ ne devas registri ĝian longon. Por montri, ke neniu informo estas perdita, ni povas konverti la rezulton al la originala arbo tiel ĉi:

function ElkodiguKoncize(bitĉeno strukturo, tabelo datumoj) {
    forprenu unuan biton de strukturo kaj metu ĝin en b
    if b = 1 then
        kreu novan verticon n
        forprenu unuan elementon kaj metu ĝin en n.datumoj
        n.maldekstra = ElkodiguKoncize(strukturo, datumoj)
        n.dekstra = ElkodiguKoncize(strukturo, datumoj)
        return n
    else
        return nil
}

Pli malnaiva koncizaj prezentoj permesas ne nur kompaktan registradon de arboj, sed eĉ utilaj operacioj sur tiuj arboj rekte, dum ili estas ankoraŭ en ilia konciza formo.

Enkodigi n-umaj arboj kiel duumaj arboj

Estas bijekcio (unu-al-unu-mapo) inter ĝenerale ordaj arboj kaj duumaj arboj, kiu precipe estas uzitaj de Lisp, por prezenti ĝeneralajn ordajn arbojn kiel duumaj arboj. Ĉiu vertico N en la orda arbo korespondas al vertico N' en la duuma arbo; la maldekstra infano de N' estas la vertico korespondanta al la unua infano de N, kaj la dekstra infano de N' estas la vertico korespondanta al la venonta frato de N --- tio estas, la venonta vertico en ordo inter la infanoj de la gepatro de N.

Unu maniero percepti tion ĉi estas, ke ĉiuj verticaj infanoj estas en ligillisto, ĉenitaj kun iliaj dekstra kampo, kaj la vertico havas nur referencon al la komenco aŭ kapo de tiu ĉi listo, tra ĝia maldekstra kampo.

Ekzemple en la arbo maldekstren, A havas la 6 infanojn {B,C,D,E,F,G}. Ĝi povas esti konvertita al la duuma arbo dekstren.

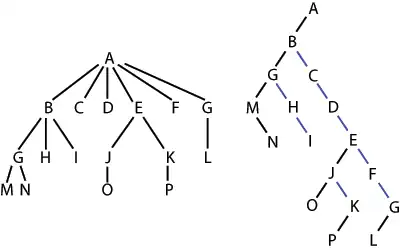
Ekzemplo de konvertanta n-uma arbo al duuma arbo

Oni povas pensi pri la duuma arbo kiel la originala arbo kuŝigita, kun la nigraj maldekstraj eĝoj prezentantaj unua infano kaj la bluaj dekstraj eĝoj prezentantaj venonta gefrato. La folioj de la arbo maldekstre oni skribus en Lisp kiel:

(((M N) H I) C D ((O) (P)) F (L))

kiu estus realigita en memoro kiel la duuma arbo dekstre, sen literoj sur tiuj verticoj, kiuj havas maldekstran infanon.

Referencoj

Donald Knuth. The art of computer programming vol 1. Fundamental Algorithms, Third Edition. Addison-Wesley, 1997. ISBN 0-201-89683-4. Section 2.3, especially subsections 2.3.1–2.3.2 (pp.318–348).
Kenneth A Berman, Jerome L Paul. Algorithms: Parallel, Sequential and Distributed. Course Technology, 2005. ISBN 0-534-42057-5. Chapter 4. (pp.113–166).

Vidu ankaŭ

B-arbo
Duuma spaca dispartigado
rekursio

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.