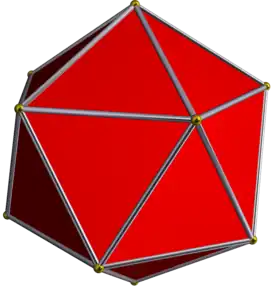
Dudekedro
Klaku por rigardi turnantan bildon
Speco	Regula pluredro Trianguledra pluredro
Vertica figuro	3.3.3.3.3
Bildo de vertico
Bildo de reto
Simbolo de Wythoff	5 | 2 3
Simbolo de Schläfli	{3,5} kaj ${\displaystyle s{\begin{Bmatrix}3\\3\end{Bmatrix}}}$
Figuro de Coxeter-Dynkin
Indeksoj	U22 C25 W4
Simbolo de Bowers	Ike
Verticoj	12
Lateroj	30
Edroj	20
Edroj detale	20{3}
χ	2
Geometria simetria grupo	Ih
Duedra angulo	138,189685°
Duala	Dekduedro
Bildo de duala

Dudekedro estas ĉiu pluredro havanta 20 edrojn, sed kutime estas subkomprenata regula dudekedro, kiu havas egallaterajn triangulojn kiel edroj.

La regula dudekedro estas unu el la kvin platonaj solidoj. Ĝi estas konveksa regula pluredro komponita el 20 triangulaj edroj, kaj kvin edroj kuniĝas je ĉiu el verticoj. Ĝi havas 30 laterojn kaj 12 verticojn. Ĝia duala pluredro estas la dekduedro.

Formuloj

Se la randa longo de regula dudekedro estas a, la radiuso de ĉirkaŭskribita sfero estas

${\displaystyle r_{u}={\frac {a}{2}}{\sqrt {\varphi {\sqrt {5}}}}={\frac {a}{4}}{\sqrt {10+2{\sqrt {5}}}}\approx 0,9510565163\cdot a}$

La radiuso de enskribita sfero (tangenta al ĉiu de la dudekedraj edroj) estas

${\displaystyle r_{i}={\frac {\varphi ^{2}a}{2{\sqrt {3}}}}={\frac {a}{12}}{\sqrt {3}}\left(3+{\sqrt {5}}\right)\approx 0,7557613141\cdot a}$

La radiuso de sfero kiu tuŝas ĉiujn laterojn (je la mezo de la lateroj) estas

${\displaystyle r_{m}={\frac {a\varphi }{2}}={\frac {1}{4}}\left(1+{\sqrt {5}}\right)a\approx 0,80901699\cdot a}$

kie ${\displaystyle \varphi }$ (ankaŭ nomata kiel ${\displaystyle \tau }$) estas la ora proporcio.

La surfaca areo A estas:

${\displaystyle A=5{\sqrt {3}}a^{2}\approx 8,66025404a^{2}}$

La volumeno V estas:

${\displaystyle V={\frac {5}{12}}(3+{\sqrt {5}})a^{3}\approx 2,18169499a^{3}}$

Karteziaj koordinatoj

Oraj ortanguloj en dudekedro

Karteziaj koordinatoj de verticoj de dudekedro centrita je la nulo de koordinatoj kun longo de lateroj 2:

${\displaystyle (0,\pm 1,\pm \varphi )}$

${\displaystyle (\pm 1,\pm \varphi ,0)}$

${\displaystyle (\pm \varphi ,0,\pm 1)}$

kie ${\displaystyle \varphi ={\tfrac {1+{\sqrt {5}}}{2}}}$ refoje estas la ora proporcio.

Geometriaj rilatoj

La tiuj verticoj formas kvin arojn ĉiu el tri reciproke perpendikularaj oraj ortanguloj.

La 12 randoj de okedro povas esti disdividita en la ora proporcio tiel ke la rezultantaj verticoj donas regulan dudekedron. La kvin okedroj donantaj dudekedro formas regulan pluredran kombinaĵon.

Dudekedro kiel riproĉa kvaredro

Estas malformiĝoj de la dudekedro kiuj estas ne regulaj sed vertico-unuformoj. Ili estas invariantaj sub la samaj turnadoj kiel la kvaredro.

La dudekedro havas grandan kvanton de steligoj, inkluzivanta unuon el pluredroj de Keplero-Poinsot.

La dudekedro estas unika inter la platonaj solidoj pro havo de duedra angulo ne malpli ol 120°. Ĝia duedra angulo estas proksimume 138,19°. Seslateroj havantaj angulojn ne malpli ol 120° ne povas esti uzataj kiel edroj de konveksa regula pluredro ĉar ĉi tia konstruado bezonas ke almenaŭ tri edroj devas kuniĝi je vertico kaj post ĉi tio devas resti pozitiva angula difekto por faldado en tri dimensioj. Simile, dudekedroj ne povas esti uzataj kiel ĉeloj de konveksa regula plurĉelo ĉar almenaŭ tri ĉeloj devas kuniĝi je latero kaj same devas esti pozitiva angula difekto por faldado en kvar dimensioj (ĝenerale por konveksa hiperpluredro en n dimensioj, almenaŭ tri facetoj devas kuniĝi je n-3 dimensia rando kaj ili devas lasi pozitivan angulan difekton por faldado en n-spaco).

Tamen, en kombino kun taŭgaj ĉeloj havantaj pli malgrandajn duedrajn angulojn, dudekedroj povas esti uzataj kiel ĉeloj en duonregulaj plurĉeloj (ekzemple en la riproĉa 24-ĉelo), same kiel seslateroj povas esti uzataj kiel edroj en duonregulaj pluredroj (ekzemple en la senpintigita dudekedro). Nekonveksaj hiperpluredroj ne havas ĉi tiujn limigojn pri la anguloj kiel konveksaj hiperpluredroj, kaj do dudekedroj estas la ĉeloj de la dudekedra 120-ĉelo, unu el la dek nekonveksaj regulaj plurĉeloj.

Kvinlatera kontraŭprismo - la meza parto de la dudekedro

Dudekedro povas ankaŭ nomiĝi kiel turnoplilongigita kvinlatera dupiramido. Ĝi povas esti malkomponita enen de turnoplilongigita kvinlatera piramido kaj kvinlatera piramido aŭ en kvinlateran kontraŭprismon kaj du egalajn kvinlaterajn piramidojn.

La dudekedron oni povas nomi ankaŭ kiel riproĉa kvaredro, aŭ kiel riproĉa okedro (ĉar okedro estas rektigita kvaredro).

Solidoj de Johnson

Solidoj de Johnson surbaze de la dudekedro estas:

Turnoplilongigita kvinlatera piramido (J11) (malkreskigita dudekedro)	Najbarodumalkreskigita dudekedro (J62)	Trimalkreskigita dudekedro (J63)	Pligrandigita trimalkreskigita dudekedro (J64)

Vico de rilatantaj pluredroj kaj kahelaroj

La dudekedro estas riproĉa kvaredro kaj estas ero de vico de riproĉigitaj regulaj pluredroj kaj regulaj kahelaroj de la eŭklida kaj hiperbola ebenoj kun verticaj figuroj (3.3.3.3.n).

Dudekedro (3.3.3.3.3)	Riproĉa kubo (3.3.3.3.4)	Riproĉa dekduedro (3.3.3.3.5)
Riproĉa seslatera kahelaro 3.3.3.3.6	Riproĉa ordo-3 seplatera kahelaro (3.3.3.3.7)	Riproĉa ordo-3 oklatera kahelaro (3.3.3.3.8)

Unuformaj pluredraj kombinaĵoj

Kombinaĵo de 2 dudekedroj

Kombinaĵo de 5 dudekedroj

Uzo

• Multaj virusoj, ekzemple herpeto, havas formon de dudekedro. Por vivaj strukturoj kiuj estas konstruita el ripetitaj identaj proteinaj aĵoj la dudekedro estas la plej facila formo.
• La regula dekduedro estas ofte uzita en rolludoj kiel 20-flankita ĵetpluredro ("d20" mallonge). Ankaŭ povas esti ke cifero "0" ... "9" estas markitaj po dufoje, tiam ĝi estas d10.

Diversaĵoj

Se ĉiu rando de dudekedro estas anstataŭigita per 1 oma rezistancilo, la rezistanco inter kontraŭaj verticoj estas 0,5 omoj, kaj tiu inter najbaraj verticoj 11/30 omoj^[1]

Vidu ankaŭ

• Senpintigita dudekedro
• Dudekedro–seslateraj kradoj en vetera antaŭdiro
• Kombinaĵo de dekduedro kaj dudekedro

Referencoj

Eksteraj ligiloj

• Eric W. Weisstein, Dudekedro en MathWorld.
• La unuformaj pluredroj
• Virtualaj realaj pluredroj