Matematika funkcio estas disĵeto (aŭ, paŭsante internacie rekoneblan gentalingvan formon, injekcio, enĵeto aŭ eĉ enjekcio), se ĝi atingas ĉiun valoron maksimume solfoje. Tio signifas, ke neniu elemento en ĝia bildaro (valoraro) estas bildo (valoro) de pli ol unu argumento. Alivorte, disaj argumentoj havas disajn bildojn (neniuj «kungluiĝas»).

Disĵeta funkcio ne nepre estas ĉie difinita.

Formala difino

Estu ${\displaystyle X}$ kaj ${\displaystyle Y}$ aroj, kaj ${\displaystyle f:X\to Y}$ funkcio de ${\displaystyle X}$ al ${\displaystyle Y}$.

${\displaystyle f}$ estas disĵeto, se por ĉiu ${\displaystyle y}$ el ${\displaystyle Y}$ ekzistas ne pli ol unu tia ${\displaystyle x}$ el ${\displaystyle X}$ ke ${\displaystyle f(x)=y}$.

${\displaystyle \forall _{x_{1},x_{2}\in X}\;x_{1}\neq x_{2}\implies f(x_{1})\neq f(x_{2})}$.

Ekvivalenta difino

${\displaystyle f}$ nomiĝas disĵeto, se por ĉiuj ${\displaystyle x_{1}}$, ${\displaystyle x_{2}}$ el ${\displaystyle X}$ kaj ${\displaystyle y}$ el ${\displaystyle Y}$ validas: se ${\displaystyle f(x_{1})=y}$ kaj ${\displaystyle f(x_{2})=y}$, tiam ${\displaystyle x_{1}=x_{2}}$.

${\displaystyle \forall _{x_{1},x_{2}\in X}\;f(x_{1})=f(x_{2})\implies x_{1}=x_{2}}$.

• 
  Funkcio disĵeta (sed ne surĵeta).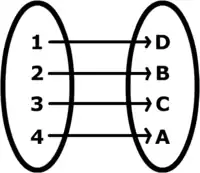
• 
  Funkcio disĵeta kaj surĵeta (dissurĵeto).
• 
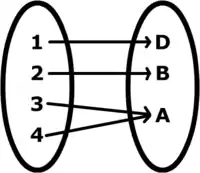  Ne-disĵeta (aŭ «kunĵeta») funkcio.

Lingva noto pri «enĵeto» kaj «enjekcio»

Ekzemplo pri «ĵeto en»

Ĉar surĵeto (aŭ «surjekcio») estas «ĵeto sur la tutan celan aron», tial la normala lingva logiko postulas, ke enĵeto estu «ĵeto en la celan aron» (t.e. tia «ĵeto», kiu ne estas «surĵeto»). Tamen iuj matematikistoj, meĥanike paŭsante la malracian internacian terminon injection, uzas la vorton «enĵeto» por la signifo «disĵeto», la signifo kiu neniel ajn sekvas el «en» + «ĵeto». Tio estas ne nur tute malracia, sed ankaŭ altgrade misgvida kaj nepre evitinda. Se oni ial malvolas uzi la klaran esperantan prefikson dis- kaj preferas neanalizindan terminon internacian, oni prefere diru injekcio (samkiel oni diras projekcio), sen traduki la misgvidan in-, same kiel okaze de injekto, kiu ja ne estu "enjekto".

Vidu ankaŭ

• Surĵeto
• Dissurĵeto
• Vikipedio:Projekto_matematiko/Disĵeta_funkcio
• «disĵeto» en la «Komputada leksikono».