En kombinatoriko, cikla permuto estas permuto en cikla ordo.

La nocio estas uzata kun malsamaj, sed similaj sencoj:

Varianto 1

Permuto P super aro S kun k eroj estas cikla permuto kun kompenso t se kaj nur se

la eroj de S povas esti entute ordigitaj, (c[1] < c[2] < ... < c[k]) kaj la surĵeto de P povas esti skribita kiel:

P(c[i]) = c[i+t] por i = 1, 2, ..., k-t, kaj

P(c[i]) = c[i+t-k] por i = k-t+1, ..., k.

Ĉiu ĉi tia cikla permuto estas konstruita el akurate PGKD (k, t) disaj cikloj. En ĉiu ciklo la eroj estas permutataj nur inter si. Vidu en cikloj kaj fiksaj punktoj.

Ĉi tiaj ciklaj permutoj estas nomataj ankaŭ kiel turnadoj.

Ekzemplo kun k=8, t=2:

${\displaystyle {\begin{pmatrix}1&2&3&4&5&7&6&8\\3&4&5&7&6&8&1&2\end{pmatrix}}}$

Ĝi konsistas el PGKD(8, 2) = 2 cikloj. La unua ciklo konsistas el eroj 1, 3, 5, 6, la dua ciklo konsistas el eroj 2, 4, 7, 8.

Varianto 2

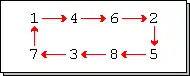Permuto estas cikla permuto se kaj nur se ĝi konsistas el akurate unu ciklo.

Ĉiu permuto super aro de k eroj estas cikla permuto de varianto 2 se kaj nur se ekzistas tia ordigo super la aro ke la permuto estas cikla permuto de varianto 1 kun PGKD(k, t) = 1.

Ekzemplo:

${\displaystyle {\begin{pmatrix}1&2&3&4&5&7&6&8\\4&5&7&6&8&1&2&3\end{pmatrix}}={\begin{pmatrix}1&4&6&2&5&8&3&7\\4&6&2&5&8&3&7&1\end{pmatrix}}}$

Varianto 3

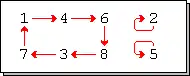Permuto estas cikla permuto se kaj nur se nur unu el cikloj el kiuj ĝi konsistas havas longon pli grandan ol 1.

Ĉiu cikla permuto de varianto 3 estas unio de cikla permuto de varianto 2 kaj iu kvanto da fiksaj punktoj.

Ĉiu cikla permuto de varianto 2 estas ankaŭ cikla permuto de varianto 3 kun nula kvanto da fiksaj punktoj.

Ekzemplo:

${\displaystyle {\begin{pmatrix}1&4&6&8&3&7&2&5\\4&6&8&3&7&1&2&5\end{pmatrix}}}$

Vidu ankaŭ

• Cikla skribmaniero
• Nombro de Stirling
• Cezara ĉifro