Cikla grafeo
Plia nomo Simpla cikla grafeo
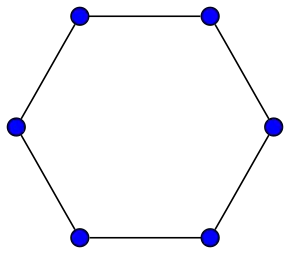Bildo
Cikla grafeo de 6 verticoj
hamiltona grafo • regula grafo • Vertico-transitiva grafeo • edge-transitive graph • unueĝlonga grafo • koneksa grafo • eŭlera ciklo • ebena grafo
Verticoj n
Lateroj n
Aŭtomorfioj 2n
Koloriga nombro 3 se n estas nepara,
2 se n estas para
Propraĵoj 2-regula,
vertico-transitiva,
latero-transitiva,
unua distanca

En grafeteorio, cikla grafeo aŭ simpla cikla grafeo estas grafeo kiu konsistas de sola vojo (ciklo). En aliaj vortoj, iu kvanto da verticoj estas koneksa kiel fermita ĉeno. La cikla grafeo kun n verticoj estas skribata kiel Cn. La kvanto de lateroj en Cn egalas al kvanto de verticoj n. Ĉiu vertico havas gradon 2; tio estas, ĉiu vertico havas akurate du laterojn koneksajn al ĝi.

Ciklo kun para kvanto de verticoj estas nomata kiel para ciklo; ciklo kun nepara kvanto de verticoj estas nomata kiel nepara ciklo.

Propraĵoj

Cikla grafeo estas:

  • Koneksa grafeo
  • 2-regula grafeo
  • Eŭlera grafeo
  • Grafeo de Hamilton
  • 2-vertice kolorigebla, se kaj nur se ĝi havas paran kvanton de verticoj. Pli ĝenerale, grafeo estas 2-vertice kolorigebla se kaj nur se ĝi ne enhavas neparajn ciklojn.
  • 2-latere kolorigebla se kaj nur se ĝi havas paran kvanton de verticoj
  • 3-vertice kolorigebla kaj 3-latere kolorigebla, por ĉiu kvanto de verticoj
  • Unua distanca grafeo

Ĉar cikla grafeo povas esti desegnita kiel regula plurlatero, la aŭtomorfia grupo (simetrioj) de n-ciklo estas la samaj kiel tiuj de regula plurlatero kun n lateroj, la duedra grupo de ordo 2n. Aparte, tie ekzistas simetrioj metantaj ĉiun unu donitan verticon al ĉiu la alia donita vertico, kaj ĉiun unu donitan lateron al ĉiu la alia donita latero, tiel la n-ciklo estas simetria grafeo.

Direktita cikla grafeo

Direktita cikla grafeo de longo 8

Direktita cikla grafeo estas direktita versio de cikla grafeo, kun ĉiuj lateroj orientitaj en la sama direkto.

En orientita grafeo, subaro de lateroj kiu enhavas almenaŭ unu lateron (arkon) de ĉiu direktita ciklo estas nomata kiel retrokupla arka aro. Simile, subaro de verticoj kiu enhavas almenaŭ unu verticon de ĉiu direktita ciklo estas nomata kiel retrokupla vertica aro.

En direktita cikla grafeo ĉiu vertico havas eneniran duongradon 1 kaj eliran duongradon 1.

Direktitaj ciklaj grafeoj estas grafeoj de Cayley por ciklaj grupoj.

Vidu ankaŭ

Eksteraj ligiloj

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.