Matematika funkcio nomiĝas dissurĵeto, se ĝi estas kaj disĵeto, kaj surĵeto.

Ĉie difinita dissurĵeto (priskribebla ankaŭ kiel reciproke unuvalora rilato) nomiĝas bijekcio aŭ inversigebla funkcio. La karakterizon inversigebla pravigas tio, ke la inverso de ĉie difinita dissurĵeta funkcio (konsiderata kiel duvalenta rilato) estas duvalenta funkcia rilato (kiu mem estas ĉie difinita dissurĵeta funkcio).

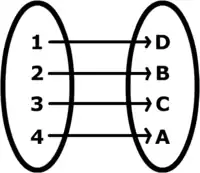
Bijekcio

Formala difino

Oni povas difini dissurĵetan funkcion kaj bijekcion ankaŭ rekte, sen mencii la nociojn disĵeto kaj surĵeto:

Estu ${\displaystyle f}$ funkcio ("ĵeto") de ${\displaystyle X}$ al ${\displaystyle Y}$, t.e. ${\displaystyle f:X\to Y}$.

${\displaystyle f}$ estas dissurĵeto, se por ĉiu ${\displaystyle y}$ el ${\displaystyle Y}$ ekzistas unu kaj nur unu tia ${\displaystyle x}$ el ${\displaystyle X}$, ke ${\displaystyle f(x)=y}$.

${\displaystyle f}$ estas bijekcio aŭ inversigebla funkcio, se por ĉiu ${\displaystyle x}$ el ${\displaystyle X}$ ekzistas unu kaj nur unu ${\displaystyle y}$ el ${\displaystyle Y}$ tia, ke ${\displaystyle f(x)=y}$ kaj por ĉiu ${\displaystyle y}$ el ${\displaystyle Y}$ ekzistas tia ${\displaystyle x}$ el ${\displaystyle X}$, ke ${\displaystyle f(x)=y}$.

Vidu ankaŭ

• Disĵeto
• Surĵeto