Pri la aliaj signifoj de aro rigardu en Aro.
En matematiko, la nocio de aro estas unu el la plej fundamentaj nocioj. Aro estas kolekto da elementoj konsiderataj kiel unu tutaĵo. Aro povas esti malplena, sed ne povas enhavi plurajn ekzemplerojn de unu elemento.
La nocio de aro estas tiel fundamenta, ke kutime oni ne difinas ĝin matematike, sed uzas ĝin kiel bazon por difini aliajn matematikajn konceptojn.
Oni signas arojn per latinaj majuskloj: A, B, C, D, .. kaj ĝiajn elementojn per minuskloj: a, b, c, d, ... La fakton ke a prezentas elementon de A, simbole oni skribas kiel . (legu: a apartenas al A). La aro kies elementoj estas a, b, c, ... oni skribas jene: A={a; b; c; ...}, kaj la aro de tiuj elementoj, kiuj kontentigas ian P kondiĉon, oni skribas kiel {x ∈ A | P} aŭ {x ∈ A : P}. Ekzemple la aro de ĉiuj naturalaj nombroj kiuj estas malpli ol 100, signatas: , kie N estas la aro de naturaj nombroj.
- La aro, kiu enhavas neniajn elementojn, nomiĝas malplena aro kaj estas signata per la simbolo ø. Ekzemple, la aro de homoj loĝantaj en la suno estas malplena.
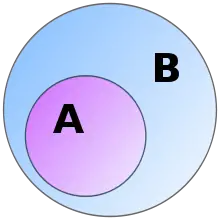
- La aro A nomiĝas subaro de B, se ĉiuj elementoj de A apartenas al B kaj skribas: A ⊂ B. Ekzemple, se la A prezentas la aron de ortanguloj, kaj B - la aron de paralelogramoj, tiam A ⊂ B.
- Se A ⊂ B kaj B ⊂ A, tiam la aroj A kaj B estas egalaj kaj oni skribas: A=B.
- La aro de ĉiuj elementoj de la aroj A kaj B, kiuj apartenas almenaŭ al unu el du nomitaj aroj, nomiĝas kunaĵo de du aroj kaj signatas kiel A ∪ B.
- La aro de ĉiuj tiuj elementoj de A kaj B, kiuj apartenas samtempe al ambaŭ aroj, estas nomata komunaĵo de la aroj kaj signatas kiel A ∩ B.
Ekzemple, se A={1;2;3;4;5} kaj B={1;3;5;7}, tiam A ∪ B = {1;2;3;4;5;7} kaj A ∩ B ={1;3;5}
- La aro de ĉiuj elementoj de la aro A, kiuj ne apartenas samtempe al la aro B, estas nomata diferenco aŭ diferencaro kaj signatas kiel
 |  |   |
Se estas donita la aroj A kaj B, kaj la regulo, per kiu ni povas kunigi iajn parojn (a; b), kie a ∈ A kaj b ∈ B, oni diras ke estas donita konformeco inter A kaj B, kaj b estas nomata konforma al a. Ekz. inter A={1,5,10,14,20} kaj B={2,3,7} oni povas establi konformon per tia regulo: "al elemento de A konformas ĝia divizoro el B". Ĉi tiu konformo donas sekvajn parojn: (10;2), (14;2), (14;7), (20;2). Inter la du donitaj aroj povas ekzisti ankaŭ inversa konformo.
La konformeco inter A kaj B estas unu-al-unua konformeco, se plenumiĝas la sekvaj du kondiĉoj:
- 1. al ĉiu a (a ∈ A) konformas la sola elemento el B;
- 2. ĉiu elemento el B estas konforma por la sola elemento el A.
Du aroj estas ekvivalentaj, se inter ili povas establi unu-al-unuan konformecon. Ekz. la aro de naturalaj nombroj {1;2;3;...} kaj la aro de paraj nombroj {2;4;6;...} estas ekvivalentaj, ĉar inter ili oni povas establi unu-al-unuan konformon laŭ regulo: "al ĉiu naturala nombro n konformu la paran nombron 2n".
La aroj povas esti ankaŭ finiaj (kun difinita nombro de elementoj) kaj nefiniaj (kun senfina nombro de elementoj).
Aro-teorio estas la bazo de moderna matematiko.
La aron de ĉiuj subaroj de aro A oni nomas la partaĵa aro de A.
La reta vortaro ( subaro Arkivigite je 2006-09-23 per la retarkivo Wayback Machine ) diras ke la aro de ĉiuj subaroj ne havas specialan nomon.