En geometrio arkimeda solido estas alte simetria duonregula vertico-transitiva konveksa pluredro komponita el du aŭ pli multaj specoj de regulaj plurlateroj. Arkimeda solido diferenciĝas de la platonaj solidoj kiuj estas komponita el nur unu speco de plurlatero, kaj de la solidoj de Johnson kiuj estas ne vertico-transitivaj.
Kiel arkimedaj solidoj ne estas konsiderataj pluredroj de la duedra simetrio - prismoj kaj kontraŭprismoj.
Laŭ sia difino ĉiuj arkimedaj solidoj estas unuformaj pluredroj.
Prismoj, kontraŭprismoj kaj arkimedaj solidoj estas la tuta aro de konveksaj duonregulaj pluredroj
Ĉiuj arkimedaj solidoj povas esti faritaj per konstruado de Wythoff.
Fonto de nomo
La arkimedaj solidoj prenas sian nomon de Arkimedo, kiu diskutis ilin en sia nun perdita verko. Dum la Renaskiĝo, artistoj kaj matematikistoj alte taksis purajn formojn kaj reesploris ĉi ĉiujn pluredrojn. Tiu serĉo estis plenumita ĉirkaŭ 1619 de Keplero, kiu difinis ankaŭ prismojn, kontraŭprismojn, kaj la ne-konveksajn solidojn konatajn kiel solidoj de Keplero-Poinsot.
Klasifiko
Estas 13 arkimedaj solidoj. Inter ili estas 2 nememspegulsimetriaj, ambaŭ simetriaj formoj de ĉiu el 2 nememspegulsimetriaj pluredroj estas kutime konsiderataj kiel la sama speco de pluredro. La vertica konfiguro priskribas la specojn de regulaj plurlateroj, kiuj kuniĝas iu ajn donita vertico. Ekzemple, vertica konfiguro (4,6,8) signifas ke kvadrato, seslatero kaj oklatero kuniĝas je vertico (kun la laŭhorloĝnadla ordo ĉirkaŭ la vertico).
La kvanto de verticoj estas 720° dividita per la vertica angula difekto.
| Nomo | Solido | Travidebla | Edroj | Lateroj | Verticoj | Vertica konfiguro | Simetria grupo | |
|---|---|---|---|---|---|---|---|---|
| Senpintigita kvaredro |  |
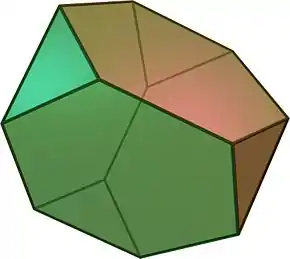 |
8 | 4 trianguloj 4 seslateroj | 18 | 12 | 3.6.6 | Td |
| Kubokedro |  |
 |
14 | 8 trianguloj 6 kvadratoj |
24 | 12 | 3.4.3.4 | Oh |
| Senpintigita kubo |  |
 |
14 | 8 trianguloj 6 oklateroj | 36 | 24 | 3.8.8 | Oh |
| Senpintigita okedro |  |
 |
14 | 6 kvadratoj 8 seslateroj | 36 | 24 | 4.6.6 | Oh |
| Rombokub-okedro (malgranda rombokub-okedro) |
 |
 |
26 | 8 trianguloj 18 kvadratoj | 48 | 24 | 3.4.4.4 | Oh |
| Senpintigita kubokedro (granda rombokub-okedro) |
 |
 |
26 | 12 kvadratoj 8 seslateroj 6 oklateroj |
72 | 48 | 4.6.8 | Oh |
| Riproĉa kubo (nememspegulsimetria) |
  |
 Mallaŭ horloĝa nadlo  Laŭ horloĝa nadlo |
38 | 32 trianguloj 6 kvadratoj | 60 | 24 | 3.3.3.3.4 | O |
| Dudek-dekduedro |  |
 |
32 | 20 trianguloj 12 kvinlateroj |
60 | 30 | 3.5.3.5 | Ih |
| Senpintigita dekduedro |  |
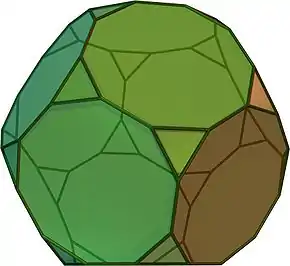 |
32 | 20 trianguloj 12 deklateroj | 90 | 60 | 3.10.10 | Ih |
| Senpintigita dudekedro |  |
 |
32 | 12 kvinlateroj 20 seslateroj | 90 | 60 | 5.6.6 | Ih |
| Rombo-dudek-dekduedro (malgranda rombo-dudek-dekduedro) |
 |
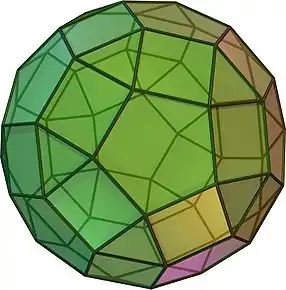 |
62 | 20 trianguloj 30 kvadratoj 12 kvinlateroj |
120 | 60 | 3.4.5.4 | Ih |
| Senpintigita dudek-dekduedro (granda rombo-dudek-dekduedro) |
 |
 |
62 | 30 kvadratoj 20 seslateroj 12 deklateroj |
180 | 120 | 4.6.10 | Ih |
| Riproĉa dekduedro (nememspegulsimetria) |
  |
 Mallaŭ horloĝa nadlo  Laŭ horloĝa nadlo |
92 | 80 trianguloj 12 kvinlateroj | 150 | 60 | 3.3.3.3.5 | I |
La kubokedro kaj dudek-dekduedro estas latero-unuformaj kaj do estas kvazaŭregulaj.
La dualaj pluredroj de la arkimedaj solidoj estas nomataj kiel la katalanaj solidoj. Ankaŭ la dupiramidoj kaj kajtopluredroj estas la edro-uniformaj solidoj kun regulaj verticoj.
Vidu ankaŭ
Referencoj
- Williams, Robert. (1979) The Geometrical Foundation of Natural Structure: A Source Book of Design - La Geometria Fundamento de Natura Strukturo: Fonta Libro de Dizajno. Dover Publications, Inc. ISBN 0-486-23729-X. (Sekcio 3-9)
Eksteraj ligiloj
- Eric W. Weisstein, Arkimeda solido en MathWorld.
- Paperaj modeloj de arkimedaj solidoj
- Libera papero modeloj (retoj) de Arkimedaj solidoj Arkivigite je 2007-02-20 per la retarkivo Wayback Machine
- La uniformaj pluredroj
- Virtualaj realaj pluredroj - la enciklopedio de pluredroj
- Antaŭlasta modula origamio
- Interagaj 3D pluredroj Arkivigite je 2005-04-03 per la retarkivo Wayback Machine en Javo