Estas tri kutimaj spacaj dimensioj: longo (aŭ profundo), larĝo, kaj alto, ofte skribataj kiel x, y kaj z (ne nepre respektive). x kaj y aksoj apera en ebeno. En la 3-a dimensio, z estas uzata.

La kvara dimensio estas ofte identigita kun tempo en fiziko, kaj kiel tia estas uzita al ekspliki la ne-Eŭklida spaco-tempo uzita en teorioj de speciala relativeco kaj fizika relativeco. Tempo ne estas tamen tute samrajta kun la 3 spacoj koordinatoj. Sed povas esti imagita ankaŭ la 4-a spaca koordinato, tiel ke ĉiuj 4 koordinatoj havas la samajn propraĵojn. Kaj tiam, se oni diras ion similas al "konstrui figuron en 4-spaco" ĉi tio subkomprenas iun tempon por konstrui, kaj entute iel aperas jam 5 koordinatoj - la 4 spacaj kaj tempo.

La 4-a spaca dimensio estas perpendikulara al la aliaj tri spacaj dimensioj. La vortoj por direktoj en la tri sciataj dimensioj povas esti ekzemple supren/suben (alto), nordo/sudo (latitudo), kaj oriento/okcidento (longitudo). Kiam oni parolas pri la kvara spaca dimensio, aldona paro de terminoj estas bezonata, sed dume ne estas sufiĉe agnoskita ĉi tiu paro de vortoj.

Se tempo estas grafita kiel la kvara dimensio, la aldona kvara spaca dimensio devas esti nomata kiel la kvina dimensio.

La kvara spaca dimensio kaj perpendikulareco

Kartezia geometrio elektas perpendikularajn direktojn tra spaco kiel dimensioj. La kvara dimensio estas pro tio la direkto en spaco kiu estas perpendikulara al ĉi tiuj tri la aliaj direktoj.

Objektoj kun ekde 1 ĝis 5 dimensioj

‎

La kutima eŭklida ebeno estas du-dimensia. Oni povas opinii ke la ebeno konsistas el familio de rektoj, paralelaj unu al la aliaj. Tiu rekto kiu enhavas la fonton estas la nula rekto. Por atingi iun punkton de la ebeno el la fonto, oni povas imagi vojaĝon komence laŭ la nula rekto al punkto la plej proksima al la dezirata, kaj tiam vojaĝon perpendikulare al la rektoj ĝis la dezirata punkto. Tiel la spaco estas du-dimensia - ĉiu el du partoj de la vojaĝo estas priskribata per skalara valoro, egala al la trairita distanco, kun signumo minuso asignita al unu direkto kaj signumo pluso asignita al la alia direkto, kaj ĉiu parto de la vojaĝo donas unu dimension.

La kutima eŭklida 3-spaco estas tri-dimensia. Oni povas opinii ke la spaco konsistas el stako de ebenoj, paralelaj unu al la aliaj. Tiu ebeno kiu enhavas la fonton estas la nula ebeno. Por atingi iun punkton de la spaco el la fonto, oni povas imagi vojaĝon komence laŭ la nula ebeno al punkto la plej proksima al la dezirata, kaj tiam vojaĝon perpendikulare al la ebenoj ĝis la dezirata punkto. Tiel la spaco estas tri-dimensia - du dimensioj estas donitaj de la unua parto de la vojaĝo, kaj unu dimensio estas donita de la dua.

La kvara spaca dimensio, do, povas esti priskribita kiel ekzisto de malfinia kvanto de paralelaj 3-dimensiaj spacoj. Por atingi iun punkton de la kvar-dimensia spaco, oni vojaĝas laŭ la tri-dimensia spaco, kaj poste ankaŭ tra la 3-spacoj laŭ la kvara dimensio. La tuteca kvanto de dimensioj estas kvar.

Difino

Matematike, la 4-dimensia eŭklida spaco (eŭklida 4-spaco) estas 4-dimensia normigita vektora spaco kun la eŭklida normo. La longo de vektoro

esprimita en la norma bazo estas

kio estas la ĝeneraligo de la pitagora teoremo al 4 dimensioj. Ĉi tio permesas difini la angulon inter du vektoroj (vidu en eŭklida spaco por plia informo).

Geometrio kun kvar spacaj dimensioj

Klaku por vidi animacion de 3D projekcio de turnanta 24-ĉelo. Ĝi turniĝas samtempe ĉirkaŭ du perpendikularaj ebenoj

En kvar spacaj dimensioj, eŭklida geometrio provizas pli grandan aron de diversaj geometriaj figuroj ol ekzisti en tri dimensioj. Simile al tio kiel tri-dimensiaj pluredroj estas spacaj ĉirkaŭbarataj per koneksaj du-dimensiaj edroj, la kvar-dimensiaj plurĉeloj estas ĉirkaŭbarataj per koneksaj tri-dimensia ĉeloj. En tri dimensioj estas akurate 5 regulaj konveksaj pluredroj, aŭ platonaj solidoj, sed 6 konveksaj regulaj plurĉeloj ekzistas en kvar dimensioj. Kvin el la ses povas esti interpretataj kiel naturaj vastigaĵoj de la platonaj solidoj, simele al tio kiel la kubo, (platona solido), estas natura vastigaĵo de la du-dimensia kvadrato.

Kvinĉelo estas konstruita el 5 kvaredroj por ĉeloj kaj estas la kvar-dimensia analogo de la kvaredro. 4-hiperkubo estas farita el 8 kubaj ĉeloj kaj estas la kvar-dimensia analogo de la kubo. 16-ĉelo estas la ekvivalento de la okedro.

Pli malsimplaj 120-ĉelo kaj 600-ĉelo estas analogoj al la dekduedro kaj dudekedro, respektive. La 24-ĉelo estas la unika regula plurĉelo kiu ne havas bonan regulan tri-dimensian ekvivalenton.

Estas ankaŭ granda aro de duonregulaj plurĉeloj (konveksaj uniformaj plurĉeloj), kaj multaj la aliaj la plej diversaj plurĉeloj.

Simile al kiel la kutima sfero estas pli konkrete 2-sfero kaj estas du-dimensia surfaco farita el ĉiuj punktoj samdistanca de donita centra punkto en tri-dimensia spaco, la 3-sfero estas aro de ĉiuj punktoj samdistancaj de donita centra punkto en kvar-dimensia spaco. Ĉiu tri-dimensia sekco de 3-sfero per hiperebeno estas 2-sfero.

Dimensia analogeco

Por trairi el tri spacaj dimensioj al kvar, aparato nomata kiel dimensia analogeco estas kutime uzata. Dimensia analogeco estas studado de tio kiel n-1 dimensioj rilatas al n dimensioj, kaj tiam konkludado de tio kiel n dimensioj devus rilati al n+1 dimensioj.

Unu apliko de dimensia analogeco en bildigo de la kvara dimensio estas projekcioj. Projekcio estas maniero por prezenti n-dimensian objekton en n-1 dimensioj. Ekzemple, komputila ekrano estas 2-dimensia, kaj ĝi montras 3-dimensiajn objektojn prezentante ilin en du dimensioj per forprenanto de informo pri la tria dimensio. En ĉi tiu okazo, profundo estas forprenita kaj anstataŭigita per malrekta informo. La retino de la okulo estas du-dimensia tabelo de sentiloj sed ĝi permesas la cerbo al percepti la naturon de tri-dimensiaj objektoj uzante malrekta informo (ombroj, deklivaj linioj, lorna vizio kaj tiel plu). Oni uzas perspektivon por doni ŝajnantan tri-dimensian profundon al du-dimensiaj bildoj.

Simile, 3 dimensiaj objektoj povas esti matematike projekciita al la 3 dimensioj, kie ili povas tiam esti pli oportune rigarditaj. En ĉi tiu okazo, la retino de la kvar-dimensia okulo estus tri-dimensia tabelo de sentiloj. Hipoteza estaĵo kun ĉi tia okulo devus percepti la naturon de kvar-dimensiaj objektoj uzante malrektan informon enhavatan en la bildo ricevita per la retino. Perspektiva projekcio de 4 dimensioj produktas similajn efikas kiel en la 3-dimensia okazo. Ĉi tio aldonas ŝajnantan 4-dimensian profundon al ĉi tiuj 3-dimensiaj bildoj.

Reto de 4-hiperkubo

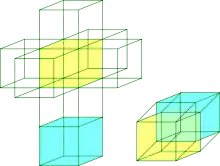
Dimensia analogeco helpas ankaŭ en komprenado de ĉi tiaj projekcioj. Ekzemple, 2-dimensiaj objektoj estas baritaj per unu-dimensiaj randoj: kvadrato estas barita per kvar lateroj. Tri-dimensia objektoj estas baritaj per du-dimensia surfacoj: kubo estas barita per 6 kvadratoj. Per aplikado de dimensia analogeco, oni povas konkludi ke 4-dimensia 4-hiperkubo estas barita per 3-dimensiaj volumenoj, kiuj estas 8 kuboj. Scio de ĉi tio estas ŝlosilo por kompreni kiel al interpreti tri-dimensian projekcion de la 4-hiperkubo. La randoj de la 4-hiperkubo projekciiĝas al volumenoj en la bildo, ne nur al 2-dimensiaj surfacoj.

Ankaŭ la koncepto de ombro povas helpi pli bone kompreni kvar dimensiojn. Se oni lumigas tri-dimensian objekton, ĝi devas disĵeti 2-dimensian ombron. Pro lumigo 2-dimensia objekto devas disĵeti 1-dimensian ombron (en du-dimensia mondo). Simile, lumigo der 4-dimensia objekto devus disĵeti 3-dimensian ombron.

Estante tri-dimensiaj oni povas nur vidi la mondon per okuloj en du dimensioj; kvar-dimensia estaĵo devas vidi la mondo en tri dimensioj. Tial ĉi tia estaĵo devas povi, ekzemple, vidi ĉiujn ses flankojn de netravidebla skatolo samtempe. Ĝi devus kapabli vidi ankaŭ tion kio estis en la skatolo samtempe. Ĝenerale, kvar-dimensia vidanto devas vidi ĉiujn punktojn de iu regiono en 3-dimensia spaco samtempe, inkluzivanta la enan strukturon de solidaj objektoj.

Rezonado analoge al familiaraj subaj dimensioj povas esti bonega intuicia gvido, sed oni devas zorgi ne akcepti rezultojn kiuj ne estas pli rigore testitaj. Ekzemple, konsideru la formulojn por la cirkonferenco de cirklo

C = 2π r ,

kaj la surfaca areo de sfero:

A = 4π r2 .

Malfacilas analoge al ili skribi korektan formulon por hipersurfaca volumeno de 3-sfero, kiu estas

V = 2π2 r3 ,

evidentas ke la radiuso r devas esti en la 3-a potenco, sed la koeficiento 2π2 estas ne tiel evidenta.

Vidu ankaŭ

Eksteraj ligiloj

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.