Zirkel
Der Zirkel (althochdeutsch circil, von lateinisch circulus „Kreisbahn“) ist ein Zeichengerät zum Zeichnen von Kreisen bzw. (allgemeiner) zum Übertragen von Distanzen. Außerdem ist er ein in der ebenen Euklidischen Geometrie verwendetes mathematisches Instrument, das einen Kreis um einen gegebenen Punkt zieht. Eine Sonderform von Zirkeln sind Ellipsenzirkel,[1] die das Zeichnen von Ellipsen erlauben.
Geschichte, Philosophie und Mathematik
In der Antike war der Zirkel neben dem Lineal das einzige Hilfsmittel zur Konstruktion geometrischer Objekte.
Auch im Mathematik-Unterricht (Geometrie, Konstruktion) sind Zirkel und Lineal die einzigen Hilfsmittel, um geometrische Zeichenoperationen (Parallelverschiebung von Geraden, Errichten der Senkrechten auf einer Gerade, der Mittelsenkrechten auf einer Strecke, Konstruktion von Dreiecken, Trapezen, Parallelogrammen, Rechtecken, regelmäßigen Sechsecken usw.) auszuführen.
Heute wird im Schulunterricht neben dem Zirkel und Lineal auch das Geodreieck und Dynamische Geometrie-Software benutzt.
Die entsprechenden Operationen werden auch beim CAD benötigt und teilweise automatisch ausgeführt.
Beschreibung des Zirkels
Das Zeichengerät Zirkel besteht aus zwei gleich langen, üblicherweise metallenen Stäben, die jeweils an einem Ende gelenkig verbunden sind. Einer der Stäbe hat an seinem anderen Ende eine Spitze (Nadel), die zur Fixierung des Zirkels auf der Unterlage dient. Mit dem Fixieren wird der Kreismittelpunkt festgelegt, mit dem Abstand des zweiten Schenkels zum ersten der Radius.
Am Ende des zweiten, beweglichen Stabes befindet sich in der Regel eine Vorrichtung, mit der der Kreis oder Kreisabschnitt auf der Unterlage gezeichnet wird. Zum Zeichnen werden abhängig vom Untergrund verschiedene Vorrichtungen angewendet. Auf Papier wird eine Bleistiftmine (in der Schule) oder eine Vorrichtung für Tusche (technische Zeichnungen) auf Pergament verwendet. Für Darstellungen von Kreisen auf anderen Materialien, beispielsweise Leder, wird Kreide verwendet. Auf metallenen Oberflächen kommt eine Reißnadel zum Einsatz. Kreide-Zirkel für Schultafeln (besonders aus Mattglas) haben meist einen Mittelpunktsschenkel, der mit einem Kugelgelenk an der Spitze eines flachen Dreibeins sitzt. Die Beine tragen Gummifüße oder Saugnäpfe, ein mittiger weißer Visierkegel weist zum Mittelpunkt auf der Tafel.
Der Winkelabstand der Schenkel bestimmt den Kreisradius und wird am einfachsten durch (meist justierbare) Reibung der Schenkelanlenkung(en) festgehalten. Zahnradgetriebe oder Symmetrierhebel stellen den gerändelten Drehzapfen am Zirkelkopf senkrecht. Schnellverstellzirkel tragen am Kopf eine starke Feder, die das Walzenlager presst, den Griff symmetrisch hält und die Schenkel sanft zusammendrückt. Eine Stange mit gegenläufigen Gewinden und einhändig bedienbarem Mitteltrieb-Rändelrad spreizt die Schenkel justierbar. Sich auf Fingerdruck öffnende und dann verschiebbare Muttern oder Gewinde mit sehr großen Steigungen (diese in eng gleitenden Kunststoffmuttern) ermöglichen noch schnellere Radiusverstellung. Schneiderzirkel aus Holz und einfache Zirkel für Metallbau oder Zimmerer weisen häufig einen (eventuell geschlitzten) Blechbogen auf, der zusammen mit einer Klemmschraube den eingestellten Schenkelwinkel fixiert.
Spezielle Zirkel enthalten am eingestochenen, fest stehenden Schenkel eine Millimeterteilung oder einen Nonius. Der genaue Abstand zwischen den Schenkelspitzen wird am beweglichen Schenkel abgelesen.
Varianten
Aus dem Bereich der Ideenlehre („Konstruktion mit Zirkel und Lineal“) kommt die Unterscheidung zwischen kollabierendem und nichtkollabierendem Zirkel. Ein kollabierender Zirkel ist üblicherweise ein rein gedankliches Werkzeug – ein Zirkel, mit dem man keinen Radius abnehmen und zu einem anderen Mittelpunkt übertragen kann, da er beim Abheben zuschnappen würde –, während real existierende Zirkel praktisch immer nichtkollabierende Zirkel sind; siehe dazu den Hauptartikel kollabierender Zirkel. Die folgenden Varianten sind alle nicht-kollabierend.
Stechzirkel
Stechzirkel oder Einhandzirkel haben zwei Spitzen, je eine je Schenkel. Sie zeichnen nicht, sondern dienen zum Abgreifen von Längen. Durch mehrfaches Einstechen und Weiterzirkeln können auch Längen bestimmt werden. Das funktioniert näherungsweise auch entlang von Kurven oder zum Erzeugen von Einstichen in gleichmäßigen Abständen entlang von Kurven oder Linien.
In der Seefahrt zur Navigation dienen Stechzirkel zum Abgreifen von Strecken und Entfernungen auf Seekarten.
Navigationszirkel
In der geometrischen Konstruktion von Gliederketten oder Wellenerscheinungen. Stechzirkel werden von Steinmetzen auch zum Einritzen von radialen Linien in einen Naturstein verwendet, der von ihnen bearbeitet wird.
Ein sogenannter Feldzirkel ist ein größerer, von einer stehenden Person zu bedienender Stechzirkel, der zum Abmessen von Entfernungen in der freien Natur, auf landwirtschaftlichen Feldern oder auch in der Archäologie verwendet wird. Er ist auf ein festes Maß einstellbar (meist 1 Meter). Er erreicht nicht die Genauigkeit eines Messbandes, ist aber genauer als Schätzen und reicht für viele Zwecke aus.
Fallnullenzirkel
Zum Zeichnen sehr kleiner Kreise hinunter bis zu einem Durchmesser von etwa einem Millimeter dienen Fallnullenzirkel. Die Achse wird mit ihrer Spitze angesetzt, der Schenkel wird fallengelassen und zum Zeichnen rotiert.
Stangenzirkel
Zum Zeichnen großer Kreise (bis 60 cm Radius) verwendet man einen sogenannten Stangenzirkel, bei dem die beiden Punkte (Kreismittelpunkt und Radius) an einer Metallstange parallel verschoben werden können.
Schultafel-Zirkel
Zum Zeichnen von Kreisen und Kreisformen auf Schulwandtafeln werden große Zirkel verwendet, die an einem Schenkel eine Tafelkreide aufnehmen können und am anderen Schenkel statt einer Spitze einen kleinen Gummisauger haben. Die Schenkel sind etwa 50 cm lang.
Improvisierte Zirkel
Ein einfacher Zirkel lässt sich aus einem Nagel oder einer Nadel zum Festlegen des Mittelpunkts, einem Faden oder einer Schnur zur Bestimmung des Radius und einem Stift zum Zeichnen konstruieren. Die Enden des Fadens werden um Stift und Nagel gewickelt, der passende Radius muss durch Probieren mittels Aufwickeln ermittelt werden (Siehe hierzu auch Gärtnerkonstruktion). Auch eine Schnurschlinge oder dünner Karton, durchstochen an zwei Stellen, kommen in Betracht.
Weitere Varianten: Greifzirkel, Hohlzirkel
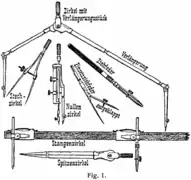Historische Ausführungen
Schneidezirkel und Schulzirkel
Fallnullenzirkel
Stangenzirkel
Ein Zirkelkasten des Herstellers Johann Christian Lotter
Symbolik des Zirkels
Im Mittelalter wurde der Zirkel zum Symbol der Geometrie, der kosmischen Ordnung und Planungsarbeit, insbesondere in der Baukunst sowie Erd-, Land- und Stadtvermessung. In der bildenden Kunst zeigen Buchmalereien den Weltenrichter als Geometer, der den Erdkreis vermisst. Der Zirkel ist mit dem Winkelmaß und dem heiligen Buch noch heute ein Symbol der Freimaurerei, das den Baubruderschaften der Dombauhütten entlehnt wurde, die diese Kombination als Symbol führten. Ein Zirkel ist eines der Attribute der Temperantia, der Personifikation der Mäßigung und Besonnenheit, und der personifizierten Melancholie wie z. B. in Albrecht Dürers Kupferstich Melencolia I (1514).
Im 20. Jahrhundert gehört der Zirkel zusammen mit dem Hammer und Ährenkranz in Form eines Lorbeerkranzes zum Emblem des Arbeiter- und Bauernstaates DDR. Er versinnbildlichte darin die Intellektuellen (im Sprachgebrauch der DDR als „Schicht der Intelligenz“ bezeichnet), während Hammer und Ähren für die Arbeiter bzw. Bauernschaft standen. Eine davon losgelöste Symbolik umfasst das Wappen von Langenstein (Oberösterreich). Der Zirkel steht zudem in der Kunstrichtung Sozialistischer Realismus.
_British_Museum.jpg.webp)
The Ancient of Days (1794) von William Blake
Zirkel im Staatsemblem der DDR
-Stemma.png.webp)
Siehe auch
Weblinks
- Historie: Spezialisierung und Generalisierung in der Entwicklung der Zirkel. (PDF; 0,7 MB) history.didaktik.mathematik.uni-wuerzburg.de
Einzelnachweise
- Ellipsenzirkel. In: Meyers Großes Konversations-Lexikon. 6. Auflage. Band 5: Differenzgeschäfte–Erde. Bibliographisches Institut, Leipzig / Wien 1906, S. 720–721 (Digitalisat. zeno.org).