Würfel von Tuscania
Die Würfel von Tuscania (früher Würfel von Toscanella) sind zwei etruskische Artefakte aus dem 5. bis 1. Jahrhundert v. Chr. und dienten als Spielwürfel. Die Würfel wurden nach ihrem wahrscheinlichen Herkunftsort Tuscania benannt und befinden sich heute in der Bibliothèque nationale de France in Paris. Auf den Würfeln sind die Anzahl der Augen als Zahlwörter in etruskischer Schrift eingraviert. Insofern sind die Würfel von großer Bedeutung für die Entschlüsselung etruskischer Zahlwörter und die Einordnung der etruskischen Sprache.

Entdeckung

Die Würfel wurden im Februar 1848 von Domenico Campanari entdeckt und stammen aus Tuscania oder dem benachbarten Vulci. Beide Orte liegen in der italienischen Region Latium und waren bedeutende etruskische Siedlungen. Tuscania hieß vom Mittelalter bis 1911 Toscanella. Die Würfel gelangten anschließend in den Besitz von Honoré Théodoric d’Albert de Luynes (1802–1867), der sie 1862 dem französischen Staat als Schenkung vermachte. Seitdem werden die Spielwürfel unter den Archivbezeichnungen Luynes.816 und Luynes.817 in der Nationalbibliothek von Frankreich aufbewahrt. Erstmals erwähnt und beschrieben wurden die Würfel 1848 im Bullettino dell'Instituto di corrispondenza archeologica.
Beschreibung
Die Würfel sind aus Elfenbein gefertigt und besitzen eine Kantenlänge von etwa 2,4 cm, wobei die Kanten unterschiedlich lang sind und ihre Maße von 2,3 bis 2,5 cm variieren. Die Spielwürfel entsprechen daher nur annähernd einem geometrischen Würfel. Die Seitenflächen sind keine Quadrate und allenfalls gegenüberliegende Seiten haben nahezu gleiche Form und Größe. Hinsichtlich ihrer Anordnung auf den Seitenflächen und der Schreibung sind die Gravuren auf beiden Würfeln identisch. Es sind die einzigen etruskischen Spielwürfel, auf denen keine Augen, sondern Schriftzeichen eingraviert sind.
Inschriften

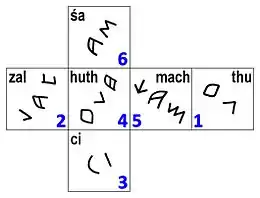
Die Inschriften sind in etruskischer Schrift verfasst. Die Buchstaben sind entsprechend den etruskischen Schreibgewohnheiten von rechts nach links angeordnet. Da die Etrusker die Buchstaben aus einem westgriechischen Alphabet übernommen haben, stellt die Entzifferung kein Problem dar. Die Inschriften gegenüberliegender Seiten bilden insgesamt drei Paare, die transkribiert lauten:
thu – huth | zal – mach | ci – śa.
Buchstaben in der eingravierten Form waren vom 5. bis zum 1. Jahrhundert v. Chr. in Gebrauch. Allerdings kann die Bedeutung der Zahlwörter nicht unmittelbar angegeben werden, da es an einer Bilingue mangelt, in der ein Text mit Zahlwörtern auf Etruskisch und in einer anderen Sprache verfasst ist, und auch kein etruskischer Text vorliegt, in dem Zahlen gleichzeitig in Zahlschrift mit Ziffern und in Zahlwörtern mit Buchstaben vorkommen.
Deutung
Die nachfolgende Übersicht zeigt die Zuordnungen der Zahlwörter zu den Zahlen von 1 bis 6 von verschiedenen Autoren.
| Autor | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Bullettino (1848) | mach | thu | zal | huth | ci | śa |
| Alf Torp (1905) | thu | zal | ci | śa | mach | huth |
| Emil Goldmann (1929) | mach | thu | ci | śa | huth | zal |
| Hans Lorenz Stoltenberg (1943) | thu | zal | ci | huth | mach | śa |
| Karl Olzscha (1957) | thu | zal | ci | huth | mach | śa |
| Ambros Pfiffig (1969) | thu | zal | ci | śa | mach | huth |
| Mauro Cristofani (1973) | thu | zal | ci | huth ? | mach | śa ? |
| Angelo Savelli (1976) | thu | huth | zal | mach | ci | śa |
| Massimo Pallottino (1984) | thu | zal | ci | huth ? | mach | śa ? |
| Helmut Rix (1985) | thu | zal | ci | huth | mach | śa |
| Alessandro Morandi (1991) | thu | zal | ci | huth | mach | śa |
| Luciano Agostiniani (1995) | thu | zal | ci | śa | mach | huth |
| Massimo Pittau (1997) | thu | zal | ci | huth | mach | śa |
| Bonfante und Bonfante (2002) | thu | zal | ci | śa | mach | huth |
| Fred C. Woudhuizen (2019) | zal | thu | ci | huth | mach | śa |
Unstrittig scheint inzwischen die Identifizierung von thu mit 1, zal mit 2, ci mit 3 und mach mit 5. Dementsprechend liegt auf beiden Würfeln 1 gegenüber huth, 2 gegenüber 5, und 3 gegenüber śa. Die beiden häufigsten Anordnungen gegenüberliegender Augenzahlen bei etruskischen Würfeln sind (1–6, 2–5, 3–4) und (1–2, 3–4, 5–6) und folgen der Additionsregel „Die Augensumme ist 7“ bzw. der Subtraktionsregel „Die Augendifferenz ist 1“. Die Subtraktionsregel könnte nur dann gelten, wenn huth weder 4 noch 6, sondern 2 ist, wie Savelli (1976) vermutet. Sofern die Inschriften der Summenregel folgen, ist huth mit 6 und śa mit 4 zu identifizieren.

Allerdings könnte die Anordnung der Augenzahlen auch einer anderen Regel folgen. Nach Olzscha (1957) würde die Identifizierung von huth mit 4 und śa mit 6 mit (1–4, 2–5, 3–6) eine Subtraktionsregel der Form „Die Augendifferenz ist 3“ erfüllen. Dafür spricht, dass noch andere etruskische Würfeltypen gefunden wurden. Allerdings hat man im südlichen Etrurien, wo die beiden Würfel herstammen, nur Spielwürfel mit den Anordnungen (1–6, 2–5, 3–4) oder (1–2, 3–4, 5–6) entdeckt. Bis etwa 500 v. Chr. wurden in dieser Region Würfel ausschließlich nach der Subtraktionsregel „Die Augendifferenz ist 1“ angefertigt, dann kamen beide Regeln zur Anwendung und ab 350 v. Chr. finden sich nur noch Würfel nach der Additionsregel. Ein etruskischer Würfel mit der Anordnung (1–4, 2–5, 3–6) ist bis heute noch nicht entdeckt worden. Zahlreiche Etruskologen halten aber an der Identifizierung von huth mit 4 und śa mit 6 fest und begründen dies etymologisch unter der Annahme, dass das Etruskische zu den indogermanischen Sprachen zählt oder zumindest von diesen stark beeinflusst wurde.
Literatur
- Bullettino dell'Instituto di corrispondenza archeologica. Rom 1848, S. 60 und 74 (online).
- Alf Torp: Etruscan notes. Nabu Press, Charleston 2011, Nachdruck des Originals von 1905, ISBN 9781246416893.
- Emil Goldmann: Beiträge zur Lehre vom indogermanischen Charakter der etruskischen Sprache. Salzwasser-Verlag, Nachdruck des Originals von 1929, 2016, ISBN 9783846072851, S. 86–120.
- Hans Lorenz Stoltenberg: Die Bedeutung der etruskischen Zahlnamen. In: Glotta. Zeitschrift für griechische und lateinische Sprache. Band 30, 1943, S. 234–244.
- Karl Olzscha: Schrift und Sprache der Etrusker. In: Historia. Zeitschrift für Alte Geschichte. Band 6, Heft 1, 1957, S. 34–52.
- Ambros Josef Pfiffig: Die etruskische Sprache. Versuch einer Gesamtdarstellung. Akademische Druck- und Verlags-Anstalt, Graz 1969, S. 123 f.
- Mauro Cristofani: Introduzione allo studio dell'etrusco. Olschki, Florenz 1973.
- Angelo Savelli: I dadi del Museo civico e il problema dei numerali estruschi. In: Strenna storica bolognese. Band 26, 1976, S. 271–290.
- Massimo Pallottino: Etruskologie: Geschichte und Kultur der Etrusker. Neuauflage. Springer, Basel 1984, S. 461 f.
- Helmut Rix: Schrift und Sprache. In: Mauro Cristofani (Hrsg.): Die Etrusker. Belser Verlag, Stuttgart 1985, S. 210–238.
- Alessandro Morandi: Nuovi Lineamenti di Lingua Etrusca. Erre Emme, Rom 1991, S. 81–86.
- Luciano Agostiniani: Sui numerali etruschi e la loro rappresentazione grafica. In: AION Linguistica. Band 17, 1995, S. 21–65.
- Massimo Pittau: La Lingua Etrusca: Grammatica e Lessico. Insula Edizioni, Nuoro 1997, ISBN 888611107X, S. 72–76.
- Giuliano Bonfante, Larissa Bonfante: The Etruscan Language: An Introduction. 2. Auflage. Manchester University Press, Manchester/New York 2002, ISBN 0719055407, S. 96–97.
- Gilberto Artioli, Vincenzo Nociti, Ivana Angelini: Gambling with etruscan dice: A tale of numbers and letters. In: Archaeometry. Band 53, Heft 5, Oxford 2011, S. 1031–1043 (online).
- Fred C. Woudhuizen: Etruscan as a Colonial Luwian Language: The Comprehensive Version (= Maarten D. de Weerd, Jan P. Stronk [Hrsg.]: Publications of the Henry Frankfort Foundation. Band 16). Dutch Archaeological and Historical Society, 2019, ISSN 1574-1370, Structurally transparent texts: Etruscan numerals in Indo-European perspective, S. 192 (englisch, academia.edu).
Weblinks
- Bibliothèque nationale de France: Luynes.816 Luynes.817 (französisch)
- Massimo Pittau: I numerali etruschi (italienisch)