Vierzehneck
Ein Vierzehneck oder Tetradekagon ist ein Polygon mit 14 Seiten und 14 Ecken. Oft ist dabei ein ebenes, regelmäßiges Vierzehneck gemeint, bei dem alle Seiten gleich lang sind und alle Eckpunkte auf einem gemeinsamen Umkreis liegen.
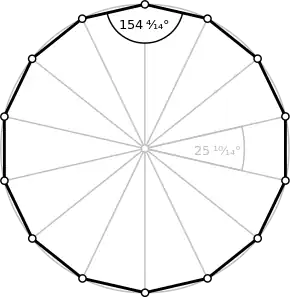
Regelmäßiges Vierzehneck
Das regelmäßige Vierzehneck ist nach Carl Friedrich Gauß und Pierre-Laurent Wantzel kein konstruierbares Polygon, denn seine Seitenanzahl ist kein Produkt einer Zweierpotenz mit paarweise voneinander verschiedenen Fermatschen Primzahlen.
Größen
| Größen eines regelmäßigen Vierzehnecks | ||
|---|---|---|
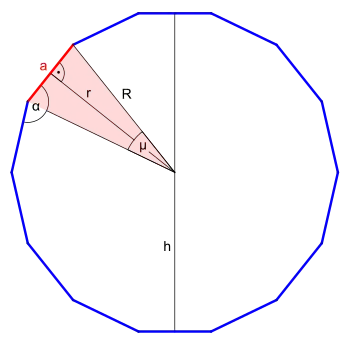
| Innenwinkel |
| |
| Zentriwinkel
(Mittelpunktswinkel) |
||
| Seitenlänge | ||
| Umkreisradius | ||
| Inkreisradius | ||
| Höhe | ||
| Flächeninhalt | mit Seitenlänge
mit Umkreisradius | |
Mathematische Zusammenhänge
Innenwinkel
Der Innenwinkel wird von zwei benachbarten Seitenlängen eingeschlossen.
- .
Zentriwinkel
Der Zentriwinkel oder Mittelpunktswinkel wird von zwei benachbarten Umkreisradien eingeschlossen.
- .
Seitenlänge
Die Seitenlänge errechnet sich
- .
Umkreisradius
Der Radius des Umkreises ergibt sich durch Umformen der Formel für die Seitenlänge .
- .
Inkreisradius
Der Inkreisradius ist die Höhe eines gleichschenkligen Teildreiecks mit den beiden Schenkeln gleich dem Umkreisradius und der Grundlinie gleich der Seitenlänge .
- .
Höhe
Die Höhe eines regelmäßigen Vierzehneckes ergibt sich aus der Summe von zwei Inkreisradien
- .
Flächeninhalt
Mithilfe der Seitenlänge
Die Fläche eines regelmäßigen Vierzehnecks mit Seitenlänge wird durch die Formel gegeben
- .
Mithilfe des Umkreisradius
Der Flächeninhalt eines Dreiecks berechnet sich allgemein . Für die Berechnung des Vierzehnecks werden die Ergebnisse der Seitenlänge und des Inkreisradius herangezogen, worin für die Höhe eingesetzt wird.
- daraus folgt für die Fläche eines Teildreiecks
- zusammengefasst ergibt sich
und für die Fläche des gesamten Vierzehnecks
- .
Geometrische Konstruktionen
Ein regelmäßiges Vierzehneck kann nicht allein als Konstruktion mit Zirkel und Lineal dargestellt werden; es ist kein konstruierbares Polygon. Nimmt man jedoch zu diesen klassischen (euklidischen) Werkzeugen noch ein zusätzliches Hilfsmittel, wie z. B. einen Tomahawk zur Dreiteilung des Winkels oder ein Lineal mit einer bestimmten Markierung, ist eine exakte Konstruktion möglich. Grundsätzlich kann aus der Konstruktion eines Siebenecks, z. B. durch zusätzliche Halbierung des Zentriwinkel, ein regelmäßiges Vierzehneck gewonnen werden.
Tomahawk als zusätzliches Hilfsmittel
Andrew M. Gleason veröffentlichte 1988 in der mathematische Zeitschrift The American Mathematical Monthly zwei elegante Konstruktionen zu den regulären Polygonen Siebeneck und Dreizehneck, die zur Lösung eine Dreiteilung des Winkels benötigen. Das Prinzip der Dreiteilung ist in keinem der beiden Konstruktionen festgelegt.[1]
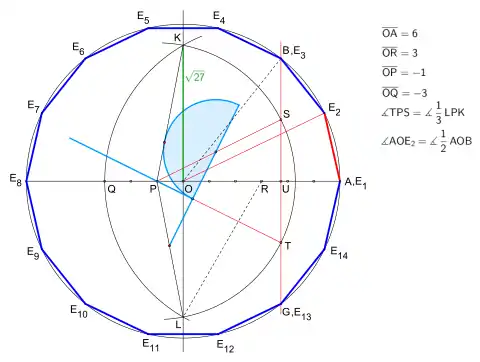
eine Abwandlung der Konstruktion des Siebenecks mit Tomahawk.

Bei gegebenem Umkreis (siehe Bild 1)
Der folgende Konstruktionsplan für das Vierzehneck, ist nahezu gleich dem Original des Siebenecks von Andrew M. Gleason:
Es beginnt im Koordinatenursprung eines kartesischen Koordinatensystems im Punkt mit einem Kreis mit Radius Es folgt die Festlegung der Punkte und . Anschließend werden die Punkte und bestimmt, sie sind Eckpunkte zweier gleichseitiger Dreiecke mit Basis . Nach dem Verbinden der Punkte und mit in der Original-Zeichnung aus der Zeitschrift The American Mathematical Monthly, siehe Einzelnachweise, ist dieser Punkt zwischen und , wird um ein Kreisbogen von bis gezogen. Nun drittelt man den Winkel mit einer freiwählbaren Methode (z. B. Kurven, Tomahawk etc.), dabei ergeben sich die Punkte und . Eine Gerade durch und ergibt und , die zusammen mit Eckpunkte eines regelmäßigen Siebenecks sind.
Nun bedarf es noch einer Halbierung des Zentriwinkels des Siebenecks und man erhält so den zweiten Eckpunkt des gesuchten Vierzehnecks. Die übrigen Eckpunkte können durch Verwendung des Kreisbogens nacheinander gefunden werden.
Markiertes Lineal als zusätzliches Hilfsmittel

David Johnson Leisk, meist bekannt als Crockett Johnson, veröffentlichte 1975 eine sogenannte Neusis-Konstruktion eines Siebenecks (Heptagon), bei dem die Seitenlänge gegeben ist.[2] Hierfür verwendete er einen Zirkel und ein spezielles Lineal, auf dem eine Markierung angebracht war.
Bei gegebener Seitenlänge (siehe Bild 2)
- Errichte senkrecht zur Seitenlänge im Punkt die Strecke , sie ist gleich lang wie die Seitenlänge
- Verbinde den Punkt mit z. B. bei einer Seitenlänge hat die Diagonale den Wert
- Halbiere die Seitenlänge , es ergibt sich der Punkt
- Errichte eine Senkrechte auf die Seitenlänge im Punkt
- Ziehe den Kreisbogen mit dem Radius um den Punkt und durch den Punkt
- Setze das mit dem Punkt markierte Lineal (Abstand Ecke Lineal bis Punkt entspricht ) auf die Zeichnung. Drehe und schiebe das Lineal bis dessen Ecke auf der Mittelsenkrechten anliegt, die Markierung Punkt auf dem Kreisbogen aufliegt und die Kante des Lineals durch den Punkt verläuft, es ergibt sich der Punkt
- Verbinde den Punkt mit dem Punkt , der dadurch entstandene Winkel , mit (Theta) bezeichnet, entspricht einem Viertel des Zentriwinkels eines Siebenecks, aufgrund des 2. Strahlensatzes entspricht er auch einer Hälfte des gesuchten Zentriwinkels des Vierzehnecks.
- Ziehe um den Punkt einen Kreis durch es ist der Umkreis des entstehenden Vierzehnecks.
- Bestimme mit der Seitenlänge die restlichen zwölf Eckpunkte des Siebenecks und verbinde abschließend die benachbarten Eckpunkte miteinander. Somit entsteht das regelmäßige Vierzehneck
Näherungskonstruktion

Bild 3 zeigt ein Vierzehneck in seinem Umkreis, erstellt mit einer universellen Methode.[3][4]
Zuerst wird die Strecke , später der Durchmesser des gesuchten Vierzehnecks, in gleich lange Teile mithilfe des Strahlensatzes geteilt (in der Zeichnung nicht dargestellt) oder mittels Aneinanderreihen von gleich langen Abständen bestimmt. Es werden entweder die geraden oder die ungeraden Zahlen (Teilungspunkte) auf markiert. In diesem Beispiel sind die ungeraden Zahlen und eingetragen, dadurch liegen z. B. die späteren Eckpunkte und nicht in der Nähe des Punktes . Der Teilungspunkt entspricht dem Mittelpunkt des Durchmesser Nun wird um den Mittelpunkt und durch der Umkreis gezogen. Die zwei darauffolgenden Kreisbögen um bzw. mit dem Radius schneiden sich in den Punkten und Nach deren Verbindung erhält man die Mittelachse und als Schnittpunkte die Eckpunkte und des entstehenden Vierzehnecks.
Es geht weiter mit dem Festlegen der Eckpunkte auf dem Umkreis. Das Lineal wird an den Punkt und an die ungerade Zahl gelegt. Danach am Lineal entlang eine Linie bis zur gegenüberliegenden Hälfte der Umkreislinie gezogen, ergibt den Eckpunkt Diese Vorgehensweise wiederholt sich beim Bestimmen des Eckpunktes sowie ausgehend vom Punkt beim Festlegen der Eckpunkte und Es folgt das Verbinden des Eckpunktes mit . Somit ist die Strecke die erste annähernd konstruierte Seitenlänge des gesuchten Vierzehnecks.
Zunächst sind auf der unteren Hälfte des Umkreises die noch fehlenden Eckpunkte in der Reihenfolge und durch mehrmaliges Abtragen der Seitenlänge festzulegen sowie danach die noch fehlenden Eckpunkte in der Reihenfolge und auf der oberen Hälfte des Umkreises. Abschließend werden die benachbarten Eckpunkte miteinander verbunden.
Zwei der Seiten dieses Vierzehnecks haben zwar die gleiche Länge, aber eine von den anderen unterschiedliche; es sind dies die Seiten und Die übrigen zwölf Seitenlängen sind gleich lang.
Größter und kleinster absoluter Fehler der Seitenlängen bei einem Umkreisradius mit :
- und
Die übrigen zwölf Seitenlängen
Regelmäßige überschlagene Vierzehnecke
Ein regelmäßiges überschlagenes Vierzehneck ergibt sich, wenn beim Verbinden der vierzehn Eckpunkte jedes Mal mindestens einer übersprungen wird und die somit erzeugten Sehnen gleich lang sind. Notiert werden solche regelmäßigen Sterne mit Schläfli-Symbolen , wobei die Anzahl der Eckpunkte angibt und jeder -te Punkt verbunden wird.
Es gibt nur zwei regelmäßige Vierzehnstrahlsterne.
Die Sterne mit den Symbolen {14/2} und {14/12} sind regelmäßige Siebenecke, {14/4} und {14/10} sowie {14/6} und {14/8} sind regelmäßige Heptagramme.
- Regelmäßige Vierzehnstrahlsterne


Literatur
- H. Maser: Die Teilung des Kreises …, Artikel 365., in Carl Friedrich Gauss' Untersuchungen über höhere Arithmetik, Verlag von Julius Springer, Berlin 1889; Göttinger Digitalisierungszentrum, Universität Göttingen; abgerufen am 15. März 2018.
Weblinks
Einzelnachweise
- Andrew Gleason: Angle Trisection, the Heptagon, and the Triskaidecagon. In: The American Mathematical Monthly. Band 95, Nr. 3, 1988, S. 185–194, 186 ff., JSTOR:2323624 (math.fau.edu, FIG.1. Construction of a regular heptagon [PDF; 303 kB; abgerufen am 21. Mai 2019]).
- Weisstein, Eric W. „Heptagon.“ From MathWorld, A Wolfram Web Resource.
- H. August: Zeichnerische Konstruktion eines Elfecks. In: Zeichnerische Konstruktionen: Mehrecke. Abgerufen am 3. Januar 2018.
- Peter Eckardt: Siebeneck. In: Sterne und Polygone. Abgerufen am 3. Januar 2018.