Untermatrix
Eine Untermatrix, auch Teilmatrix oder Streichungsmatrix,[1] ist in der Mathematik eine Matrix, die durch Streichen von Zeilen und Spalten aus einer gegebenen Matrix entsteht. Eine Untermatrix einer quadratischen Matrix, bei der die gleichen Zeilen und Spalten gestrichen werden, wird auch als Hauptuntermatrix bezeichnet. Untermatrizen werden unter anderem zur Definition der Minoren und der Kofaktoren einer Matrix verwendet. Sie spielen eine wichtige Rolle im laplaceschen Entwicklungssatz der Determinante einer Matrix.
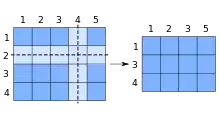
Definition
Ist eine Matrix über dem Körper , dann ist eine Untermatrix von eine Matrix, die dadurch entsteht, dass die Zeilen der Indexmenge und die Spalten der Indexmenge aus gestrichen werden, das heißt:
Die Untermatrix besitzt dann Zeilen und Spalten. Im Fall einelementiger Indexmengen schreibt man auch kurz statt . Falls und sind, wird eine Untermatrix
- bzw.
auch als Hauptuntermatrix bezeichnet. Gelegentlich wird eine Untermatrix auch dadurch notiert, dass die Zeilen und Spalten, aus denen sie besteht, als Indizes angegeben werden. Man schreibt dann:[2]
Im Folgenden wird jedoch erstere Notationsvariante verwendet. Untermatrizen, die aus aufeinanderfolgenden Zeilen- und Spaltenindizes aufgebaut sind, bilden einen Block einer Matrix.
Beispiel
Gegeben sei die reelle Matrix
- ,
dann ist die Untermatrix
diejenige Matrix, die durch Streichung der zweiten Zeile und der dritten Spalte entsteht.
Verwendung
Jede Matrix mit Rang besitzt eine quadratische Untermatrix , sodass
gilt und ihre Determinante
ist.[3] Eine solche Untermatrix kann beispielsweise mit Hilfe des gaußschen Eliminationsverfahrens gefunden werden. Die Determinante einer quadratischen Untermatrix wird auch als Minor oder Unterdeterminante bezeichnet. Die Determinante einer Hauptuntermatrix heißt entsprechend Hauptminor. Die Determinanten der Untermatrizen einer quadratischen Matrix werden mit alternierenden Vorzeichen versehen Kofaktoren
der Matrix genannt. Mit Hilfe der Kofaktormatrix kann die Inverse der Matrix explizit angegeben werden. Untermatrizen spielen auch eine wichtige Rolle im laplaceschen Entwicklungssatz der Determinante einer Matrix und im Satz von Binet-Cauchy zur Bestimmung der Determinante des Produkts zweier Matrizen.
Literatur
- Siegfried Bosch: Lineare Algebra. Springer, 2006, ISBN 3-540-29884-3.
- Christoph W. Überhuber: Computer-Numerik 2. Springer, 1995, ISBN 3-642-57794-6.
Einzelnachweise
- Christian Karpfinger: Höhere Mathematik in Rezepten. Springer Verlag, Berlin 2014, ISBN 978-3-642-37865-2, S. 95.
- Christoph Überhuber: Computer-Numerik 2. S. 212.
- Bosch: Lineare Algebra. S. 146.
Weblinks
- T. S. Pigolkina: Submatrix. In: Michiel Hazewinkel (Hrsg.): Encyclopedia of Mathematics. Springer-Verlag und EMS Press, Berlin 2002, ISBN 1-55608-010-7 (englisch, encyclopediaofmath.org).
- Eric W. Weisstein: Submatrix. In: MathWorld (englisch).
- Mathprof: Submatrix notation. In: PlanetMath. (englisch)