Taylorreihe

Die Taylorreihe wird in der Analysis verwendet, um eine analytische Funktion in der Umgebung einer Stelle durch eine Potenzreihe darzustellen, die der Grenzwert der Taylor-Polynome ist. Diese Reihenentwicklung wird Taylor-Entwicklung genannt. Reihe und Entwicklung sind nach dem britischen Mathematiker Brook Taylor benannt.

Approximation von ln(x) durch Taylorpolynome der Grade 1, 2, 3 bzw. 10 um die Entwicklungsstelle 1. Die Polynome konvergieren nur im Intervall (0, 2]. Der Konvergenzradius ist also 1.

Animation zur Approximation ln(1+x) an der Stelle x=0

Definition

Sei $I\subset \mathbb {R}$ ein offenes Intervall, $f\colon I\rightarrow \mathbb {R}$ eine glatte Funktion und $a$ ein Element von $I$ . Dann heißt die unendliche Reihe

Tf(x;a):=\sum _{n=0}^{\infty }{\frac {f^{(n)}(a)}{n!}}(x-a)^{n}=f(a)+f'(a)(x-a)+{\frac {f''(a)}{2}}(x-a)^{2}+{\frac {f'''(a)}{6}}(x-a)^{3}+\dotsb

die Taylorreihe von $f$ mit Entwicklungsstelle $a$ . Hierbei bezeichnet $n!$ die Fakultät von $n$ und $f^{(n)}$ die $n$ -te Ableitung von $f$ , wobei man $f^{(0)}:=f$ setzt.

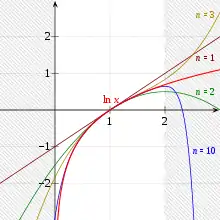
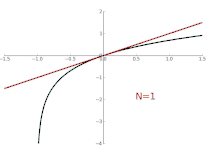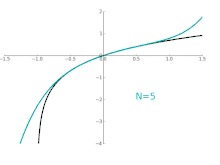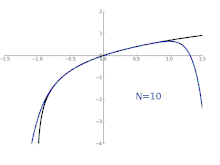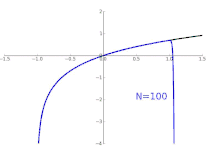
Die Reihe ist hier zunächst nur „formal“ zu verstehen. Das heißt, dass die Konvergenz der Reihe nicht vorausgesetzt ist. In der Tat gibt es Taylorreihen, die nicht überall konvergieren (für $T\log(x;1)$ siehe obige Abbildung). Auch gibt es Taylorreihen, die zwar konvergieren, aber nicht gegen die Funktion, aus der die Taylorreihe gebildet wird – zum Beispiel $Tf(x;0)$ für $f(x)={\begin{cases}\exp \left(-{\frac {1}{x^{2}}}\right)&{\text{für }}x\neq 0\\0&{\text{für }}x=0\end{cases}}.$

Im Spezialfall $a=0$ wird die Taylorreihe auch Maclaurin-Reihe genannt.

Die Summe der ersten beiden Terme der Taylorreihe

T_{1}f(x;a):=f(a)+f'(a)\cdot (x-a)

nennt man auch Linearisierung von $f$ an der Stelle $a$ . Allgemeiner nennt man die Partialsumme

T_{N}f(x;a):=\sum _{n=0}^{N}{\frac {f^{(n)}(a)}{n!}}(x-a)^{n},

die für festes $a$ ein Polynom in der Variablen $x$ darstellt, das $N$ -te Taylorpolynom.

Die Taylorformel mit Restglied macht Aussagen darüber, wie dieses Polynom von der Funktion $f$ abweicht. Aufgrund der Einfachheit der Polynomdarstellung sowie der guten Anwendbarkeit der Restgliedformeln sind Taylorpolynome ein häufig angewandtes Hilfsmittel der Analysis, der Numerik, der Physik und der Ingenieurwissenschaften.

Eigenschaften

Die Taylorreihe $Tf(x;a)$ zur Funktion $f$ ist eine Potenzreihe mit den Ableitungen

{\begin{aligned}\left(Tf\right)^{(k)}(x;a)&=\left({\frac {\mathrm {d} }{\mathrm {d} x}}\right)^{k-1}\sum _{n=0}^{\infty }{\frac {\mathrm {d} }{\mathrm {d} x}}\left({\frac {f^{(n)}(a)}{n!}}(x-a)^{n}\right)=\left({\frac {\mathrm {d} }{\mathrm {d} x}}\right)^{k-1}\sum _{n=1}^{\infty }{\frac {f^{(n)}(a)}{n!}}n(x-a)^{n-1}\\&=\left({\frac {\mathrm {d} }{\mathrm {d} x}}\right)^{k-1}\sum _{n=0}^{\infty }{\frac {f^{(n+1)}(a)}{n!}}(x-a)^{n}=\left(Tf'\right)^{(k-1)}(x;a)\end{aligned}}

und somit folgt durch vollständige Induktion:

\left(Tf\right)^{(k)}(x;a)=\left(Tf^{(k)}\right)(x;a)

Übereinstimmung an der Entwicklungsstelle

Wegen

\left(Tf\right)(a;a)=\sum _{n=0}^{\infty }{\frac {f^{(n)}(a)}{n!}}(a-a)^{n}={\frac {f^{(0)}(a)}{0!}}(a-a)^{0}=f(a)

stimmen an der Entwicklungsstelle $a$ die Taylorreihe $Tf$ und ihre Ableitungen mit der Funktion $f$ und deren Ableitungen überein:

\left(Tf\right)^{(k)}(a;a)=\left(Tf^{(k)}\right)(a;a)=f^{(k)}(a)

Gleichheit mit der Funktion

Im Fall einer analytischen Funktion $f(x)=\sum _{n=0}^{\infty }a_{n}(x-a)^{n}$ stimmt die Taylorreihe mit dieser Potenzreihe überein, denn es gilt

{\begin{aligned}f^{(k)}(x)&=\sum _{n=k}^{\infty }a_{n}{\frac {n!}{(n-k)!}}(x-a)^{n-k}\\{\frac {f^{(k)}(a)}{k!}}&=a_{k}\end{aligned}}

und somit $Tf(x;a)=f(x)$ .

Wichtige Taylorreihen

Exponentialfunktionen und Logarithmen

Animation zur Taylorreihenentwicklung der Exponentialfunktion an der Stelle x=0

Die natürliche Exponentialfunktion wird auf ganz $\mathbb {R}$ durch ihre Taylorreihe mit Entwicklungsstelle 0 dargestellt:

\mathrm {e} ^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}=1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+\dotsb \quad {\text{ für alle }}x\in \mathbb {R}

Beim natürlichen Logarithmus hat die Taylorreihe mit Entwicklungsstelle 1 den Konvergenzradius 1, d. h., für $0<x\leq 2$ wird die Logarithmusfunktion durch ihre Taylorreihe dargestellt (vgl. Abb. oben):

\ln(x)=\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}(x-1)^{n}=(x-1)-{\frac {(x-1)^{2}}{2}}+{\frac {(x-1)^{3}}{3}}-\dotsb \quad {\text{ für }}0<x\leq 2

Schneller konvergiert die Reihe

\ln \left({\frac {1+x}{1-x}}\right)=2\sum _{k=0}^{\infty }{\frac {x^{2k+1}}{2k+1}}=2x+{\frac {2}{3}}x^{3}+{\frac {2}{5}}x^{5}+\dotsb \qquad {\text{ für }}-1<x<1

und daher ist sie geeigneter für praktische Anwendungen.

Wählt man $x:={\frac {y-1}{y+1}}$ für ein $y>0$ , so ist $-1<x<1$ und $\ln \left({\frac {1+x}{1-x}}\right)=\ln(y)$ .

Trigonometrische Funktionen

Approximation von sin(x) durch Taylorpolynome T vom Grad 1, 3, 5 und 7

Animation: Die Kosinusfunktion um die Stelle 0 entwickelt, in sukzessiver Näherung

Für die Entwicklungsstelle $a=0$ (Maclaurin-Reihen) gilt:

{\begin{aligned}\sin(x)&=\sum _{n=0}^{\infty }(-1)^{n}{\frac {x^{2n+1}}{(2n+1)!}}&{\text{für alle}}\ x\\&=x-{\frac {x^{3}}{6}}+{\frac {x^{5}}{120}}-\dotsb \\\cos(x)&=\sum _{n=0}^{\infty }(-1)^{n}{\frac {x^{2n}}{(2n)!}}&{\text{für alle}}\ x\\&=1-{\frac {x^{2}}{2}}+{\frac {x^{4}}{24}}-\dotsb \\\tan(x)&=\sum _{n=1}^{\infty }{\frac {B_{2n}(-4)^{n}(1-4^{n})}{(2n)!}}x^{2n-1}&{\text{für }}|x|<{\frac {\pi }{2}}\\&=x+{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}+\dotsb \\\sec(x)&=\sum _{n=0}^{\infty }(-1)^{n}{\frac {E_{2n}}{(2n)!}}x^{2n}&{\text{für }}|x|<{\frac {\pi }{2}}\\&=1+{\frac {x^{2}}{2}}+{\frac {5x^{4}}{24}}+\dotsb \\\end{aligned}}

Hierbei ist $B_{2n}$ die $2n$ -te Bernoulli-Zahl und $E_{2n}$ die $2n$ -te Eulersche Zahl.

{\begin{aligned}\arcsin x&=\sum _{n=0}^{\infty }{\frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}\quad &{\text{für }}\left|x\right|<1\\\arccos x&={\frac {\pi }{2}}-\arcsin x&{\text{für }}\left|x\right|\leq 1\\\arctan x&=\sum _{n=0}^{\infty }(-1)^{n}{\frac {1}{2n+1}}x^{2n+1}&{\text{für }}\left|x\right|\leq 1\end{aligned}}

Produkt von Taylorreihen

Die Taylorreihe eines Produkts zweier reeller Funktionen $f$ und $g$ kann berechnet werden, wenn die Ableitungen dieser Funktionen an derselben Entwicklungsstelle $a$ bekannt sind:

f^{(n)}(a)=u_{n}\qquad g^{(n)}(a)=v_{n}

Mit Hilfe der Produktregel ergibt sich dann:

(f\cdot g)^{(n)}(a)=\sum _{k=0}^{n}{\binom {n}{k}}u_{k}v_{n-k}

Sind die Taylorreihen der beiden Funktionen explizit gegeben:

Tf(x;a)=\sum _{n=0}^{\infty }\alpha _{n}(x-a)^{n}\qquad Tg(x;a)=\sum _{n=0}^{\infty }\beta _{n}(x-a)^{n},

so gilt

T(f\cdot g)(x;a)=\sum _{n=0}^{\infty }\gamma _{n}(x-a)^{n}

mit

\gamma _{n}={\frac {(f\cdot g)^{(n)}(a)}{n!}}={\frac {1}{n!}}\sum _{k=0}^{n}{\frac {n!}{k!\,(n-k)!}}(k!\,\alpha _{k})((n-k)!\,\beta _{n-k})=\sum _{k=0}^{n}\alpha _{k}\beta _{n-k}.

Dies entspricht der Cauchy-Produktformel der beiden Potenzreihen.

Beispiel

Seien $f(x)=\exp(x)$ , $g(x)=1+x$ und $a=0$ . Dann gilt

\alpha _{n}={\frac {1}{n!}},\qquad \beta _{n}={\begin{cases}1&{\text{für }}n\in \{0,1\}\\0&{\text{für }}n>1\end{cases}}

und wir erhalten

\gamma _{0}=\alpha _{0}=1{\text{ für }}n=0,\qquad \gamma _{n}=\alpha _{n}+\alpha _{n-1}{\text{ für }}n>0,

in beiden Fällen also

\gamma _{n}={\frac {1+n}{n!}},

und somit

T(f\cdot g)(x;0)=\sum _{n=0}^{\infty }{\frac {1+n}{n!}}x^{n}.

Diese Taylorentwicklung wäre allerdings auch direkt über die Berechnung der Ableitungen von $\exp(x)\cdot (1+x)$ möglich:

{\begin{aligned}(\exp(x)\cdot (1+x))^{(n)}(x)&=\exp(x)\cdot (1+n+x)\\(\exp(x)\cdot (1+x))^{(n)}(0)&=1+n\end{aligned}}

Taylorreihen nichtanalytischer Funktionen

Dass die Taylorreihe an jeder Entwicklungsstelle $a$ einen positiven Konvergenzradius hat und in ihrem Konvergenzbereich mit $f$ übereinstimmt, gilt nicht für jede beliebig oft differenzierbare Funktion. Aber auch in den folgenden Fällen nichtanalytischer Funktionen wird die zugehörige Potenzreihe als Taylorreihe bezeichnet.

Konvergenzradius 0

Die Funktion

f(x)=\int _{0}^{\infty }{\frac {\mathrm {e} ^{-t}}{1+x^{2}t}}\mathrm {d} t

ist auf ganz $\mathbb {R}$ beliebig oft differenzierbar, aber ihre Taylorreihe in $a=0$ ist

Tf(x;0)=1-x^{2}+2!x^{4}-3!x^{6}+4!x^{8}\mp \dotsb

und somit nur für $x=0$ konvergent (nämlich gegen bzw. gleich 1).[1]

Eine Funktion, die in einer Entwicklungsstelle nicht in eine Taylorreihe entwickelt werden kann

Die Taylorreihe einer Funktion konvergiert nicht immer gegen die Funktion. Im folgenden Beispiel stimmt die Taylorreihe auf keiner Umgebung um die Entwicklungsstelle $a=0$ mit der Ausgangsfunktion überein:

f(x)={\begin{cases}0&{\text{für }}x\leq 0\\\mathrm {e} ^{-1/x^{2}}&{\text{für }}x>0\end{cases}}

Als reelle Funktion ist $f$ beliebig oft stetig differenzierbar, wobei die Ableitungen in jedem Punkt $x\leq 0$ (insbesondere für $x=0$ ) ausnahmslos 0 sind. Die Taylorreihe um den Nullpunkt ist also die Nullfunktion und stimmt in keiner Umgebung der 0 mit $f$ überein. Daher ist $f$ nicht analytisch. Die Taylorreihe um eine Entwicklungsstelle $a>0$ konvergiert zwischen $0$ und $2a$ gegen $f$ . Auch mit einer Laurentreihe lässt sich diese Funktion nicht approximieren, weil die Laurentreihe, die die Funktion für $x>0$ korrekt wiedergibt, für $x<0$ nicht konstant 0 ergibt.

Mehrdimensionale Taylorreihe

Sei nun im Folgenden $f\colon \mathbb {R} ^{d}\to \mathbb {R}$ eine beliebig oft stetig differenzierbare Funktion mit Entwicklungsstelle $a\in \mathbb {R} ^{d}$ .

Dann kann man zur Funktionsauswertung $f(x)$ eine mit $x$ und $a$ parametrisierte Familie von Funktionen $F_{x;a}(t)\colon \mathbb {R} \to \mathbb {R}$ einführen, die man so definiert:

F_{x;a}(t)=f(a+t\cdot (x-a))

$F_{x;a}(1)$ ist dann, wie man durch Einsetzen von $t=1$ feststellt, gleich $f(x)$ .

Berechnet man nun von $F_{x;a}$ die Taylorentwicklung am Entwicklungspunkt $t_{0}=0$ und wertet sie bei $t=1$ aus, so erhält man die mehrdimensionale Taylorentwicklung von $f$ :

Tf(x;a):=TF_{x;a}(1;0)=\sum _{n=0}^{\infty }{\frac {F_{x;a}^{(n)}(0)}{n!}}

Mit der mehrdimensionalen Kettenregel und den Multiindex-Notationen für $\alpha =(\alpha _{1},\dotsc ,\alpha _{d})\in \mathbb {N} _{0}^{d}$

D^{\alpha }={\frac {\partial ^{|\alpha |}}{\partial x_{1}^{\alpha _{1}}\cdots \partial x_{d}^{\alpha _{d}}}}\qquad {\binom {n}{\alpha }}={\frac {n!}{\prod _{i=1}^{d}\alpha _{i}!}}

erhält man ferner:

F_{x;a}^{(n)}(t)=\sum _{|\alpha |=n}{\binom {n}{\alpha }}(x-a)^{\alpha }D^{\alpha }f(a+t(x-a))

Mit der Schreibweise ${\displaystyle \alpha$ erhält man für die mehrdimensionale Taylorreihe bzgl. des Entwicklungspunktes $a$

{\displaystyle Tf(x;a)=\sum _{|\alpha |\geq 0}{\frac {(x-a)^{\alpha }}{\alpha

in Übereinstimmung zum eindimensionalen Fall, falls man die Multiindex-Notation verwendet.

Ausgeschrieben sieht die mehrdimensionale Taylorreihe wie folgt aus:

{\begin{aligned}Tf(x;a)=&\ \sum _{n_{1}=0}^{\infty }\cdots \sum _{n_{d}=0}^{\infty }{\frac {\prod _{i=1}^{d}(x_{i}-a_{i})^{n_{i}}}{\prod _{i=1}^{d}n_{i}!}}\,\left({\frac {\partial ^{\sum _{i=1}^{d}n_{i}}f}{\partial x_{1}^{n_{1}}\cdots \partial x_{d}^{n_{d}}}}\right)(a)=\\=&\ f(a)+\sum _{j=1}^{d}{\frac {\partial f(a)}{\partial x_{j}}}(x_{j}-a_{j})+{\frac {1}{2}}\sum _{j=1}^{d}\sum _{k=1}^{d}{\frac {\partial ^{2}f(a)}{\partial x_{j}\partial x_{k}}}(x_{j}-a_{j})(x_{k}-a_{k})+{}\\&+{\frac {1}{6}}\sum _{j=1}^{d}\sum _{k=1}^{d}\sum _{l=1}^{d}{\frac {\partial ^{3}f(a)}{\partial x_{j}\partial x_{k}\partial x_{l}}}(x_{j}-a_{j})(x_{k}-a_{k})(x_{l}-a_{l})+\dotsb \end{aligned}}

Beispiel

Zum Beispiel gilt nach dem Satz von Schwarz für die Taylorreihe einer Funktion $g\colon \mathbb {R} ^{2}\to \mathbb {R}$ , die von $x=(x_{1},x_{2})$ abhängt, an der Entwicklungsstelle $a=(a_{1},a_{2})$ :

{\begin{aligned}Tg(x;a)=&\ g(a)+g_{x_{1}}(a)\cdot (x_{1}-a_{1})+g_{x_{2}}(a)\cdot (x_{2}-a_{2})\ +\\&+{\frac {1}{2}}\left[(x_{1}-a_{1})^{2}g_{x_{1}x_{1}}(a)+2(x_{1}-a_{1})(x_{2}-a_{2})\,g_{x_{1}x_{2}}(a)+(x_{2}-a_{2})^{2}g_{x_{2}x_{2}}(a)\right]+\dotsb \end{aligned}}

Operatorform

Die Taylorreihe lässt sich auch in der Form $\mathrm {e} ^{(x-a)D}f(a)$ darstellen, wobei mit $D$ der gewöhnliche Ableitungsoperator gemeint ist. Der Operator $T^{h}$ mit $(T^{h}f)(x):=f(x+h)$ wird als Translationsoperator bezeichnet. Beschränkt man sich auf Funktionen, die global durch ihre Taylorreihe darstellbar sind, so gilt $T^{h}=\mathrm {e} ^{hD}$ . In diesem Fall gilt also

f(x+h)=\mathrm {e} ^{hD}f(x)=\sum _{k=0}^{\infty }{\frac {h^{k}}{k!}}D^{k}f(x).

Für Funktionen von mehreren Variablen lässt sich $hD$ durch die Richtungsableitung $D_{h}=\langle h,\nabla \rangle$ austauschen. Es ergibt sich

{\displaystyle f(x+h)=\mathrm {e} ^{\langle h,\nabla \rangle }f(x)=\sum _{k=0}^{\infty }{\frac {\langle h,\nabla \rangle ^{k}}{k!}}f(x)=\sum _{|\alpha |\geq 0}{\frac {h^{\alpha }}{\alpha

Man gelangt von links nach rechts, indem man zunächst die Exponentialreihe einsetzt, dann den Gradienten in kartesischen Koordinaten sowie das Standardskalarprodukt und schließlich das Multinomialtheorem verwendet.

Für die Taylorreihe lässt sich auch ein diskretes Analogon finden. Man definiert dazu den Differenzenoperator $\Delta _{a}$ durch $(\Delta _{a}f)(x):=f(x+a)-f(x)$ . Offensichtlich gilt nun $T^{a}=I+\Delta _{a}$ , wobei mit $I$ der Identitätsoperator gemeint ist. Potenziert man nun auf beiden Seiten mit $h$ und verwendet die binomische Reihe, so ergibt sich

T^{ah}=(I+\Delta _{a})^{h}=\sum _{k=0}^{\infty }{\binom {h}{k}}\Delta _{a}^{k}.

Man gelangt zur Formel

f(x+ah)=\sum _{k=0}^{\infty }{\binom {h}{k}}\Delta _{a}^{k}f(x)=\sum _{k=0}^{\infty }{\frac {h^{\underline {k}}}{k!}}\Delta _{a}^{k}f(x),

wobei mit $h^{\underline {k}}$ die absteigende Faktorielle gemeint ist. Diese Formel ist als newtonsche Formel zur Polynominterpolation bei äquidistanten Stützstellen bekannt. Sie stimmt für alle Polynomfunktionen, braucht aber für andere Funktionen nicht unbedingt korrekt zu sein.

Siehe auch

Linearisierung mittels Näherungswerten
Ausgleichsrechnung

Weblinks

Wikibooks: Taylorreihe mit Konvergenzradius Null – Lern- und Lehrmaterialien

Eric W. Weisstein: Taylor Series. In: MathWorld (englisch).

Einzelnachweise

Taylor-Reihe mit Konvergenzradius Null (Wikibooks).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Taylor-Reihe mit Konvergenzradius Null (Wikibooks).