Tarski-Gruppe

Eine Gruppe ${\displaystyle G}$ heißt Tarski-Gruppe, wenn gilt:

• ${\displaystyle G}$ ist unendlich,
• jede echte, nicht-triviale Untergruppe ist endlich von Primzahl-Ordnung.

Eine Gruppe ${\displaystyle G}$ heißt erweiterte Tarski-Gruppe, wenn es einen Normalteiler ${\displaystyle N\subset G}$ gibt, so dass gilt:

• Die Quotientengruppe ${\displaystyle G/N}$ ist eine Tarski-Gruppe,
• ${\displaystyle N}$ ist zyklisch von Primzahlpotenz-Ordnung > 1,
• für jede Untergruppe ${\displaystyle H\subset G}$ gilt ${\displaystyle H\subset N}$ oder ${\displaystyle N\subset H}$.[2]

Die Struktur des Untergruppenverbandes einer Tarski-Gruppe

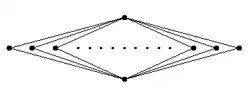
Alfred Tarski hatte die Frage aufgeworfen, ob es unendliche Gruppen gibt, deren Untergruppenverband die Höhe 2 hat,[3] das heißt wie nebenstehend aussieht. Die Existenz solcher Gruppen war lange unklar, schließlich zeigte Olschanski im Jahre 1979, dass es zu Primzahlen ${\displaystyle p>10^{75}}$ p-Gruppen dieser Art gibt.[4] Damit waren gleichzeitig weitere Gegenbeispiele zum beschränkten Burnside-Problem gefunden, das die Frage stellt, ob endlich erzeugte Gruppen mit einem endlichen Gruppenexponenten schon endlich sein müssen. Da Tarski-Gruppen von zwei Elementen erzeugt sind (siehe unten), hat man mit ihnen weitere Gegenbeispiele der gewünschten Art. Ferner folgt, dass es zu ${\displaystyle p=2}$ und ${\displaystyle p=3}$ keine Tarski-${\displaystyle p}$-Gruppen geben kann, denn sonst müssten die Burnside-Gruppen ${\displaystyle B(2,2)}$ bzw. ${\displaystyle B(2,3)}$ unendlich sein, was nicht der Fall ist.

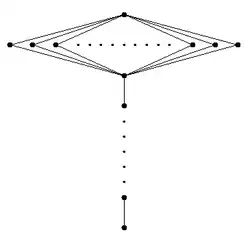
Die Struktur des Untergruppenverbandes einer erweiterten Tarski-Gruppe

Da je zwei verschiedene, echte Untergruppen ${\displaystyle U}$ und ${\displaystyle V}$ einer Tarski-Gruppe Primzahlordnung haben, muss ihr Durchschnitt ${\displaystyle U\cap V}$ trivial sein. Die von ihnen erzeugte Untergruppe ${\displaystyle \langle U\cup V\rangle }$ muss mit der Gesamtgruppe übereinstimmen, da anderenfalls ${\displaystyle \langle U\cup V\rangle }$ von Primzahlordnung wäre und ${\displaystyle U}$ und ${\displaystyle V}$ enthalten müsste, was zu ${\displaystyle U=\langle U\cup V\rangle =V}$ führte. Daher bilden die echten, nicht-trivialen Untergruppen einer Tarski-Gruppe eine Antikette.

Die Struktur des Untergruppenverbandes von Tarski-Gruppen und erweiterten Tarski-Gruppen sieht damit wie in nebenstehenden Skizzen aus, insbesondere handelt es sich um M-Gruppen.

Da Tarski-Gruppen nach Obigem von zwei Elementen erzeugt sind und daher erweiterte Tarski-Gruppen endlich erzeugt sind, können sie nicht lokalendlich sein. (Gruppen heißen lokal endlich, wenn jede endlich erzeugte Untergruppe endlich ist.)

Umgekehrt treten Tarski-Gruppen in unendlichen, von zwei Elementen erzeugten M-Gruppen wie folgt auf:

Es seien ${\displaystyle G}$ eine M-Gruppe und ${\displaystyle x,y\in G}$ zwei Elemente von Primzahlpotenz-Ordnung. Das Erzeugnis ${\displaystyle H:=\langle x,y\rangle }$ dieser beiden Elemente sei unendlich. Dann gilt:[5][6]

• Ist ${\displaystyle \langle x\rangle \cap \langle y\rangle =\{1\}}$, so ist ${\displaystyle H}$ eine Tarski-Gruppe.
• Ist ${\displaystyle \langle x\rangle \cap \langle y\rangle \not =\{1\}}$, so ist ${\displaystyle H}$ eine erweiterte Tarski-Gruppe.

Es ist klar, dass Tarski-Gruppen Torsionsgruppen sind, denn ist ${\displaystyle x}$ Element einer Tarski-Gruppe ${\displaystyle G}$, so ist die von ${\displaystyle x}$ erzeugte Untergruppe ${\displaystyle \langle x\rangle =\{x^{n}\mid n\in \mathbb {Z} \}}$ eine echte Untergruppe, andernfalls wäre ${\displaystyle G}$ zyklisch, also isomorph zu ${\displaystyle \mathbb {Z} }$, aber ${\displaystyle \mathbb {Z} }$ ist keine Tarski-Gruppe. Als echte Untergruppe einer Tarski-Gruppe muss ${\displaystyle \langle x\rangle }$ endlich sein, das heißt, ${\displaystyle G}$ ist eine Torsionsgruppe. Daraus erhält man leicht, dass auch erweiterte Tarski-Gruppen Torsionsgruppen sind. Bei der Beschreibung des Untergruppenverbandes wurde bereits festgestellt, dass es sich um M-Gruppen handelt.

Umgekehrt treten Tarski-Gruppen und erweiterte Tarski-Gruppen nach einem Satz von R. Schmidt wie folgt als Bestandteile solcher Gruppen auf:[7][8][9]

Eine Torsionsgruppe ist genau dann eine M-Gruppe, wenn sie das direkte Produkt von

• Tarski-Gruppen,
• erweiterten Tarski-Gruppen
• und einer lokalendlichen Gruppe,

ist, so dass je zwei Elemente aus verschiedenen direkten Faktoren teilerfremde Ordnungen haben.

Tarski-Gruppen sind einfach.[10] Sei nämlich ${\displaystyle N}$ ein nicht-trivialer Normalteiler der Tarski-Gruppe ${\displaystyle G}$. Dann ist ${\displaystyle N}$ endlich und daher ${\displaystyle G/N}$ unendlich. Ein vom Einselement verschiedenes Element in ${\displaystyle G/N}$ hat endliche Ordnung und erzeugt daher eine echte, nicht-triviale Untergruppe in ${\displaystyle G/N}$. Ihr Urbild unter der Quotientenabbildung ist dann eine Untergruppe, die echt zwischen ${\displaystyle N}$ und ${\displaystyle G}$ liegt. Diese muss endlich von Primzahlordnung sein und mit ${\displaystyle N}$ eine echte Untergruppe enthalten. Dieser Widerspruch zeigt, dass ${\displaystyle N}$ kein Normalteiler sein kann, das heißt, ${\displaystyle G}$ ist einfach.

1. L. N. Shevrin, A. J. Ovsyannikov: Semigroups and their Subsemigroup Lattices, Springer-Verlag, 1996, ISBN 978-94-015-8751-8, Kapitel 5.13
2. Roland Schmidt: Subgroup Lattices of Groups, Walter de Gruyter (1994), ISBN 3-11-011213-2, Seite 82: Torsion groups with modular subgroup lattices
3. B. H. Neumann: Some new rumors in group theory, Math. Medley 6 (3), Seiten 100–103
4. A. Yu. Olshanskii: Infinite groups with cyclic subgroups, Dokl. Akad. Nauk SSSR, 245:4 (1979), 785–787
5. Roland Schmidt: Subgroup Lattices of Groups, Walter de Gruyter (1994), ISBN 3-11-011213-2, Lemma 2.4.17
6. Ragmar Rudolph: Ein Untergruppensatz für modulare Gruppen, Monatshefte für Mathematik, Band 94 (1982), Seiten 149–153
7. P. Pálfy: Groups and Lattices in Groups St Andrews 2001 in Oxford, London Mathematical Society, Lecture Notes Series 305, Band II, Cambridge University Press (2003), ISBN 0-521-53740-1, Seite 432, Theorem 2.5
8. Roland Schmidt: Subgroup Lattices of Groups, Walter de Gruyter (1994), ISBN 3-11-011213-2, Theorem 2.4.16
9. Roland Schmidt: Gruppen mit modularem Untergruppenverband, Arch. Math 46, Seiten 118–124 (1986)
10. D. J. S. Robinson: A Course in the Theory of Groups, Springer-Verlag 1996, ISBN 0-387-94461-3, Kapitel 14.4, Aufgabe 1